通信设备检测时性能测试标准值的确定模型与算法

徐济仁， 陈家松， 朱锦山， 王可人

（①合肥工业大学，安徽 合肥 230000；②电子工程学院，安徽 合肥 230037；③73676部队，江苏 无锡 214063）

0 引言

通信设备的日常检测是使用单位日常维护与保养的重要内容之一，按时间周期来划分，通常有月检测、季检测和年检测。检测的内容通过有一般检查、功能检查和性能测试。一般检查主要包括包括外观检查和供电检测，功能检查主要是对通信设备一些基本的功能进行快速的检查，大致了解设备的工作情况。而性能测试则是全面了解设备的工作情况，通过对设备主要性能指标的测试，了解当前设备的主要性能指标，通过对指标的分析，判断通信设备是否能够正常使用[1]。

性能测试程序应规范，测试用的性能指标应能反应设备的工作状态。

通信设备的主要性能指标测试完成之后，根据什么标准来判断当前设备是否能够正常使用呢？显然，我们不能用该通信设备的出厂指标。因为，通信设备便用一段时间以后，反映设备工作状态的主要性能指标大多数会下降。根据我们多年来对设备的维护与保养的经验，性能指标使用一段时间以后，都会出现不同程度的下降，有的指标下降得快一些，有的指下降得慢一些。如最能反映通信设备指标的灵敏度下降比较明显。

理论分析与实践经验表明，在通信设备正常的条件下，通信设备的性能指标通过按常某一指数曲线衰减，即：

其中：S0为通信设备的出厂指标；T为设备的便用时间；σ为衰减因子，对于不同的性能指标值，σ应取不同的值；S为通信设备使用一波时间以后的性能指标，它是一个计算值，也是一个预测值。如果设备工作正常，就应该符合这个值，所以，通过我们也称之为测试标准值；如果测试的性能指标就会和公式（1）预测的指标相差较大，就表明通信设备工作不正常，如设备出现程度不等的却又不明显影响使用的故障、违规、超常使用等，从而发现有潜在故障的通信设备，或指标存在隐患的设备[2]。及时发现问题加以纠正，这也是我们设备检测的重任务和内容之一。

1 检测标准值的计算方法

从式（1）中可以发现，如果知道 S0和 σ，那么就可以使用式（1）。二个未知数至少需要二次检测值。另外，考虑到设备性能下降，指标值可出现变大，也有可能变小。同时，设备也可能经过大修或中修。综合起来考虑，我们将通信设备检测标准值的计算方法归纳如下：

检测标准值的计算方法如下：

（1）分别用式(2)、式(3)计算各测试项目的允许变化值、检测标准值，填写表1中。

式中：Δs为测试项目的允许变化值。当指标下降时，测试指标值变大，Δs取正，否则取负；s0为设备出厂的检测结果(便用单位可能没有这个结果，但是可以用式(6)推算得到)；λ为等效使用时间的修正系数。

式中：s为测试项目的本次检测标准值。

（2）等效使用时间的修正系数λ按式(4)计算：

式中：m为修正因子。设备正常使用时，m取0；如果设备经过大修，则m取－0.00995；如果设备经过中修，则m取－0.00329；σ为衰减因子；T为等效使用时间。

2 前二次检测结果用于确定参数s0和σ

假设首次检测和第二次检测的结果分别为s1、s2，等效使用时间分别为T1、T2，则：

等效使用时间T1、T2的计算方法参见GJB 5396—2005中的附录A。

设备经过大修或中修后应重新进行首次检测和第二次检测，得到s1、s2后，再次计算s0和σ。

3 举例

某通信设备正常使用了2.4年后，进行首次检测，设备正常使用了3.6年后，进行第二次检测。

以动态范围为例，假设首次检测值为49.49 dB，第二次检测值为 49.23 dB，按式(5) ,式(6)得到σ=0.9957，s0=50 dB。

现在该设备正常使用了4.8年，准备进行第三次检测，m取0，按式(4)等效使用时间的修正系数λ=0.0205。

按式(2)瞬时动态范围的允许变化值Δs=－1.025 dB，按式(3)动态范围的本次检测标准值s=48.98 dB。

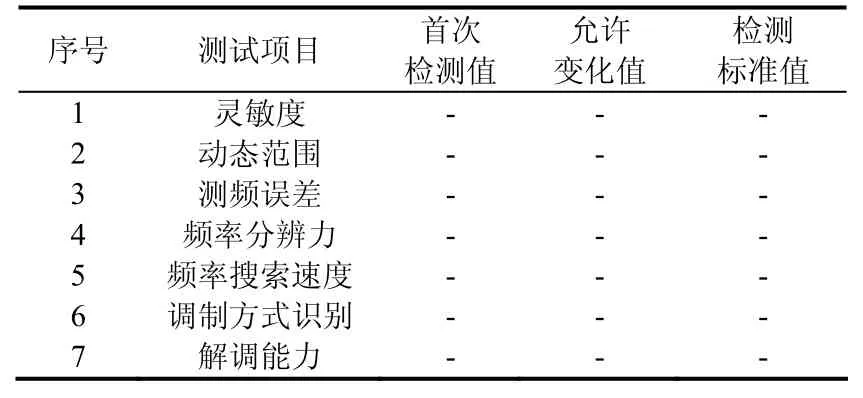
表1 测试项目的允许变化值和检测标准值

4 三次以上检测结果时参数s0和σ确定方法

如果有三次以上的检测结果，显然不能用式（5）,式（6）来计算，我们可以用最小二乘的方法来确定，令：

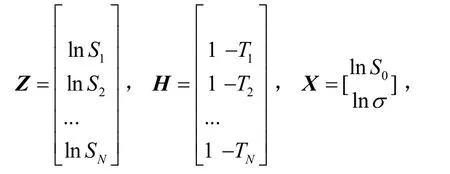
则：X的无偏估计值为：

这就是人们熟知的最小二乘估计[3-4]。

从式（7）的计算中，我们可以发现，有大量的矩阵运算和求导运算，而且如果再增加一次检测数据，又需要一次重新计算。能不能采用其它的方法呢？下面是作者首次尝试将递推最小二乘方法用于检测标准值的计算方法的算法，对于提高检测标准值的计算精度和简化运算量有一定的作用。

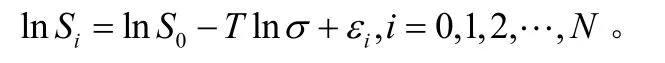
对式（1）取对数，由此我们得到观测模型为：

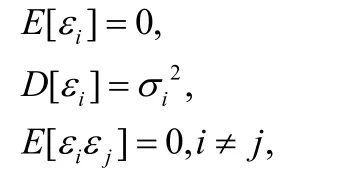
且记

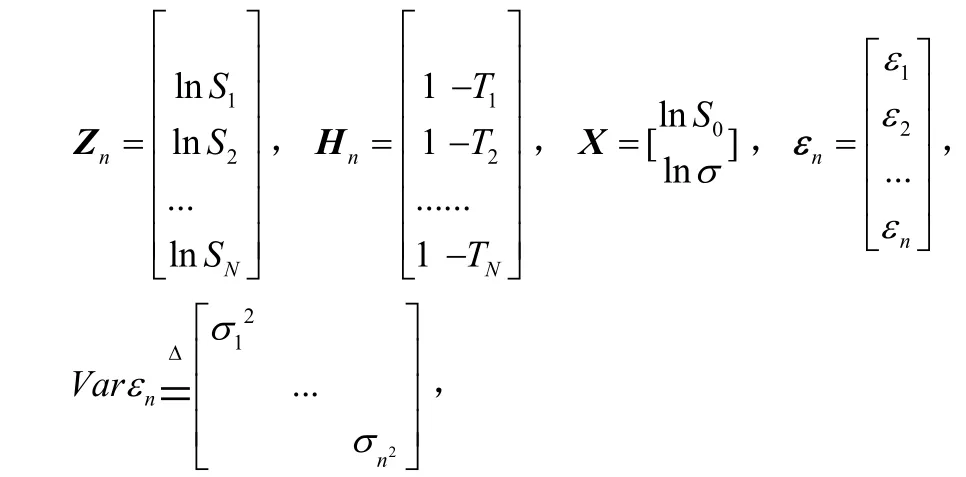
于是：Zn= HnX +εn,zn+1= xic tgφi- yi= xTctgφi- yT+εn+1，

这时假设又得到了下一个的检测数据，此时我们获得了Zn+1,且

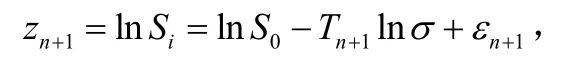
记 Mn+1= [1 -Tn+1]，

可以得到：

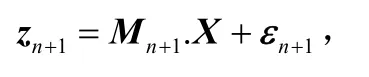
在得到了n+1个检测数据后，X的估计值Xn+1为：

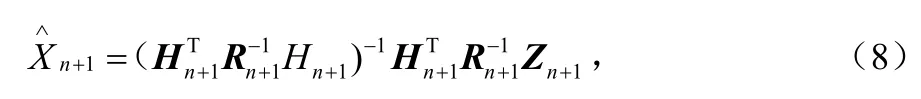
其中：

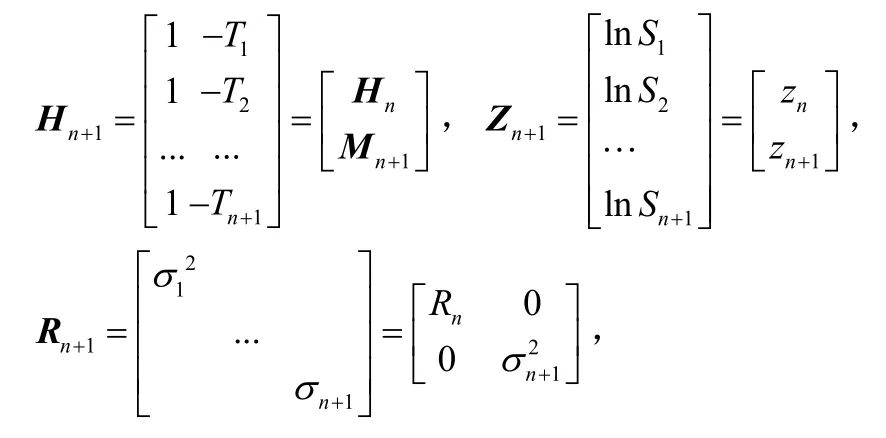
将上述矩阵和向量的分块表示式代入式（1），最后得到：

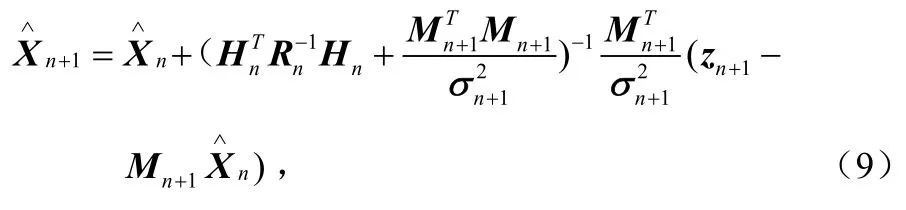
不加证明地给出引理1：

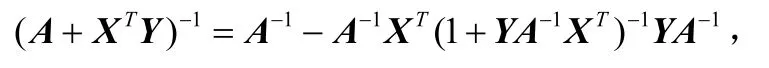
其中A为方阵，X，Y为行矢量。

运用引理1，式（8）还可以进一步简化为：

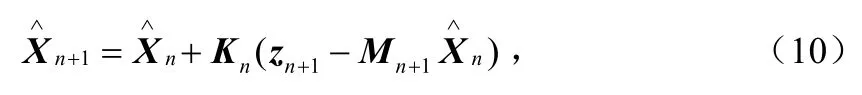
证明如下：在公式(1b)中，记

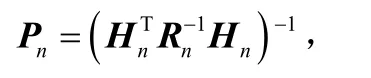
则：

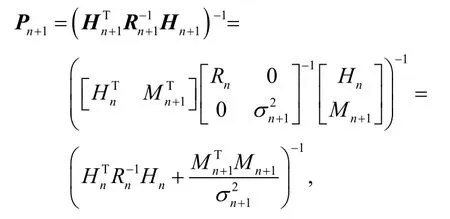
应用距阵求逆引理[5-6]，得：

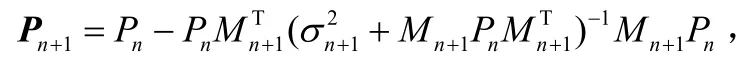
而

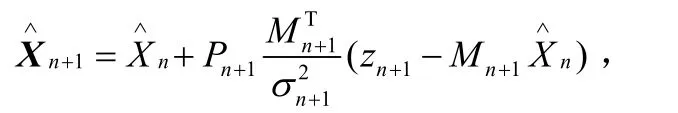
将Pn+1的表达式代入上式之则它可表示为

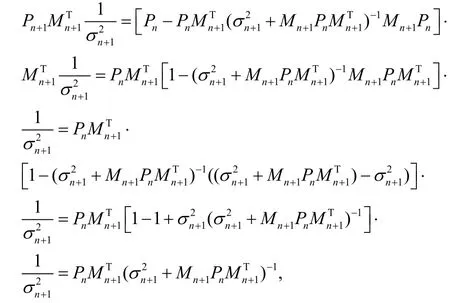
于是：

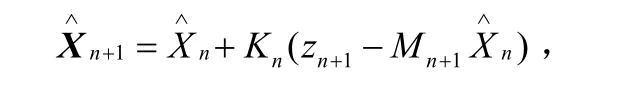
其中：

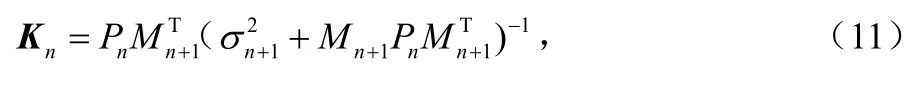
而

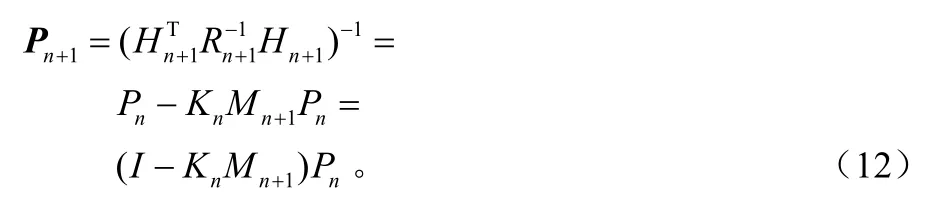
公式（11）～（12）的计算结构图如图1所示。

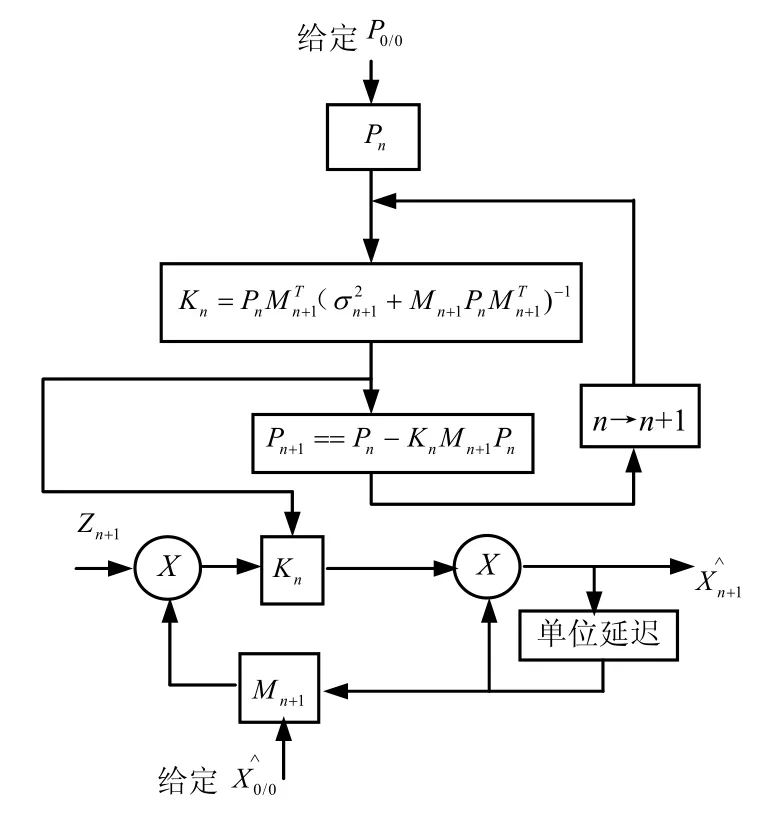
图1 递推最小二乘方法用于检测标准值的计算方框

① 当在时刻 tn已经算好了 和 Pn之后，那么应用式(10)～(12)可以非常方便地获得 和Pn+1；而且注意到式（11）右端出现的（ ）-1，它并不是矩阵的求逆，而不过是一个普通的倒数；这就避免了式（9）中的矩阵的求逆运算；

② 递推运算中，必须首先给出初始运算条件 及 P0，可以应用式（7）直接求出。

实际检测中，当我们已经获得n了个检测数据，如果这时再增加一个检测数据时，就可运用上述公式来进一步提高检测的精度，而且可以大大简化运算量。

[1] 杨成.基于虚拟仪器的航空电子设备检测系统设计[J].指挥控制与仿真,2008(03):56-58.

[2] 张扬,陈鲁汉,宁波.基于 1553B总线的航空电子设备的检测系统设计[J].电子测量技术,2008(04):45-47.

[3] Rhea, Randall W. Oscillation Design and Computer Simulation[M].Second Edition. Ailanta:Noble Publishing, 1995:73-78.

[4] Ross W. The Estimation of the Probable Accuracy of High-Frequency Radio Direction-Finding Bearings [J].Journal IEEE,1947,94(Part Ⅲ A):722-725.

[5] Wiley R G. Electronic Intelligence: the Interception of Radar Signals[J].Norwood, MA :Artech House, 1985:110-112.

[6] Torrieri D J. Statistical Theory of Passive Location Systems[J].IEEE Trans. Aerospace and Electronic Systems,1984,AES-20(02):183-198.