基于量子粒子群优化算法的图像分割方法*
黄洋文,王红亮
(中北大学 电子测试技术国家重点实验室;仪器科学与动态测试教育部重点实验室,山西 太原 030051)
1 引言
图像分割是图像识别和图像理解的基础。所谓图像分割就是将图像依据一定的准则划分为目标部分(人们感兴趣的特征部分)和背景部分。目前,图像分割方法主要有阈值法、聚类法、边缘检测法等[1-4]。其中阈值法由于其简单性和有效性从而得到广泛的应用。目前已提出的阈值法有Otsu法、最大熵法、Fisher准则函数法、迭代分割法以及这些方法在基于二维直方图上的推广等。著名的Otsu法通过最大化图像中目标和背景的类间方差来选取最佳阈值,方法简单,且对大部分图像分割效果较好;缺点是在图像信噪比较低或目标太小的情况下分割效果不佳。最大熵法通过最大化图像中目标与背景分布的信息量来选取最佳阈值选;缺点是在图像中目标和背景对比度较小情况下会造成明显错分类[1]。基于一维Fisher准则函数的分割算法受目标和背景的比例影响小,能有效识别出与背景比例悬殊的小目标,分割精度高[2]。由于二维直方图在一维直方图的基础上增加了对图像中各像素点邻域的描述,基于二维直方图的图像分割算法效果会更好。文献[5]提出了二维Fisher准则函数算法。该算法受目标和背景比例影响小,具有很好的应用价值,但存在效率低的缺点,需要选择一种优化算法求得最佳阈值,来减少运算时间。
粒子群优化(Particle Swarm Optimization,PSO)算法是一种基于种群搜索的智能计算方法。量子粒子群优化算法(Quantum Particle Swarm Optimization,QPSO)[6]是把量子理论应用于PSO算法而提出的改进的粒子群优化算法,较PSO算法更加简单、易实现,且收敛速度更快。
笔者将二维Fisher准则函数和量子粒子群优化算法相结合应用于图像分割,并针对量子粒子群优化算法存在收敛性差、易早熟的问题,对量子粒子群优化算法进行改进,取得了很好的实验效果。
2 量子粒子群优化算法
由于粒子群优化算法存在早熟趋势,不能保证以概率1搜索到全局最优解,许多学者采用各种方法来解决这一问题。2004年Sun等从量子力学的角度提出了一种新的粒子群优化算法模型[6-7]。它通过量子态来描述粒子,使得算法可以在整个可行解空间中进行搜索,大大提高了算法的全局搜索能力。该算法主要可以描述为:在量子空间中,粒子的速度和位置是不能同时确定的,粒子的状态通过波函数ψ(x,t)来描述,并通过求解薛定谔方程得到粒子在空间某一点出现的概率密度函数[8]。随后通过蒙特卡罗随机模拟的方式得到粒子的位置方程。主要迭代公式有
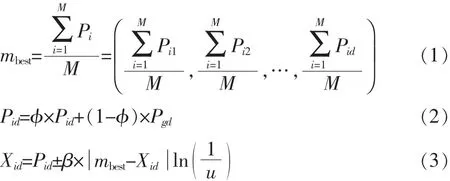
式中:φ和u为[0,1]范围内的随机数。β为收缩扩张系数,它是量子粒子群优化算法中的一个重要参数,第T次迭代时一般可取 β=0.5+0.5×(Tmax-T)/Tmax;Tmax为最大迭代次数。
3 改进算法
3.1 二维Fisher准则函数算法原理
设图像灰度级为L,定义pij为灰度为i且其邻域灰度均值为j的像素的发生概率,将pij分别向i,j两个坐标轴投影,分别用 H(i)和 W(j)表示,则
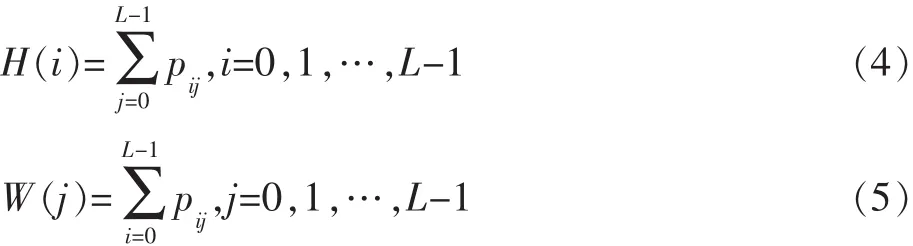
定义(μ0i,μ0j)和(μ1i,μ1j)分别表示 ω1(背景类)和 ω2(目标类)在 i,j坐标轴上投影的均值,分别表示ω1和ω2在i,j坐标轴上投影的方差,则根据Fisher准则函数的定义,可以推导出图像分割的二维Fisher准则函数为
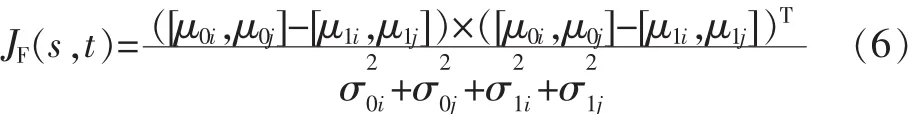
在二维直方图上选择不同的(s,t),当 JF(s,t)最大时,即为最佳分割阈值[9]。
3.2 基于QPSO的二维Fisher准则函数算法
以二维Fisher准则函数作为量子粒子群优化算法的适应度函数,根据它的大小选择个体极值和全体极值,不断地更新粒子,最终求得全局最大值及其对应的粒子位置。具体的流程如下:
1)粒子群规模为N,随机对微粒群各微粒的初始位置(256级灰度中的某个灰度值)进行设定。
2)利用式(6)计算每个粒子的适应度,同时根据适应值选取每个粒子的个体最优Pid以及粒子群的全体最优Pgd。
3)计算式(1),(2)和(3)以更新粒子的位置,同时利用式(6)计算适应度。对每个粒子,比较其适应度与个体最优Pid的适应度,若较大,则将其作为个体最优Pid;对每个粒子,比较其个体最优Pid的适应度与全体最优Pgd的适应度,若较大,则将其作为全体最优Pgd。
4)如果全体最优Pgd在一定的迭代次数内变化都小于所设定的允许误差或者总迭代次数超过所设定的最大值,则算法结束,全体最优Pgd对应的就是最佳阈值;否则转到步骤3)继续迭代。
5)利用所得到的最佳阈值对各像素点进行分类。
3.3 改进的算法
虽然量子粒子群优化算法比粒子群优化算法具有更强的全局搜索能力,但它仍存在一定的早熟趋势;文献[10]采用多样性控制模型来解决这一问题,但多样性控制模型的部分参数无法自动设定到最佳值,这使得该算法的应用受到了限制;而且该算法以增加迭代次数为代价,降低了收敛速度。针对其不足,提出了量子粒子群优化算法和邻域搜索双重寻优的改进算法。改进后的算法流程为:
1)将粒子群各微粒的初始位置进行平均分布。定义待分割图像中出现的最大像素值为Imax,最小像素值为Imin,粒子群规模为N,则粒子群第i个微粒的初始位置由下式计算得到
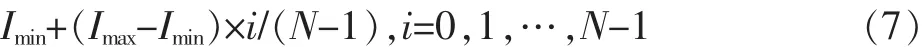
2)利用量子粒子群优化算法进行快速粗略寻优。可以通过适当地缩小粒子群规模和降低终止条件的要求来快速求得次优值Jgd及其对应的粒子位置Pgd。
3)通过邻域搜索,查找最优值。定义n为邻域搜索有效步数,N为邻域搜索最大有效步数。它主要包括以下几步:
(1)求Pgd的右邻位置Pgd+1对应的适应值Jgd+1,求Pgd的左邻位置Pgd-1对应的适应值Jgd-1,进行如下的双邻搜索(包括右邻搜索和左邻搜索)。
(2)右邻搜索:若在右邻位置寻得更优值,即Jgd+1>Jgd,则终止左邻搜索,并令 Jgd=Jgd+1,Pgd=Pgd+1,n=0。然后继续右邻搜索。若Jgd+1<Jgd,则n=n+1,然后将Pgd+2作为新的右邻,继续右邻搜索。
(3)左邻搜索:若在左邻位置寻得更优值,即Jgd-1>Jgd,则终止右邻搜索,并令 Jgd=Jgd-1,Pgd=Pgd-1,n=0。 然后继续左邻搜索。 若 Jgd-1<Jgd,则 n=n+1,然后将 Pgd-2作为新的左邻,继续左邻搜索。
(4)依次搜索,当连续N次邻域搜索都无更优值时,即n≥N,终止搜索。此时的Jgd为最优值,Pgd为最优位置。
4 实验结果和分析
为了验证算法的有效性,在Petium 2.5 GHz的PC上,利用VC++6.0编写代码实现二维Otsu法、二维Fisher准则函数算法、基于量子粒子群优化算法的二维Fisher准则函数算法和本文算法等3种算法,并做了大量实验,总结如下:
1)实验对象为256级的灰度图像。两种算法的部分参数作如下设定:基于量子粒子群优化算法的二维Fisher准则函数算法的粒子群规模设定为10,终止条件为全体最优Pgd在连续3次迭代内无变化或总迭代次数达到20次。本文算法的粒子群规模设定为5,量子粒子群优化算法的终止条件为全体最优Pgd在连续1次迭代内无变化或总迭代次数达到20次。邻域搜索最大有效步数N设定为2。
2)选用一幅经过滤波和增强的红外图像作为实验对象,如图1所示。

图1 两种算法分割效果图
图1b中的错分点明显多于图1c的错分点,可见在分割效果上二维Fisher准则函数算法优于二维Otsu法。这主要是因为前者不仅考虑了目标和背景的类间方法最大,还考虑了目标和背景的类内方差最小,更不易受目标和背景的比例影响,分割精度更高。
3)选取3幅经过滤波和增强的红外图像作为实验对象,对每幅图像进行10次实验。对于二维Fisher准则函数,分别采用二维Fisher准则函数算法(穷举法)、基于量子粒子群优化算法的二维Fisher准则函数算法(QPSO)和本文算法求得最大值,结果见表1,其中的达优数是指运行结果和穷举法结果相同的次数。
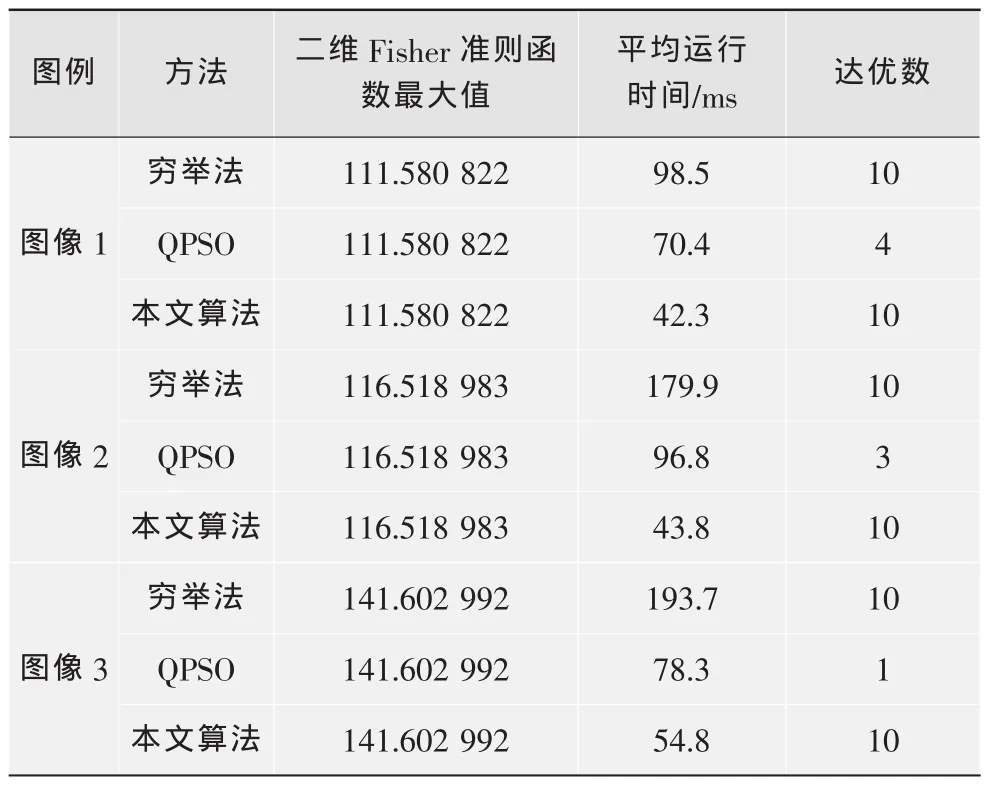
表1 3种算法图像分割结果分析
从表1可以看出,在相同条件下分割3幅图像,QPSO的计算总时间约为穷举法的52.0%,而本文算法的计算总时间约为穷举法的29.8%。这说明QPSO和本文算法都可以有效提高分割速度,且本文算法速度更快。另外,本文算法的达优率为100%,而QPSO的平均达优率仅为26.7%。这说明本文算法可以有效避免QPSO早熟,提高了全局搜索能力,保证了算法的稳定性和计算精度。
5 小结
二维Fisher准则函数算法是一种有效的图像分割方法,它结合了二维直方图和Fisher准则函数的优点,既考虑样本类内和类间离散度,又考虑像素间的空间邻域信息。在对低信噪比图像和小目标分割时效果优于二维Otsu法。而量子粒子群优化算法是一种参数简洁、流程简单易实现、收敛速度快的群体智能算法。因此,利用量子粒子群优化算法对二维Fisher准则函数进行快速寻优具有重要意义。但由于量子粒子群优化算法存在收敛性差、易早熟的问题,限制了它的应用。而笔者针对这一不足,对量子粒子群优化算法进行了改进,提出利用量子粒子群优化算法和邻域搜索法进行双重寻优。实验证明,改进后的分割方法能够取得很好的分割效果和计算速度,有效并且实用。
[1]张莎莎,谷延锋,张钧萍,等.一种基于量子遗传算法的红外图像分割方法[J].哈尔滨工业大学学报,2007,39(9):1427-1428.
[2]陈果.图像阈值分割的Fisher准则函数法[J].仪器仪表学报,2003,24(6):564-567.
[3]杨润玲,周军妮,刘利.基于改进型FCM聚类的图像分割新方法[J].电视技术,2008,32(6):12-14.
[4]曹世康,郭宝龙,符祥.基于时空信息融合的视频对象分割系统[J].电视技术,2007,31(1):17-19.
[5]童莹,邱晓晖.基于Fisher准则函数的二维阈值图像分割算法[J].电力系统通信,2004(9):36-39.
[6]SUN Jun,FENG Bin,XU Wen-bo.Particle swarm optimization with particles having quantum behavior[C]//Proc.Congress on Evolutionary Computation.[S.l.]:IEEE Press,2004:325-331.
[7]SUN J,XU W B.A global search strategy of quantum-behaved particle swarm optimization[C]//Proc.IEEE Conference on Cybernetics and Intelligent Systems.Singapore:IEEE Press,2004:111-116.
[8]汪筱红.基于QPSO的图像分割算法[J].合肥工业大学学报,2008,31(7):1088-1091.
[9]张怀柱,向长波,宋建中.改进的遗传算法在实时图像分割中的应用[J].光学精密工程,2008,16(2):333-335.
[10]孔丽丹,孙俊,须文波.基于全局层次的自适应QPSO算法[J].计算机工程与应用,2007,43(26):50-53.

