基于 ABAQUS的混凝土梁受弯破坏实验非线性分析

王 丽 邓思华

(北京建筑工程学院,北京 100044)

1 前言

随着有限元理论和计算机技术的不断发展,有限元分析软件的发展也日趋成熟,ABAQUS作为其中一种大型通用有限元分析软件在科研工作和实际工程中的应用也越来越普遍,因为它不仅具备其它有限元分析软件的数值计算快、结果精度高以及分析成本低等优点,还具有更人性化的操作界面和可视化结果,尤其是运用于钢筋混凝土结构非线性分析中能得到更精确的、更贴合实际的结果[1]。

2 ABAQUS钢筋混凝土非线性分析

钢筋混凝土结构非线性来源主要分为三类[2]:材料非线性、几何非线性、边界条件非线性。材料非线性是指钢筋和混凝土两种材料在结构受力分析过程中,不仅要考虑其弹性性能即线性阶段,也要考虑其塑性性能即非线性阶段。在 ABAQUS中是通过分别定义钢筋和混凝土的本构模型来实现其材料非线性的特性,弹性阶段须分别输入两种材料的弹性模量和泊松比;塑性阶段的定义则不同,钢筋只需输入其塑性阶段应力应变关系,而混凝土塑性有三种模型可以选择[3],包括有 Concrete Smeared Cracking(弥散裂纹混凝土模型)、Concrete Damaged Plasticity(混凝土损伤塑性模型)以及ABAQUS/Explicit中的 Cracking model for concrete(混凝土裂缝模型),其中混凝土损伤塑性模型具有一定的优越性,它可用于单项加载、循环加载以及动态加载等场合,且具有较好的收敛性,因此一般采用混凝土损伤塑性模型进行混凝土塑性定义。

边界条件在分析过程中发生变化就会产生边界非线性问题,包括构件之间的接触也属于边界条件的定义范畴。其中钢筋与混凝土的摩擦接触在ABAQUS中是通过 Embedded技术将钢筋单元埋入混凝土单元中来实现的[4]。

几何非线性发生在位移的大小影响到结构响应的情况下,只需要在 STEP选项中加入 NLGEOM参数即可,但一般静力非线性分析不需要选 NLGEOM参数,以免造成冗繁的计算量。

3 钢筋混凝土简支梁分析实例

3.1 模型建立

该简支梁长 1500 mm,截面尺寸为 180 mm×100mm,混凝土强度等级为 C25,纵筋和箍筋均采用HPB235钢筋,具体情况见图1。建立 ABAQUS模型混凝土采用 C3D8R单元,钢筋采用 T3D2单元,将钢筋埋入(Embedded)混凝土单元中来模拟钢筋混凝土之间的粘结关系。为防止加载过程中梁上加载面及支座处出现应力集中,因此建模时在梁加载处和支座处设置钢垫片,以增加接触面积和刚度,模型图如图2所示。

图1 简支梁配筋图

图2 简支梁模型图

3.2 钢筋混凝土相关参数计算

钢筋本构模型采用双直线模型,上升段的斜率为钢筋的弹性模量即 Es=210GPa,屈服应力 fy=210MPa,对应屈服应变为 0.001,水平段钢筋应力不变,钢筋破坏时应变为 0.006。混凝土弹性模量 Es=28GPa,混凝土单向受压本构模型采用美国 E.Hognestad[5]建议的模型计算公式:

其中,混凝土单轴抗压强度fc=11.9 MPa,屈服应变 ε0=0.002,极限应变 εu=0.0038。

混凝土单向受拉本构模型采用《钢筋混凝土结构设计规范》[6]中计算公式:

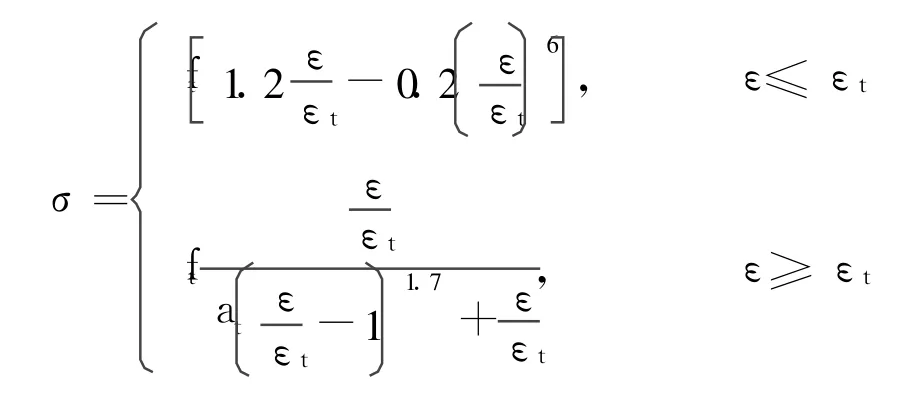
其中,混凝土单轴抗拉强度 ft=1.27MPa,混凝土峰值拉应变 εt=73.64×10-6。

3.3 分析结果

钢筋混凝土简支梁模型垫片上施加均布荷载3.2MPa(计算得 P=16 KN),分析得 Mises应力如图2所示。Mises应力最大值 41.16 MPa出现在支座垫板上,施加荷载垫板周围也存在较大应力,应力值在 3 MPa～14 MPa之间,并从加载垫板处向支座方向由大到小变化,从而两支座之间形成应力供体,值由小到大交替变化,形成传力途径,这与传统理论中有腹筋梁拱形桁架受力模型相类似。由于梁的肩部受力小,因此 Mises应力值较小,在受拉筋作用下梁的底部 Mises应力值也较小。

在加载垫片上施加均布荷载 3.2 MPa(计算得P=16 KN)得简支梁跨中节点的位移为 2.210 mm(见图4),其时间变化图如图5所示。可以看出,随分析计算时间的增加,跨中挠度增长速度逐渐加快,这是由于钢筋混凝土材料在弹性阶段强度大、刚度强,因此梁刚承受荷载时跨中挠度变化量小;而进入塑性阶段以后,钢筋混凝土材料性能下降,梁受力后挠度增加速度随之加快,从而形成跨中的挠度加速变化的曲线。由此看出此次模拟分析具有可靠的理论依据,是非常可信的。

图3 简支梁应力图

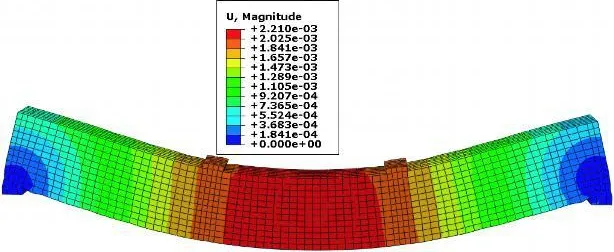
图4 简支梁位移图

图5 跨中位移 -时间图

4 小梁试验

经设计计算确定一个钢筋混凝土适筋梁的正截面尺寸、采用材料参数、配筋量等数据,实施两端简支、两点加载,试验模型如图1所示。试验时按计算承载力分级加载,两点加载值 P相同,控制加载速度,使用百分表和位移计量测钢筋混凝土梁的挠度,并记录对应荷载,同时观察梁的裂缝及破坏情况,加载至钢筋混凝土梁完全破坏为止。整理试验数据后绘制简支梁荷载 -挠度曲线如图6所示。

5 结果比较

为方便进行数值模拟和试验结果的分析比较,改变对简支梁的施加荷载,使用 ABAQUS软件重新计算分析,得出跨中节点的挠度值数据,将其与试验结果比较绘制出荷载 -挠度曲线如图7所示。

图6 荷载 -挠度曲线

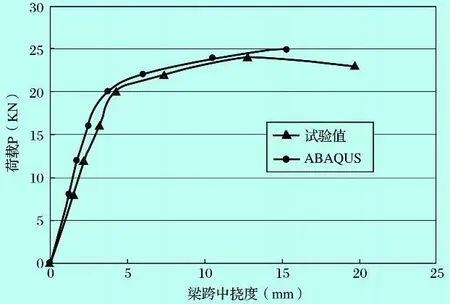
图7 简支梁跨中挠度值比较图

由上图看出,ABAQUS有限元分析的跨中挠度随荷载变化的趋势与试验结果相同,在荷载值 P达到 8 KN前,构件处于弹性阶段,其刚度、强度大,荷载值与挠度值基本成线性变化;之后构件进入塑性阶段,挠度增加值加快,当达到极限承载力 24 KN时,ABAQUS有限元分析计算得跨中挠度为10.521 mm,试验结果为 12.795 mm;最后梁屈服,挠度值增加进一步加快。可以看出 ABAQUS有限元分析能够得到与实际试验基本相符的结果,但两种方法计算的数值之间存在差异,经分析,原因可能有以下几点:

(1)模拟中有限元单元假设具有均匀、各向同性、单元间接触形式统一的特点[7],而实际混凝土构件材料构成复杂,有水泥等细小颗粒,也有砾石、细沙等构成成分,其相互之间的接触摩擦作用大不相同,另外各种材料性能各不相同,取用统一综合标准进行定义本身与实际就存在差异。

(2)有限元分析中混凝土与钢筋之间的粘结是采用 Embedded技术处理的,该方法有效简化了建模[8],但无法实现随荷载的增加混凝土与钢筋的摩擦时刻变化的特性,尤其是钢筋滑移的模拟难度很大等,容易导致结果失真。

(3)其他一些因素也会影响分析结果,比如:有限元分析的收敛性、模拟中参数取值的合理性、有限元单元的划分形式和数量、试验中试件浇筑质量及加载情况等。

总之,ABAQUS有限元分析模拟试验具有较高的相似度,虽有一些差异,但用 ABAQUS有限元方法针对小梁试验进行非线性分析是切实可行的。

6 结束语

本文通过使用 ABAQUS有限元软件模拟小梁试验,采用了混凝土损伤塑性模型以及钢筋与混凝土的 Embedded粘结技术,介绍了采用的钢筋与混凝土材料的本构模型,得到了与试验结果相近的分析结果,并探讨了结果产生差异的原因,证明了用ABAQUS有限元分析钢筋混凝土结构非线性问题是十分有效的,但如何能得到更精确的结果,仍需作更深入的研究。本文得到了北京市教委面上项目的资助。

[1]刘劲松,刘红军,ABAQUS钢筋混凝土有限元分析,装备制造技术,2009.6

[2]吕西林,金国芳,吴晓涵,钢筋混凝土结构非线性理论与应用[M],同济大学出版,1997.

[3]庄茁,张帆,岑松,ABAQUS非线性有限元分析与实例,科学出版社,2005

[4]ABAQUSAnalysis User's Manual,ABAQUS Inc,2006

[5]东南大学等,混凝土结构设计原理,中国建筑工业出版社,2008.6

[6]《混凝土结构设计规范》(GB50010-2002)

[7]江见鲸,陆新征,叶列平,混凝土结构有限元分析,清华大学出版社,2005

[8]张国丽,苏军,基于 ABAQUS的钢筋混凝土非线性分析,科学技术与工程,2008.10