不同相位噪声谱对QPSK的性能影响分析
胡 凡, 朱立东
(电子科技大学 通信抗干扰技术国家级重点实验室,四川 成都 610054)
0 引言
相位噪声是指单位Hz的噪声功率与信号总功率之比,是对信号时序变化的另一种测量方式,其结果在频率域内显示。相位噪声通常用噪声功率谱密度来描述,定义为某一频偏处的相位噪声功率与信号的总功率之比。
QPSK是一种恒包络调制方式,它受发射机功率放大器的非线性影响很小。Pawula对高斯扰动下夹角分布的公式进行了拓展[1],为分析QPSK的解调性能奠定了基础,文献[2]在此基础上运用纯几何方法推导了高斯信道下 MPSK统一的条件误码率公式。但以上分析都是基于A/D采样之后,等效基带信号中的相位抖动,这与实际应用中振荡器所产生的相位噪声没有对应关系,无法估计变频器等前端器件的相位噪声对解调性能的影响,限制了 QPSK相干解调的理论分析,文献[3]把相位噪声谱所描述的相位噪声分为了三类,并在DPSK调制方式下分别研究了每一类相位噪声的影响。文献[4]阐述了 VCO相位噪声的特性,分析了时不变和时变两种相位噪声模型。文献[5]研究了OFDM系统中功率放大器的非线性失真和本地振荡器的相位噪声对系统性能的影响。
本文在上述背景下,研究了高斯信道条件不同相位噪声功率谱对QPSK系统的性能影响,利用带有相位噪声的条件误码率公式,分析了不同相位噪声谱所带来的解调损失。
1 相位噪声模型
1.1 单频相位噪声模型
窄带噪声的波形在很短的时间内,我们可以用正弦波来表示[6]。考虑频率fc的单频信号,其功率电平为c,在ifΔ处叠加的单边带相位噪声后可以表示为:


其中oin为单边带相位噪声功率谱密度,iφ是随机相位服从[π,π]- + 上的均匀分布,0in 服从正态分布。fmin和fmax表示所叠加相位噪声的最大频点与最小频点。
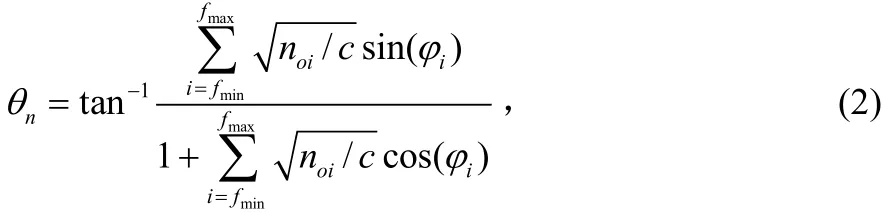

可见对于频率为 fc的单频信号在 Δf处叠加单边带相位噪声后,可以近似等效为在原信号的基础上叠加一个相位抖动,该抖动可以用一个零均值的随机变量来描述。
1.2 混合相位噪声模型
相位噪声功率谱密度通常用dBc/Hz来表示,以 Intelsat Earth Station Standards(IESS-308)标准为例,相位噪声功率谱密度如图1所示。文献[3]把振荡器所产生的相位噪声分为三类,图 1中 A点以左的部分定义为频率抖动噪声(θ1),A点与B点之间定义为白频率噪声(θ2),B点以右的部分定义为白相位噪声(θ3)。
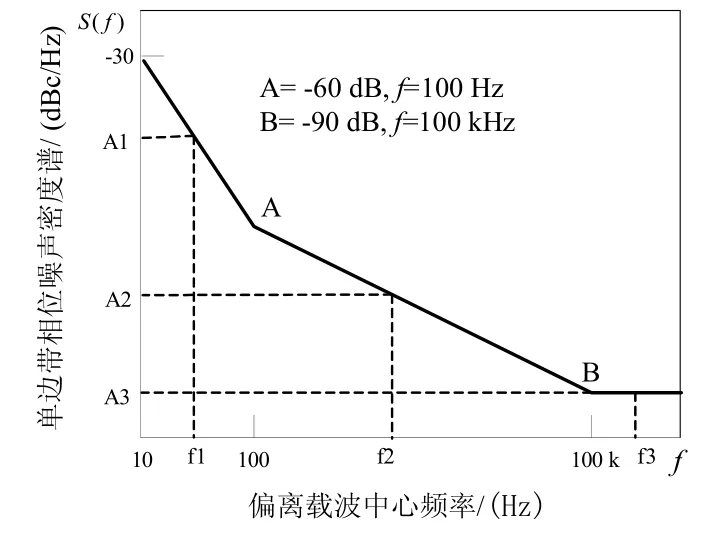
图1 相位噪声功率谱密度
整个相位噪声可以表示为这三种噪声之和,即为:

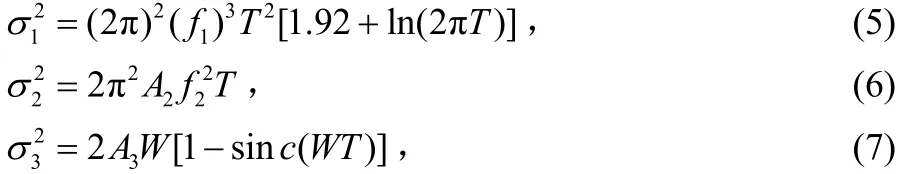
文献[7]指出这三种噪声在一个符号周期内可以看作是零均值高斯随机变量,其方差分别为:其中,T表示符号速率,W表示接收滤波器的带宽。f1是频率抖动噪声的中心频点,A1是频率抖动噪声的功率,f2是白频率噪声的中心频点,A2是白频率噪声的功率,f3是白相位噪声的中心频点,A3是白相位噪声的功率。
2 数值分析
由文献[2]可以推导得到带相位抖动的QPSK误符号率公式为:

其中,sγ为符号的信噪比,nθ表示相位噪声。IESS-308标准定义了适用于卫星链路的相位噪声标准,它主要针对QPSK调制方式下符号速率为9.6kbit/s~2.048 Mbit/s的信号,图2和图3计算了QPSK调制方式,该标准所定义的相位噪声对更低速率信号(R=100 bit/s)和更高速率信号(R=10 Mbit/s)的误比特率影响。
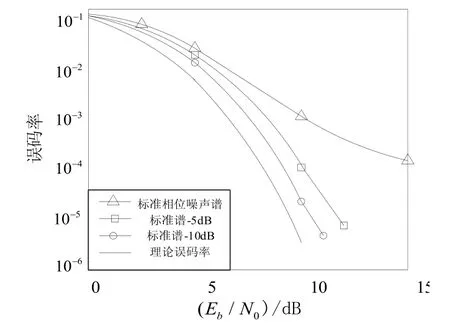
图2 不同噪声谱对低速QPSK的影响
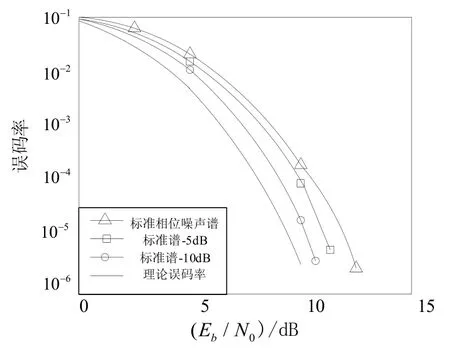
图3 不同噪声谱对高速QPSK的影响
图2、图3中标准相位噪声谱曲线参考IESS-308标准,另外两根曲线分别表示每个频点上叠加的相位噪声功率比标准相位噪声功率小5 dB和10 dB时的误比特率。
与没有相位噪声的理论误码率曲线相比,低速率信号在误码率为10-4时相位噪声带来的解调损失约为6 dB,如果把标准相位噪声谱曲线减小10 dB,则解调损失降低至1 dB左右。但从图3可知,对于高速信号却不能带来同样明显的性能改善。因此在传输R=100 bit/s左右的低速信号的时候,需要参照更加严格的相位噪声谱曲线。
3 结语
本文基于单频相位噪声模型和高斯噪声扰动下两个矢量夹角分布特性,推导了不同相位噪声功率谱密度下QPSK的条件误码率公式,把不同分布的相位噪声与QPSK相干解调统一起来,并通过数值分析的方法研究了不同相位噪声对不同速率信号的影响。利用本文的结论可以从理论上分析不同相位噪声功率谱密度对解调性能的影响,进而可以推广到对其他相位调制方式的理论分析,因此对工程实践具有指导意义。
[1] Pawula R F. Distribution of the Phase Angle Between Two Vectors Perturbed by Gaussian Noise II[J]. IEEE Transaction on Vehicle Technology,2001,50(03):576-583.
[2] Simon M K, Divsalar D. Some New Twists to Problems Involing the Gaussian Probability Integral[J].IEEE Transaction on Communication,1998,46(02):200-210.
[3] Corvaja R, Pupolin S.Effects of Phase Noise Spectral Shape on the Performance of DPSK Systems for Wireless Applications[J].European Transactions on Telecommunications,2002,13(03):203-210
[4] 李长生,王文骐,詹福春.射频应用的压控振荡器相位噪声的研究[J].通信技术,2003(12):26-28.
[5] 刘伟,崔卫国,胡娥梅.非线性失真和相位噪声对DSTBC-OFDM性能的影响[J].通信技术,2007,40(11):110-112.
[6] Robins W P.Phase Noise in Signal Sources[M].London: Peregrinus,Ltd.,1982:12-26.
[7] Iqbal M,Lee J,Kim K.Performance Comparison of Digital Modulation Schemes with Respect to Phase Noise Spectral Shape[C]//Conference on Electrical and Computer Engineering.Halifax,Canadian:IEEE,2000:856-860.

