改进的认知无线电频谱共享博弈模型

黄丽亚，刘臣，王锁萍

（南京邮电大学 电子科学与工程学院，江苏 南京 210003）

1 引言

频谱在无线通信中是稀缺的资源。传统的频谱分配方式静态地分配频谱，频谱利用率很低，很多时候，频谱并没有被完全利用[1]，而近年来对无线服务的需求不断增大，因此频谱资源日益紧张。认知无线电频谱共享技术可以有效地解决频谱资源紧张问题。在认知无线电频谱共享网络中，主用户拥有频谱授权，而次用户没有。具有频谱认知能力的次用户可以利用主用户尚未使用的频谱，主用户通过向次用户出让暂时不用的频谱，能够获得额外收益[2]。

现有的频谱共享方法大致分为两类：一类是针对单个用户进行研究，不考虑用户之间的关系；另一类则对多个用户的合作或竞争关系进行研究[3]。由于实际网络中大多存在多个用户，因此后一类的研究更有实际意义。在多用户竞争的频谱共享方法中，基于博弈论的频谱共享方法是研究的热点。比如Zhao等人提出部分可观察马尔可夫决策模型[4]，Huang等人提出能够限制参与者行为的拍卖竞争模型[5]，Niyato等人提出基于 Cournot博弈的频谱共享模型[6]等。

本文对基于Cournot博弈的频谱共享模型进行了改进。探讨改进模型建立的前提，首先从主用户获得最大收益的角度分析主用户制定最佳单位带宽定价的方法，接着在给定主用户频谱带宽定价的情况下，分析次用户请求带宽大小、次用户相互间的竞争和频谱效率等因素对次用户的收益的影响，分析次用户在静态博弈、动态博弈和相互合作时，选择最佳请求带宽以获得最大收益的方法，最后给出改进模型的性能仿真结果。

2 频谱共享的博弈模型

基于Cournot博弈的频谱共享模型适用于含有单个主用户和多个次用户、频谱资源有限的认知无线电网络中，博弈存在于各个次用户之间，博弈的结果是使每个次用户的收益达到最大。模型给出的主用户单位带宽定价缺乏依据，仅考虑次用户的收益，并且每个次用户的收益仅受到其向主用户请求频谱带宽和频谱效率的影响。

本文对该模型进行改进，将研究的含有多个主用户和多个次用户的认知无线电网络进行简化。首先分析次用户请求的频谱带宽对主用户收益的影响，主用户为获得最大收益该如何选择最佳单位带宽定价，主用户根据预测的次用户可能的请求带宽得出最佳单位带宽定价具有可取性；接着在主用户给定单位带宽定价的前提下，分析次用户收益除受到请求带宽大小和频谱效率的影响外，受到来自其他次用户请求的频谱带宽的影响，分析表明，次用户相互合作比相互竞争能够使各方得到更大收益，说明考虑次用户的收益受到次用户间相互竞争的因素影响是有必要的；最后分析次用户在静态博弈、动态博弈和相互合作时选择最佳请求带宽以获得最大收益的方法，分析表明，次用户在静态博弈、处于稳定区间的动态博弈或相互合作时，都能使各自的请求带宽达到纳什均衡点，从而使收益达到最大。

2.1 无线传输频谱共享系统

认知无线电网络中大多存在多个主用户和多个次用户，主用户拥有频谱的使用权，次用户需要从某一主用户租借频谱带宽。文献[7]指出，多个主用户整合各自的频谱资源，作为一个整体向次级用户提供带宽时，主用户会获得更多的收益，次用户得到的服务质量将会提高，频谱接入费用也会减少。因此，这里将所有主用户视为一个合作的整体，称之为主系统，这样认知无线电网络就简化为由一个主系统和多个次用户组成的系统。

2.2 主系统的最佳带宽定价

主系统的单位带宽定价受所有次用户请求的总带宽影响，主系统需要根据预测的次用户请求的总带宽来制定单位带宽定价，以获得最大收益。

所有次用户的总收益与所获得的总带宽呈非线性关系。虽然次用户得到带宽越多，传输数据得到的收益越多，但是主系统会相应提高单位带宽定价，使得次用户的频谱接入费用提高。次用户的收益一般是关于其获得的带宽的凸函数[8]，这里假设次用户的总收益函数为

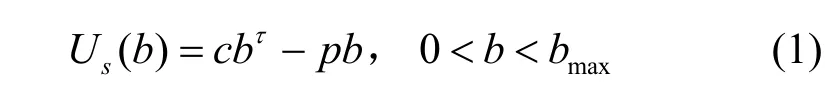
其中，p为主系统的单位带宽定价，b为所有次用户请求的总带宽，c为大于0的常数，τ为取值区间为(0,1)的常数，bmax为所有次用户需要的最大带宽。次用户的收益不会小于0，因此Us(b)总是不小于0。

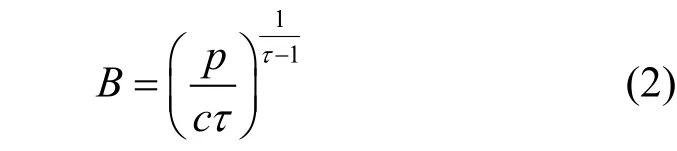
主系统向次用户租让带宽获得收益的同时，得到的服务质量会下降。设服务质量损失为每单位带宽w，次用户请求带宽B，则主系统的收益函数为

对上式进行一阶求导得：

2.3 次用户的静态博弈

主系统确定单位带宽定价后，向次用户提供的总带宽将保持不变。在这种情况下，每个次用户请求带宽的大小要受到其他次用户请求带宽大小的影响，这里用参数ν表示影响的程度[9]。ν取值范围为[0,1]，当ν=0时，次用户不会受其他次用户请求带宽的影响，ν=1时，次用户受其他次用户请求带宽的影响达到最大。

作为数据发送方的次用户i从主系统获得带宽bi后，调整数据传输速率，如果收益为每单位传输速率γi，则次用户i的频谱传输效率为

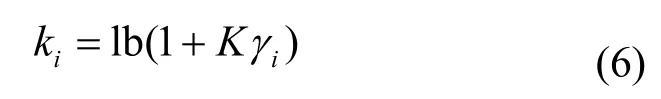
其中，K为由接收方误码率门限决定的常数[10]。

如果主系统采用最佳单位带宽定价P，次用户得到的带宽间的保护带宽忽略不计，则次用户i的收益函数为

具体纳什均衡算法见文献[6]，这里给出结论。从式(7)得到次用户i的最佳请求带宽为

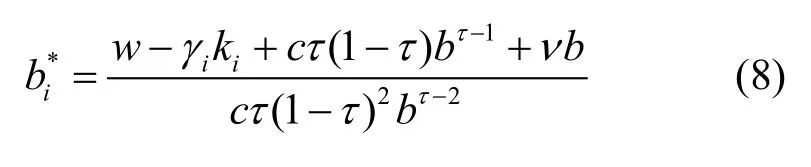
其中，b由下式求得：

2.4 次用户的动态博弈

动态博弈开始时，次用户尝试请求比较少的带宽，然后慢慢增加请求带宽，同时，主系统不断调整单位带宽定价，最终，次用户和主系统的收益都达到博弈时的最大点。

设bi[ t]为次用户i在时刻t请求的带宽，Ui[t]为次用户i在时刻t获得的收益，以下分2种情况讨论。

完全信息动态博弈时，次用户i根据在上一个时刻t其他次用户请求的带宽大小，计算得出时刻t的最佳请求带宽，把它作为在 t+1时刻的请求带宽，即：

不完全信息动态博弈时，次用户i在时刻t试探性地对请求带宽进行略微变化，得到收益与请求带宽的变化关系，在t+1时刻的请求带宽为

其中，参数iα反映次用户i对观察到的收益与请求带宽的变化关系的信任程度[6]。

下面分析不完全信息动态博弈时，次用户请求的带宽能够收敛到稳定状态的稳定区间。由式(11)得：

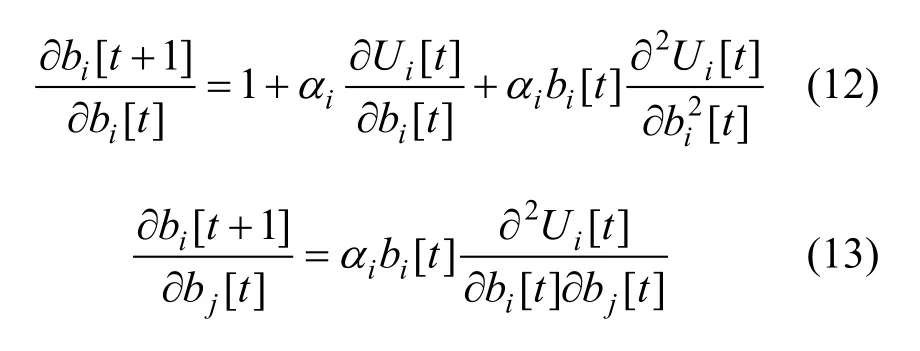
将式(12)、式(13)代入雅各布矩阵，得：

令矩阵J的所有特征值的绝对值小于1，得到iα(i=1,2,…,N)的相互关系，即为不完全信息动态博弈的稳定区间[9]。

2.5 帕累托最优

纳什均衡中，次用户是相互竞争的关系。当次用户相互合作，以总收益最大为目的时，所得到的结果为帕累托最优。分析帕累托最优的算法见文献[9]，这里给出结论。从式(7)得到帕累托最优时次用户i的请求带宽为

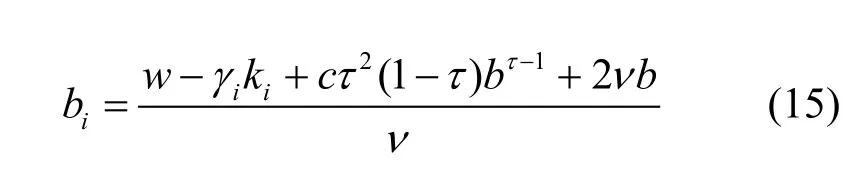
其中，b由下式求得：

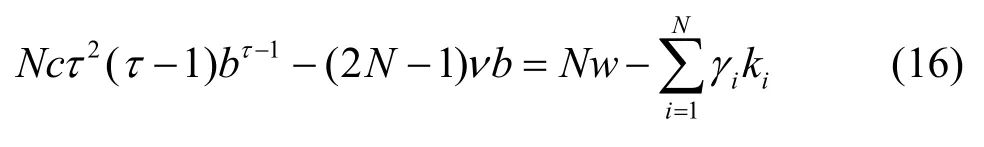
从式(8)和式(15)可以看出，次用户在帕累托最优时的请求带宽比纳什均衡时的请求带宽更大。次用户互相合作可以获得更大收益。

3 仿真结果与分析

本节在 MATLAB环境下，对改进的认知无线电频谱共享模型的静态博弈、动态博弈及其稳定性和帕累托最优进行分析。参数设置：认知无线电系统中有一个主系统和2个次用户，主系统与次用户共享的带宽为20MHz，主系统服务质量损失为每单位带宽 1MHz，2个次用户的误码率门限值为8MHz，每单位传输速率所获得的收益为10dB，参数τ设为0.5，参数ν设为0.4。

3.1 最佳请求带宽和纳什均衡

图1是在不同信道质量条件下，2个次用户最佳请求带宽的关系。从图中可以看出，纳什均衡点的位置受信道质量和参数ν的影响：信道质量提高时，次用户会请求更多的带宽；参数ν增加时，次用户间的影响变大，次用户的最佳请求带宽减少。次用户数量大于2时，以上结论依然成立。当系统存在3个次用户时，每个次用户的最佳请求带宽函数可以表示为一个平面，3个平面的交点即为纳什均衡点。

图1 最佳请求带宽和纳什均衡点

主系统对参数τ的选取直接影响单位带宽定价和次用户请求的总带宽。图2反映不同信道质量条件下，参数τ对主系统收益的影响。从图中可以看出，存在参数τ，使主系统按此制定单位带宽定价时，能获得最大收益。信道质量提高时，次用户会请求更多的带宽，从而主系统可以获得更多的收益。

图2 参数τ不同时主系统的收益

3.2 动态博弈和稳定区间

设动态博弈初始时刻次用户的请求带宽为1MHz，单位传输收益iγ分别为11dB、10dB，次用户请求的带宽随时间的变化如图3所示。从图中可以看出，次用户1和次用户2稳定时刻的请求带宽大约分别为4MHz和3MHz。完全信息动态博弈时，次用户请求的带宽可以很快达到稳定状态；不完全信息动态博弈时，次用户请求带宽的收敛速度依赖于参数iα：iα越大，收敛到稳定状态需要的时间越多，iα超过稳定区间范围时，请求带宽将无法收敛。由于次用户1的单位传输速率收益大，因此次用户1请求的带宽更大。

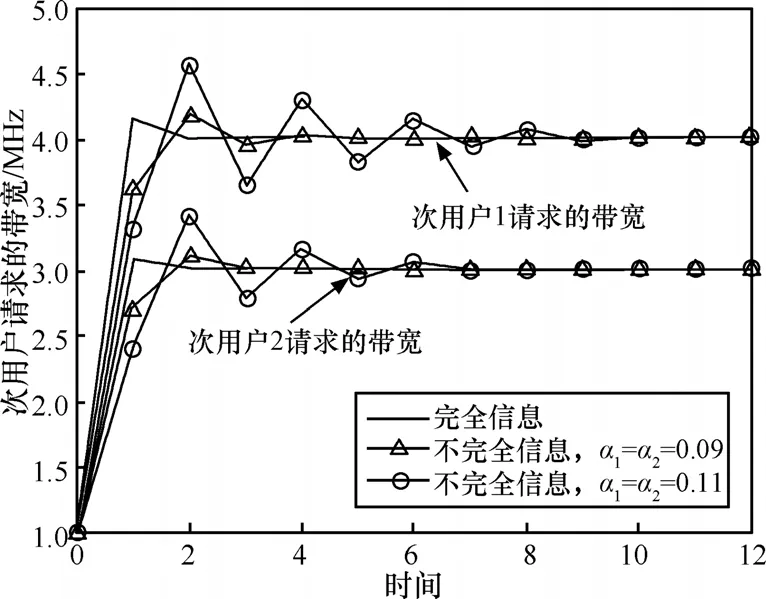
图3 动态平衡收敛到纳什均衡

图4是不同信道质量条件下，不完全信息动态博弈的稳定区间。如果1α和2α取值位于稳定区间内，则次用户在不完全信息动态博弈时，请求的频谱带宽最终能够收敛到稳定状态，否则次用户的请求带宽将一直处于波动状态，无法收敛。信道质量提高，会使稳定区间变小。

3.3 帕累托最优

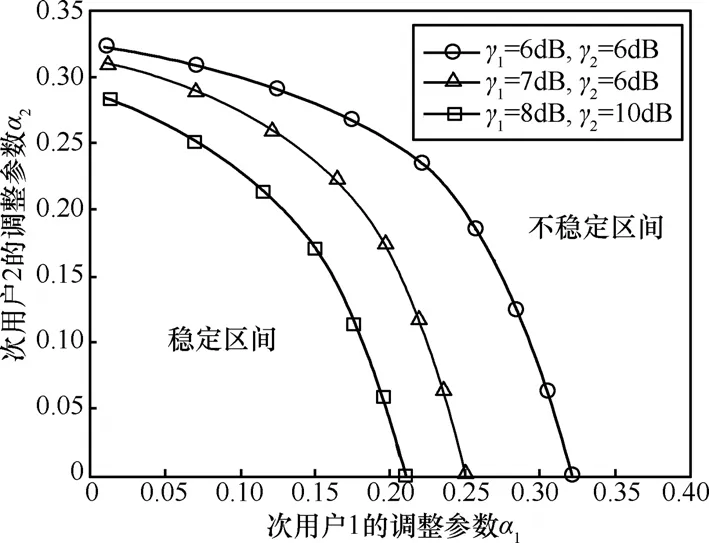
图4 不完全信息动态博弈的稳定区间

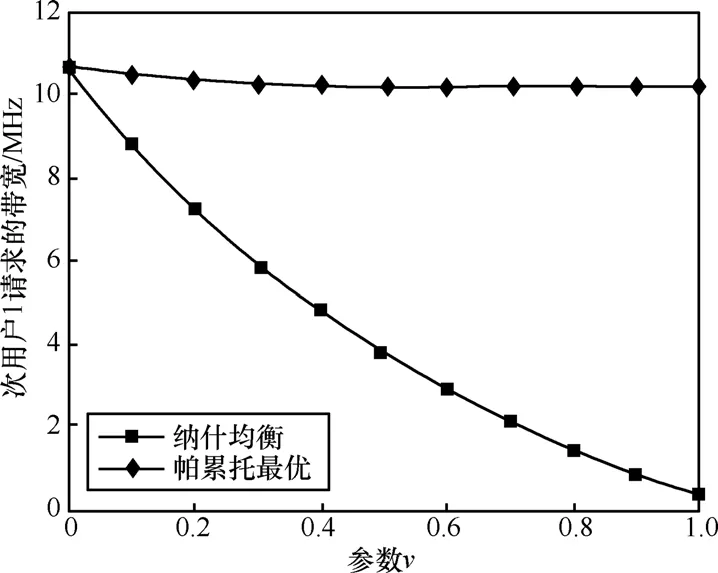
图5 纳什均衡和帕累托最优时的最佳请求带宽

图5反映在纳什均衡和帕累托最优时，次用户1的最佳请求带宽与参数ν的关系。从图中可以看出，帕累托最优时，由于次用户进行合作，相互间几乎没有影响，次用户的请求带宽随参数ν的变化很小；而纳什均衡时，次用户请求的带宽随着参数ν的增大迅速减小；在整个ν区间上，次用户在帕累托最优时请求的带宽比纳什均衡时请求的带宽更大，因此次用户相互合作比相互竞争时能够获得更多的收益。

4 结束语

本文对基于Cournot博弈的频谱共享模型做了改进。改进模型将认知无线电网络中的多个主用户视为一个主系统，综合考虑主系统与次用户间的博弈关系和次用户之间博弈关系，分析主系统该如何选择频谱带宽定价才能获得最大收益，次用户该如何选择请求频谱带宽才能获得最大收益。对该博弈模型的静态博弈、动态博弈及其稳定性和帕累托最优等特性的仿真结果说明改进的博弈模型是合理的。改进的模型适用于频谱资源有限的认知无线电环境中，前提假设是所有主用户相互合作。下一步研究工作将致力于将模型扩展到各个主用户相互竞争，频谱资源丰富的认知无线电网络环境中。

[1] AKYILDIZ I,LI W Y,VURAN M,et al.Next generation/dynamic spectrum access/cognitive radio wireless networks: a survey[J].Computer Networks Journal,2006,9(2): 2127-2159.

[2] BRUCE F.Cognitive Radio Technology [M].New York: Academic Press,2007.

[3] 李琳,曾志民,冯春燕等.认知无线电网络中的非合作频谱分配算法研究[EB/OL].http://www.paper.edu.cn/downloadpaper.php? serial_number=20081-36,2008-12-1.LI L,ZENG Z M,FENG C Y,et al.Research on non-cooperation spectrum allocation algorithm in cognitive radio network[EB/OL].http://www.paper.edu.cn/downloadpaper.php?serial_number=20081-3 6,2008-12-1.

[4] ZHAO Q,TONG L,SWAMI A,et al.Decentralized cognitive MAC for opportunistic spectrum access in ad-hoc networks: a POMDP framework [J].IEEE Journal on Selected Areas in Communications,2007,25(3):589-600.

[5] HUANG J,BERRY R,HONIG M.Auction-based spectrum sharing[J].Mobil Networks and Applications,2006,11(3): 405-408.

[6] NIYATO D,HOSSAIN E.Competitive spectrum sharing in cognitive radio networks: a dynamic game approach[J].IEEE Transaction on Wireless Communications,2008,7(7): 2651-2660.

[7] ALIREZA A,SASWATI S,CHANDRAMANI S,et al.A coalitional game framework for cooperative secondary spectrum access[A].2008 46th Annual Allerton Conference on Communication,Control,and Computing [C].Urbana-Champaign,IL,USA,2008.1154-1160.

[8] 李广久.博弈论基础教程[M].北京: 化学工业出版社,2005.LI G J.The Basic Course of Game Theory[M].Beijing: Chemical Industry Press,2005.

[9] NIYATO D,HOSSAIN E.Competitive pricing for spectrum sharing in cognitive radio networks: dynamic game,inefficiency of nash equilibrium and collision[J].IEEE Journal on Selected Areas in Communications,2008,26(1): 192-202.

[10] GOLDSMITH A J,CHUA S G.Variable rate variable power MQAM for trading channels[J].IEEE Journal on Selected Areas in Communications,1997,45(10): 1218-1230.