陆面潜在蒸散计算模型在甘肃省黄土高原的适用性研究

杨小利,蒲金涌,马鹏里,姚小英

(1.中国气象局兰州干旱气象研究所甘肃省干旱气候变化与减灾重点实验室中国气象局干旱气候变化与减灾重点开放实验室,甘肃兰州730020;2.甘肃省平凉市气象局,甘肃平凉744000;3.甘肃省天水农业气象试验站,甘肃天水741020;4.兰州区域气候中心,甘肃 兰州 730020;5.天水市气象局,甘肃 天水 741000)

陆面潜在蒸散量又称最大可能蒸发量或蒸发力,是指下垫面足够湿润条件下的蒸发量。用来表达气候条件决定各种下垫面蒸发过程的能力。不仅代表某地区的干湿情况,同时亦表示热力条件,是气候学上的一个重要特征。对于土壤含水量乃至水资源的利用评估非常重要[1-4]。由于下垫面状况的复杂性,迄今为止,潜在蒸散的精确测算仍是大气科学中尚未解决的难题之一,在研究中一般都由经验公式计算而得[5-8]。在以往的研究中,曾针对干旱半干旱气候特征,推出了多种潜在蒸散的计算模型。虽然这些模型在解决潜在蒸散的定量估算有一定可信度。但由于模型研究环境的复杂性及针对问题的具体性,在使用这些模型的过程中发现它们都有一定的条件适宜性。在一定地域使用时都要作进一步的订正、评估[9-13]。

自1948年Penman推出潜在蒸散计算模型以来,由于其综合考虑了不同高度和温度下辐射、干燥度及空气动力对蒸散的影响。物理意义明确,使用效果较好,引起了许多学者的兴趣,在这以后几十年的里,衍生出许多订正后的Penman计算模型。其中FAO PPP—17 Penman模型使用最为普遍,我国学者曾使用该方法对区域的蒸散进行过深入的研究,取得了不少成果[14-16]。1998年FAO把经过Monteith订正的Penman公式Penman—Monteith公式推荐作为计算潜在蒸散的标准模型后,该方法的使用更为普遍[17-20]。但在实际研究中,诸如FAO—24 Radiation,Hargvreaves,Priestley—Taylor等计算潜在蒸散的方法,计算过程简便。在缺少某些气象要素测量值时也能使用[21-23]。甘肃省黄土高原为半湿润和半干旱气候的过渡带,陆面潜在蒸散大于降水量,水资源供需矛盾较大。确定适用性较强的潜在蒸散计算模型,可避免因使用模型不同而引起的研究结果的可比性下降,也可为以后的研究提供理论依据。

1 资料及计算模型

1.1 数据资料

西峰国家基准气候站(35°44′N,107°38′E)位于半湿润和半干旱气候的过渡区(年平均气温8.7℃,降水量527 mm,蒸发量1 451 mm),地处黄土高原的东部。气象资料观测始于1937年。本研究资料取自该站1961—2006年的气温、日照、气压、风速、相对湿度、蒸发量的旬平均值。

小型蒸发皿(φ=20 cm)测量的蒸发量,虽然与潜在蒸散有一定差异[1]。但其测量标准统一、方法规范,在表示较大尺度的蒸散趋势中,是唯一具有较长时间序列的实测资料,在研究陆面蒸散时有着不可替代和或缺的作用,是评估各模型的适用性时的主要实测参考量。

1.2 计算模型

1.2.1 FAO98 Penman—Monteith(98) 为 FAO官方1998年推荐作为计算潜在蒸散的惟一标准模型(公式1)。

式中:ET0(98)——潜在蒸散量(mm/d);Rn——净辐射(MJ/m2);G——土壤热通量(MJ/m2);T——日平均气温(℃);ea——饱和水汽压(k Pa);ed——实际水汽压(k Pa);Δ——饱和水汽压—温度的曲线斜率(k Pa/℃);γ——湿度计常数;u2——2 m 高处的风速(m/s)。由于目前气象站普遍无2 m高处风速观测资料,风速用订正公式计算:

式中:h——高度(m);uk——h 高处的风速(m/s)。本研究所用风速资料为气象站按统一标准测得,高度为10.4 m。则风速换算公式为u2=0.738×u10,其中u10为气象站所测风速。

1.2.2 FAO PPP—17 Penman(P—17) 公式(2)是Penman公式的修正式,在国内外应用比较普遍。

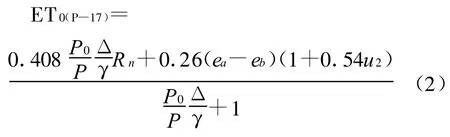
式中:ET0(P—17)——潜在蒸散量(mm/d);P0,P——分别为海平面气压及本站点气压(hPa);Rn,Δ,γ,ea,ed及u2所表示的物理意义及单位与公式(1)相同。

1.2.3 Hargreaves(H) 该模型是Hargreaves和Samani根据在加利福尼亚州8 a间试验用牛毛蒸渗仪数据导出的用气温为作为自变量,同时还引入温度差来反映辐射影响计算潜在蒸散的方法。

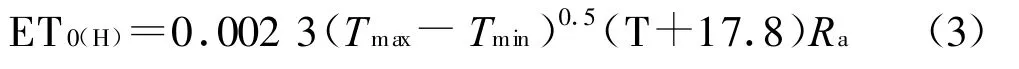
式中:ET0(H)——潜在蒸散(mm/d);Tmax——最高温度(℃);Tmin——最低温度(℃);T——平均温度(℃);Ra——天文辐射(MJ/m2)。

1.2.4 FAO—24Radiation(24R) 该模型源于Makkink公式,主要根据太阳辐射估算蒸散量。

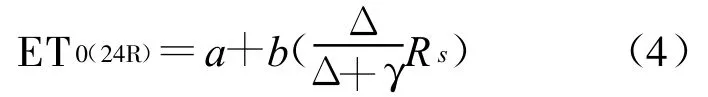
式中:ET0(24R)——潜在蒸散量(mm/d);Δ,γ,u2所代表的物理因子意义及单位如公式(3)。Rs——太阳辐射(MJ/m2);a,b——经验系数,a=-0.3,b=1.066-0.013RHmean+0.045 u2-0.000 2RHmean-0.0 000 315(RHmean)2-0.011u22,其中 RHmean为平均相对湿度(%)。

1.2.5 Priestley—Taylor(P—T) Priestley—Taylor方法是是假设周围环境湿润的前提下,忽略了空气动力学项目而得出的简化方程,应用比较广泛。

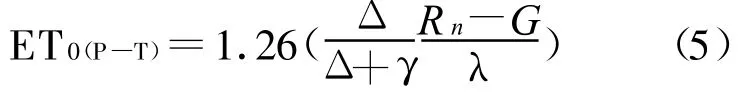
式中:ET0(P—T)——为潜在蒸散量(mm/d);Δ,γ,Rn,G表示的物理量及单位同上述计算式相同;λ——水的汽化潜热,在通常状态(20 ℃)下,λ=2.45 MJ/kg。

2 结果与分析

2.1 模型计算值的年变化

各模型的潜在蒸散计算值的年变化趋势基本与蒸发量相同(图1),最大、最小值出现时间存在不同程度的差异,蒸发量只有Hargreaves的最大值出现在6月,其余各模型都出现在7月;蒸发量的最小值出现在12月,除Hargreaves计算的最小值出现在1月份外,其余各模型均与蒸发量最小值出现时间相同。

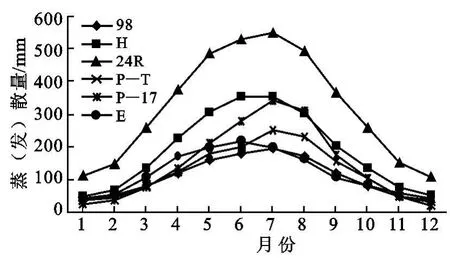
图1 各潜在蒸散模型计算值

根据公式(6)得到各模型的逐月计算值与蒸发量的相对误差。

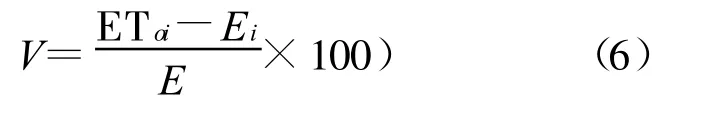
式中:i——月 份;Vi— —i 月的相对 误 差(%);ET0i——模型该月潜在蒸散的计算值(mm);E—该月的蒸发量(mm)。结果表明(表1),98Penman—Monteith,PPP—17及 Priestley—Taylor这 3种模型的潜在蒸散计算值,11—6月小于蒸发量,相对误差为5%～36%。7—10月计算值大于蒸发量,相对误差为1%～9%,模型计算值的偏小幅度大于偏大幅度。7月和10月是相对误差绝对值较小的时段,4月和12月是相对误差绝对值较大的月份。Hargraves及24Radiation模型的计算值均大于蒸发量,相对误差比较大,24Radiation模型相对误差可达238%,Hargreaves模型的最大相对误差也在90%左右,这两种模型的最大误差值都出现在9月。

表1 各种潜在蒸散模型计算值与小型蒸发皿测量值的相对误差 %

2.2 各模型计算值的季节变化及与蒸发量的关系

各计算模型的计算值与同时段的蒸发量(E)、降水量(P)比较分析表明(图2),蒸散模型的计算值的季节分布与蒸发量的四季分布是一致的。夏季是潜在蒸散的最盛季节,小型蒸发所测的蒸发量占全年总量的40%,各种模型的计算值占全年的41%～53%;其次为春季,蒸发量占全年的33%,各种方法的计算值占24%～30%;秋季蒸发量占17%,各种模型的计算值占18%～20%;冬季最少,蒸发量占10%,各种计算模型占5%～10%。秋季降水量大于春季,是一年之中仅次于夏季的第2个降水较多的季节,但秋季的蒸发(散)量却远不及春季。其它季节降水量的分布基本上与蒸发(散)值一致。

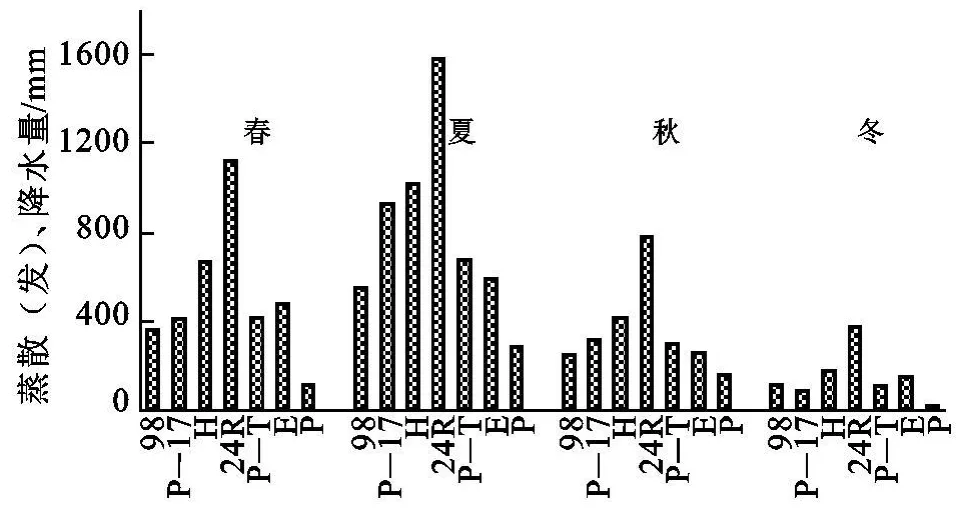
图2 各潜在蒸散计算模型蒸发量(E)、降水量(P)在各季的分布

进一步分析发现,各种蒸散模型的计算量值与蒸发量之间存在比较明显的线性关系(公式7)。用模型的计算值来模拟蒸发量的值,大多数季节都可以取得比较好的效果(表2)。

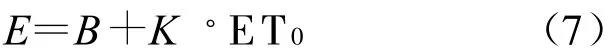
式中:E ——模拟蒸发量(mm);B,K——系数;ET0——模型计算值(mm)。

用研究年份的蒸发量与模型计算值的均方差(公式8)也可作为评估模型对蒸散表达的准确性之一(表 2)。

表2 各种模型不同季节计算值与蒸发量线性模拟系数及均方差值(St)

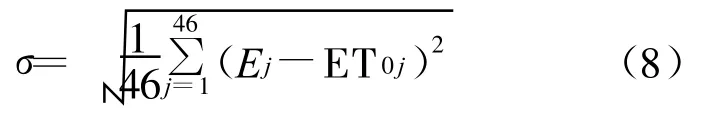
式中:σ——均方差;j——年份;Ej——蒸发量(mm)。各种模型的计算值与蒸发量的相关程度不同。

对98Penman—Monteith模型及PPP—17模型来说,各季节的相关性均很显著,可以通过0.001的信度检验。98Penman—Monteith模型与蒸发量的相关性比PPP—17模型与蒸发量的相关性更为显著。除春季外,其它各季节Penman—Monteith模型与蒸发量的均方差也小于PPP—17模型。Hargreaves模型与蒸发量的相关系数在春、夏两季大于Penman—Monteith模型及PPP—17模型,但在秋、冬两季的相关系数小于上述两个模型,且均方差值均大于上述两个模型。24Radiation模型计算值与蒸发量的相关系数在夏季不能通过0.10信度的水平假设检验,其均方差是所有研究模型最大的,在估算蒸散时应作进一步订正。Priestley—Taylor模型在研究模型中计算值与蒸发量方差均最小,但在夏季其与蒸发量的相关显著性不高,使用时有一定的时间局限。

2.3 各种计算模型的灵敏度分析

灵敏度表示模型中某一参数在其取值发生微小变化时,模型输出结果变化的大小程度〔公式(9)〕[24]。

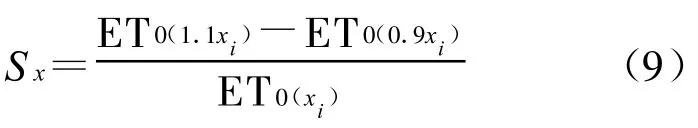
式中:Sx——灵敏度;ET0——模型计算的潜在蒸散量(mm);xi——模型中的某一参数。

根据公式(9)对各个计算方法进行各计算模型的稳定程度分析,得知各种气象因子对不同模型精确度的影响各不相同(表3)。其中对温度变化灵敏程度最高的为PPP-17模型,从仲春至仲秋(4—9月)灵敏度均大于0.10,在年内温度最高的为6—9月,灵敏度大于 0.20;其次为98Penman—Monteith模型和Hargreaves模型,夏季(6—8月)的灵敏度均在0.10以上;Radiation24及Preistly—Taylor模型对温度的变化灵敏度较低,全年均在0.10以下。PPP-17模型对日照变化比较灵敏,4—10月敏感度大于0.10,且年灵敏度为0.16;其余各模型对日照的敏感度均小于0.10。对相对湿度变化比较灵敏的是Preistly—Taylor模型及 PPP-17模型,在 5—10月及 4—9月PPP-17模型及Preistly—Taylor模型的灵敏度均在0.10以上,全年灵敏度也在0.10以上;其余各模型的灵敏度均在0.10以下。对风速变化比较灵敏的模型只有Preistly—Taylor模型,且灵敏度大于0.10的时间在气温较低、风速较大的11月至次年3月。对气压变化较为灵敏的是 Radiation24模型及Preistly—Taylor模型,灵敏度较大的时间是在气压较高的11月至次年3月;而PPP—17模型全年之中只是在12月和1月对气压的灵敏度大于0.10,其余时间均小于0.10。

纵观各模型在不同时段对各气候因子的灵敏程度,温度、日照、湿度因子在4—10月对计算值影响较大,而风速、气压在11月至次年3月影响显著。温度是影响Hargreavs模型的惟一气候因子。98版的Penman—Monteith模型虽然涉及诸多因子,但温度仍是影响模型计算值的最主要因子。而温度、日照及湿度是影响PPP—17模型计算值的主要因子,个别时段气压和风速对其计算值也有影响。温度、日照虽然对Radiation24及Preistly—Taylor模型的计算值影响不大,但风速和气压在个别时间段对其也有影响。

3 结论

(1)所选5种潜在蒸散的计算模型与蒸发量的实测值之间的年际变化趋势基本一致,除Hargreaves模型与蒸发量的最大值同时出现在6月外,其余4个模型的最大值均比蒸发量推后一个月出现;除Hargreaves模型比蒸发量的最小值推后1月,其余各模型的最小值均与蒸发量的出现时间一致。98Penman—Monteith等3种模型的计算值11月至次年6月有8个月的时间大于蒸发量,其余4个月的时间小于蒸发量。Hargreaves及24Radiation模型的计算值始终大于蒸发量,用它们来估算潜在蒸散一般说来是偏大的。

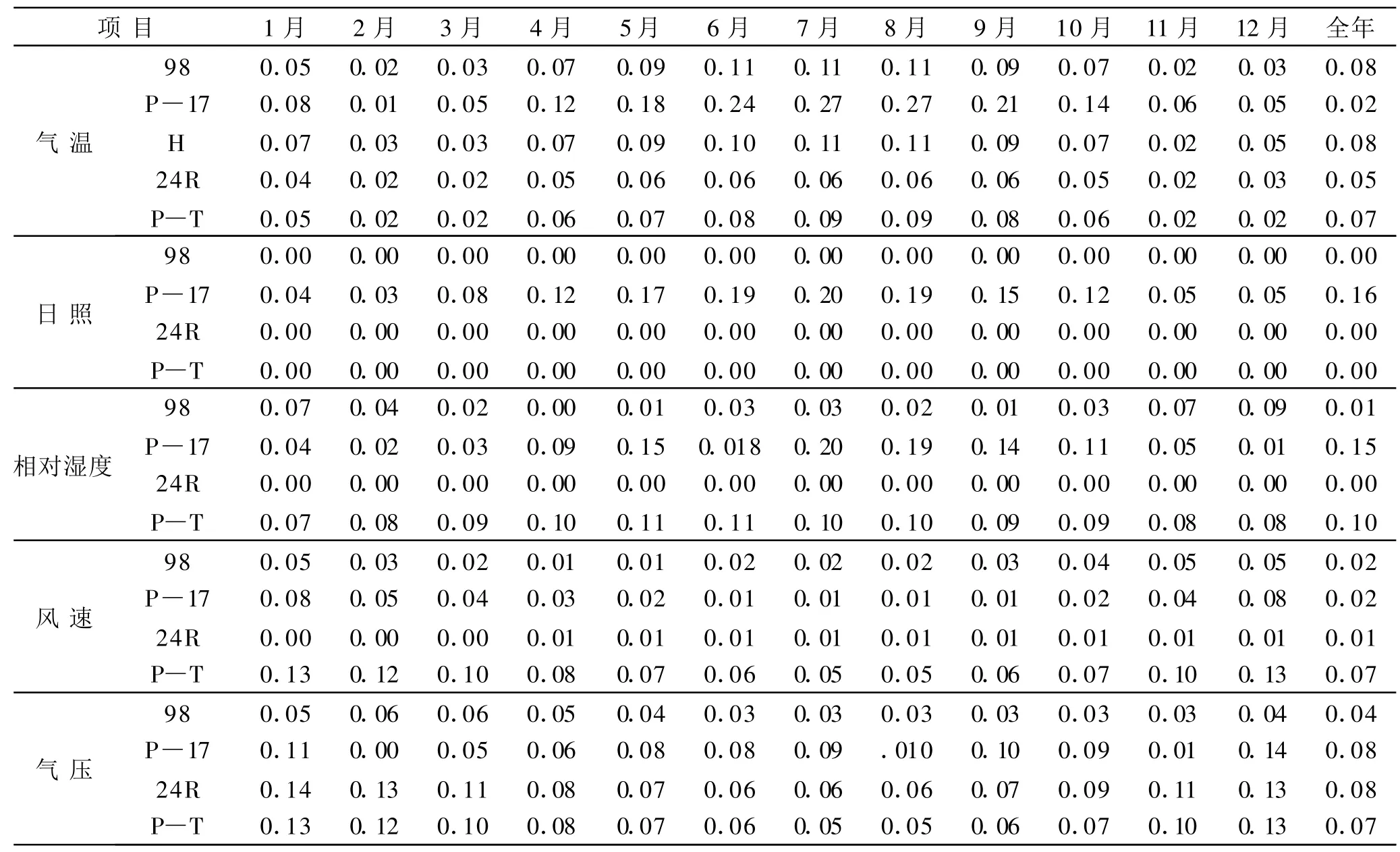
表3 各模型的不同月份的灵敏度

(2)由模型计算值与蒸发量的相关关系及均方差分析可得,在研究模型中,98Penman—Monteith模型4个季节的计算值与蒸发量的相关程度稳定,均方差偏小。是表征潜在蒸散最好的模型;PPP—17在使用中有一定优点,适宜性次之;Hargreaves使用时需要的气候因子较少,且有一定的准确度,尤其在气象资料比较缺乏的地区,有一定的使用价值;Preistly—Taylor模型计算值有一定的参考意义,但夏季的计算值与蒸发量相关显著性较低,在使用时还要做进一步地订正;24Radiation模型的计算值在夏季不能反映蒸发量的多少,且均方差较大,不宜作为计算潜在蒸散的主要模型来考虑。

(3)各种模型对气候因子的灵敏度因时间不同而异。一般来说,温度、日照、相对湿度是影响计算结果的主要因子,其中又以温度的影响最大。温度是明显影响98Penman—Monteith模型计算值的惟一气候因子;气温、日照、相对湿度等 3种气候因子对PPP—17模型均有影响,尤其在6—11月影响较大;98Penman—Monteith和 PPP—17两种模型相比,98Penman—Monteith具有更高的稳定性;Hargreaves模型虽然只有温度一个因子,但其对计算值的影响较大;24Radiation只对气压敏感,其余气候因子对其结果均无明显影响;相对湿度、风速、气压因子只在个别时段对Preistly—Taylor模型的计算值有影响。

[1] 靳亚立,李静,王新,等.近 50年来中国西北干湿状况时空分布[J].地理学报,2004,59(6):847-854.

[2] 刘卉芳,曹文洪,王向东,等.晋西黄土区土壤水分时空分布规律[J].水土保持通报,2008,28(6):105-109.

[3] 郭海英,万信,黄斌,等.气候变化背景下陇东塬区麦田土壤水分变化及生产特征研究[J].水土保持通报,2008,28(3):77-80

[4] 邬春龙,穆兴民,高鹏,等.黄土丘陵区土壤水资源评价与分析[J].水土保持通报,2007,27(6):189-193.

[5] 马耀明,王介民.非均匀陆面上蒸发(散)研究概况[J].高原气象,1997,16(4):446-452.

[6] 毛飞,张光智,徐祥德.参考作物蒸散量的多种计算方法及其结果的比较[J].应用气象学报,2000,11(S):128-136.

[7] 许迪,刘钰.测定和估算田间植物腾发量方法研究综述[J].灌溉排水,1997,16(4):54-59.

[8] 武夏宁,胡铁松,王贵秀,等.区域蒸散发估算测定方法综述[J].农业工程学报,2006,22(10):257-261.

[9] 刘钰,Pereira L S.对FAO推荐的作物系数计算方法的验证[J].农业工程学报,2000,16(5):26-30.

[10] 刘钰,蔡根林.参考腾发量的新定义及计算方法对比[J].水利学报,1997,28(6):27-33.

[11] 刘晓英,林尔达,刘培军.Priestley—Taylor与 Penman法计算参照作物腾发量的结果比较[J].农业工程学报,2003,19(1):32-36.

[12] Chiew F H S,Kamamaladasa N N,Malano H M,et al.Penman—Monteinth,FAO-24 reference crop evapotranspiration and class-A pan data in Australia[J].Agr.Water Mgmt.,1995,28:9-21.

[13] Hobbins M T,Ramirez J A,Brown T C.The complementary relationship in regional evapotranspiration:the CRAE model and the Advection-aridity approach[J].Proc.Annual A.G.U.Hydrology Days,1999,37(5):199-212.

[14] 高国栋,陆渝蓉,李怀瑾.我国最大可能蒸发量的计算和分布[J].地理学报,1978,33(2):102-107.

[15] 钱纪良,林之光.关于中国干湿气候区划的初步研究[J].地理研究,1965,31(1):1-12.

[16] 李林,张国胜.黄河上游流域蒸散量及其影响因子研究[J].地球科学进展,2000,15(3):256-259.

[17] R G Allen,L S Pereira,Raes D,et al.Crop evapotranspiration buidelines for computing crop water requirements-FAO irrigation and drainage paper 56[M].Rome:FAO-Food and Agriculture Organization,1998.

[18] 郭晓寅,程国栋.遥感技术应用于地表面蒸散发的研究进展[J].地球科学进展,2004,19(1):107-114.

[19] 杨小利,杨兴国,马鹏里,等.PDSI在甘肃中东部地区的修正和应用[J].地球科学进展,2005,20(9):1022-1028.

[20] 李晓军,李取生.东北地区参考作物蒸散确定方法研究[J].地理科学,2004,24(2):212-216.

[21] 刘晓英,林尔达,刘培军.干旱条件下Priestley-Taylor方法应用探讨[J].水利学报,2003,(9):31-39.

[22] 史晓南,王全九,王新,等.参考作物腾发量计算方法在新疆地区的适用性研究[J].农业工程学报,2006,22(6):19-23.

[23] 张国威,周聿超.新疆内陆干旱区蒸发的计算与分析[J].水科学进展,1992,3(3):26-232.

[24] 彭世彰,徐俊增.参考作物蒸发蒸腾量计算方法的应用比较[J].灌溉排水学报,2004,23(6):5-9.

[25] 刘绍民,孙中平,李小文,等.蒸散量测定与估算方法的对比研究[J].自然资源学报,2003,18(2):161-167.