基于ANSYS的公路复杂桥梁车桥耦合动力分析方法
施 颖,宋一凡,孙 慧,周新平
(1. 长安大学公路学院,西安 710064;2. 浙江工业大学建筑工程学院,杭州 310014;3. 天津大学管理学院,天津 300072;4. 中交第一公路勘察设计研究院有限公司,西安 710075)
车辆过桥时将引起桥梁结构的振动,而桥梁的振动又反过来影响车辆的振动,这种相互作用、相互影响的问题是车桥耦合振动问题.其研究自 1825年人类有了第一条铁路就开始了[1-2].在 20世纪 60年代以前,对于车桥耦合振动的研究主要集中在简单移动荷载作用下的解析方法.计算机的出现和有限元法在工程上的应用,使得建立复杂的车桥耦合振动分析模型成为可能.
近年来,由于高等级公路修建,桥跨越来越大、墩高越来越高,车速也大幅提高,交通流量显著增长,重载车辆大量涌现,这些原因引起的车桥耦合振动已经不可忽视,因此车桥动力分析问题也越来越吸引桥梁界人士更多的关注和重视.在过去的几十年中,在设计桥梁时大多仅做静力分析,动力分析往往仅涉及到结构的振动特性及地震响应、风效应方面,至于车对桥的作用仅采用冲击力规范公式予以考虑,很少涉及到车与桥相互作用和影响的车桥耦合动力分析领域.虽然学者们对车桥耦合振动的研究已有近百年的历史,但迄今为止仍没有达到十分完善和成熟的水平,既有研究成果仍存在许多尚未解决的技术难题,因此非常有必要开展复杂桥梁车桥耦合振动及其影响分析的研究.
目前研究车桥耦合振动系统常用的分析方法有以下两种:一种是用直接积分法求解耦合车桥系统运动方程,可给出没有迭代过程的时程结果,但仅限于简单桥梁;另外一种是把车桥耦合问题处理成两种不同的运动方程系统,一个用于桥梁振动分析,另一个用于车辆振动分析,用轮与桥面(轨面)竖向位移协调来考虑车与桥的接触,适合于分析复杂结构体系桥梁、多自由度车辆模型的车桥耦合振动分析.国内许多学者均致力于后者的研究[3-7],并应用有限元的方法,但也要编制专用复杂程序计算.
随着有限元技术的广泛应用和大型结构分析软件的大量涌现,为了方便实用、避免编制复杂专用程序,研究一种基于既有有限元分析软件的数值分析方法,以实现对复杂桥梁结构(如弯桥等)车桥耦合振动及其影响的分析,具有理论意义和应用前景.笔者采用本文方法首先通过简支梁桥算例与参考文献比较,然后对曲线连续梁桥在各影响因素(如不同车速、桥面不平度及是否考虑动离心力等)下进行了动力系数求解,并与规范值对比,两者均有较好的吻合度,从而验证了此分析方法的可行性.
1 车桥耦合振动分析原理与方法
目前车桥系统动力相互作用分析的经典方法有移动力作用模型、移动质量作用模型、移动车轮+簧上质量作用模型等[8],这几种方法都是在梁强迫振动微分方程的基础上,利用振型叠加法和振型的正交特性推导出了桥梁的车桥系统动力平衡方程组,并编制专用复杂程序求解.
由文献[9]知,车辆模型的差异对计算结果的影响很小,故本文只建立了1/2车与桥相互作用的力学分析模型,并把车和桥视作两个分离体系,应用广义虚功原理[10]和有限元法推导了两者的振动方程组,通过位移协调等方程来实现求解.
1.1 车辆模型及振动方程推导[11]
图1所示为简化为两系的弹簧-阻尼-质量系统的4自由度车辆模型,图中:M为车体质量,两个自由度分别为竖向位移 Z和绕横向轴的旋转自由度α;m为构架质量与轮对质量之和,每个块质量被赋予了一个竖向位移自由度(z1,z2);sk为二系垂向刚度;sc为二系垂向阻尼;tk为一系垂向刚度;tc为一系垂向阻尼;支承车体点的竖向位移自由度分别记为1z′和2z′.

图1 1/2车辆模型作用下的简支梁桥Fig.1 Simply-supported girder bridge subjected to,1/2 vehicle model
按图1所示坐标定义,则待求未知位移向量为

车辆模型中的力分别为:重力(Mg、im g,i=1,2)、惯性力悬置力Fsi和轮胎力 Fti,
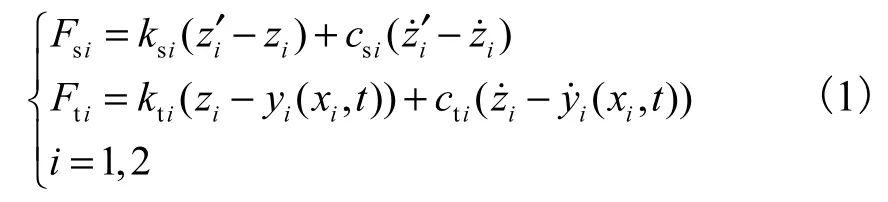
由几何关系可得

由广义虚功原理得
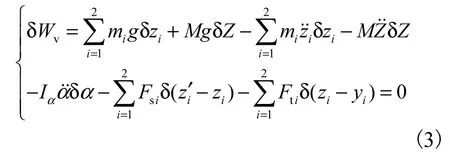
将式(1)、(2)代入式(3),展开得到
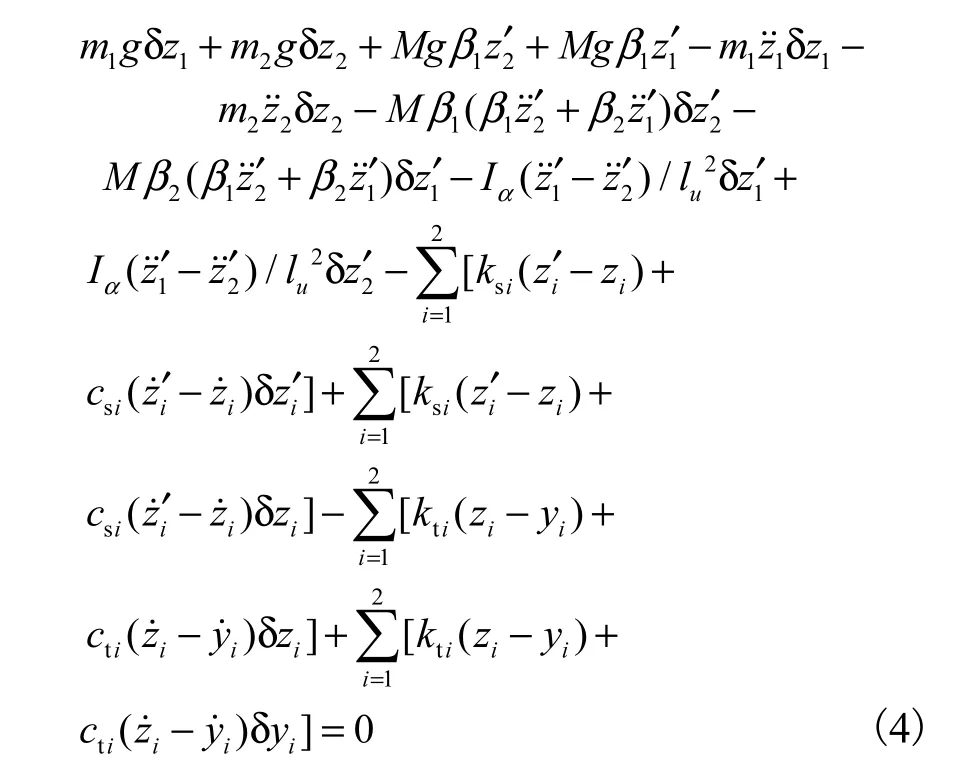
式中:bvF 为车辆的轮胎与桥面接触点处的瞬时耦合荷载向量;vG为重力荷载向量;vM 为车辆的质量矩阵;vC为车辆的阻尼矩阵;vK为车辆的刚度矩阵.
1.2 桥跨结构动力平衡方程
目前应用较多的大跨度桥梁主梁的计算模型主要有 3种:鱼骨式、双梁式和三梁式.无论哪种模型,桥梁结构最终的振动方程[11]可写为

式中:M为桥梁的质量矩阵;C为桥梁的阻尼矩阵;K为桥梁的刚度矩阵;˙˙X、˙X、X分别为桥梁节点的加速度、速度和位移向量;F为作用在桥梁节点上的力列向量.
1.3 位移联系方程及车桥相互作用[11]
1.3.1 位移联系方程
假设车轮在运行的过程中始终与桥面密贴不脱离,则使得车桥成为一个系统,轮对的位移可通过梁的相应位移表示,其方程成为联系方程,即

式中:zi为车辆第 i个轮胎由静平衡位置起算的竖向位移;dri为行车路线的外形(dx)在作用点处的坐标(包括桥梁预拱度和桥面不平整等);yi为桥梁在第 i个轮胎作用下的瞬时变位;ui为车辆各轴悬挂弹簧的相对位移.
1.3.2 车桥相互作用
将车辆和桥梁视作两个分离体系,二者之间耦合作用通过轮胎与桥面间的相互作用联系起来.轮胎与桥梁间的相互作用力可描述为[12-13]

式中:ki为第i个轮胎的刚度;ci为第i个轮胎的阻尼系数;ui、 u˙i为第i个轮胎与桥梁的竖向联系位移和相对速度.
1.4 车桥耦合振动有限元数值计算方法
基于 ANSYS车桥耦合振动数值分析的具体方法、步骤及分析流程如图2所示.
(1)基于 Matlab平台,采用 Wilson-θ法编程求解,得到车辆振动时间和速度、时间和位移等响应时程序列.
(2)利用既有大型通用结构的分析软件 ANSYS建立计算模型,求得桥梁振型与频率.
(3)根据第(2)步计算得到的桥梁基频,结合划分单元数,综合考虑车速等因素,选取合适的时间积分步长(积分步长一般可取为 Δ t ≤ T /15).
(4)将车辆与桥梁接触点联系位移及相互作用力,输入由 ANSYS建立的车桥振动相互作用有限元模型中,利用其瞬态动力学分析功能实现数值求解.
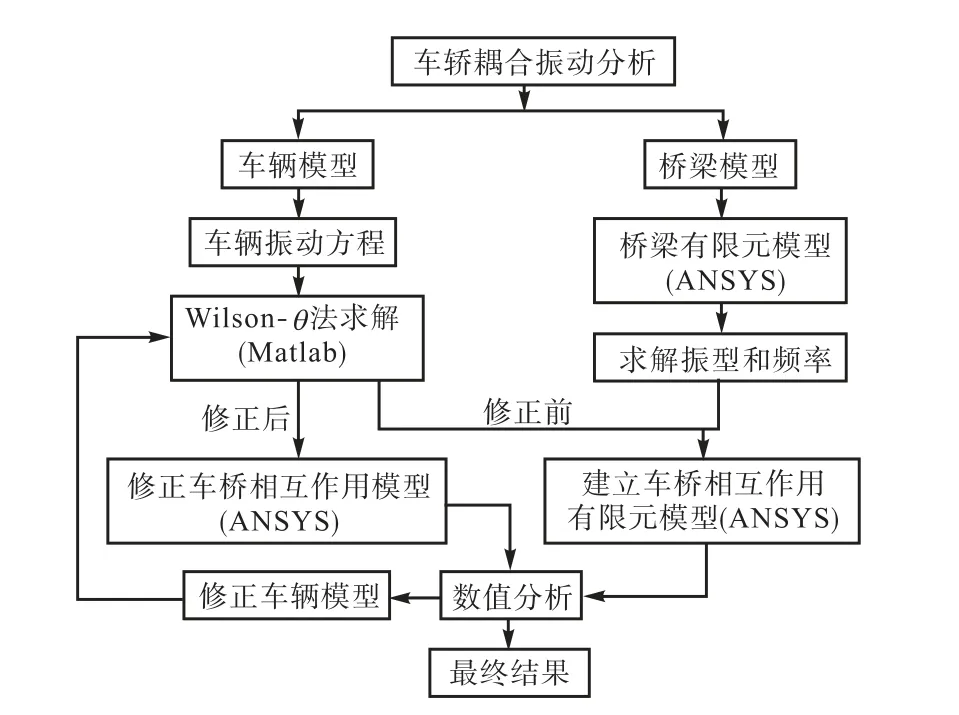
图2 车桥耦合振动数值分析流程Fig.2 Flow chart of numerical analysis of, vehicle-bridge coupled vibration
(5)用第(4)步求解得出的位移、速度重复第(1)步进行修正车辆模型,再重复第(4)、第(5)步,如此循环直到前后两次响应曲线接近重合,即得最终解.
1.5 车桥耦合振动有限元数值计算方法比较
简支梁桥动力分析模型如图 1所示.车辆的技术参数按表 1[3]取值,桥梁参数如下:跨径为 32,m,单位长度质量为5.41×103,,kg/m,抗弯刚度为3.5×1010N·m2.按本文方法分别求解车速为 120,km/h和160,km/h 时,以车辆响应曲线零点、0.5、1.0、1.5、2.0周期为计算起点的简支梁桥跨中位移响应曲线.计算结果与文献[3]按 Ruge-Kutta法计算结果比较列于图3和图4,结果表明,本文以车辆响应曲线2周期(见图 5和图 6)为计算起点得到的结果与文献[3]计算结果基本吻合,说明该方法是可行的.

表1 车辆技术参数Tab.1 Technical parameters of vehicle

图3 简支梁跨中位移响应曲线比较(120,km/h)Fig.3 Comparison of response curves of vertical displacement at middle strip for simplysupported beam(120,km/h)
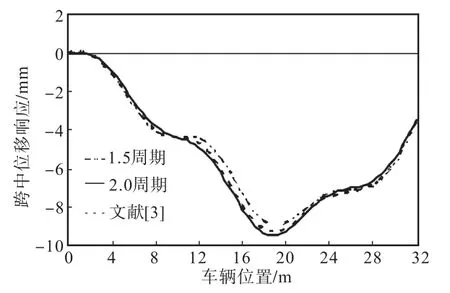
图4 简支梁跨中位移响应曲线比较(160,km/h)Fig.4 Comparison of response curves of vertical,displacement at middle strip for simply-,supported beam(160,km/h)

图5 车辆位移响应曲线Fig.5 Response curve of vehicle displacement

图6 车辆速度响应曲线Fig.6 Response curve of vehicle velocity
2 曲线连续梁桥车桥耦合振动数值分析
2.1 动力分析模型与技术参数
图7、图 8所示为 1/2车模作用下的连续弯梁桥动力分析模型和横断面图.车辆技术参数按表 1取值,桥梁参数如下:跨径为3×25,m的连续梁,曲率半径为 200,m,单位长度质量为 9.3×103,kg/m,竖向抗弯刚度为 3.21×1010,N·m2,横向抗弯刚度为 5.01×1011,N·m2,抗扭刚度为 7.19×1010,N·m2.
2.2 不同车速对车桥耦合振动影响分析

图7 1/2车辆模型作用下的连续弯梁桥Fig.7 Curved beam bridge subjected to 1/2 vehicle model
按本文方法分别求解车速为 40~120,km/h时桥梁振动响应.曲线连续梁中跨跨中及边跨跨中竖向位移响应曲线和动力系数对比结果分别如图 9~图12所示.
由图9~图12分析可知:
(1)无论车辆的速度是多少,桥梁的最大动位移都发生在跨中附近;
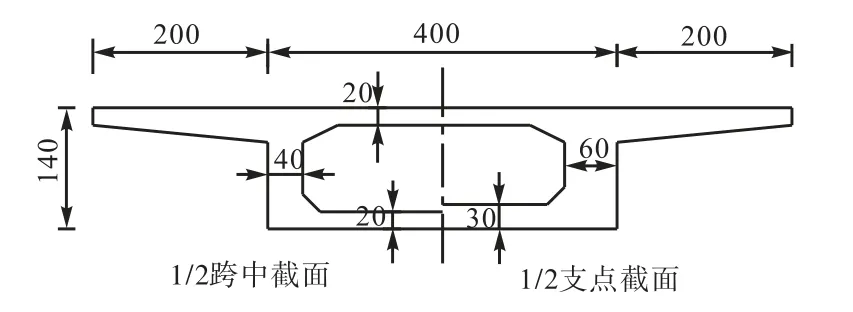
图8 连续弯梁桥截面示意(单位:cm)Fig.8 Cross-section sketch of curved beam bridge(unit:cm)

图9 曲线梁桥中跨跨中竖向位移响应曲线比较Fig.9 Comparison of response curves of mid-span vertical ,displacement at middle strip of curved beam bridge
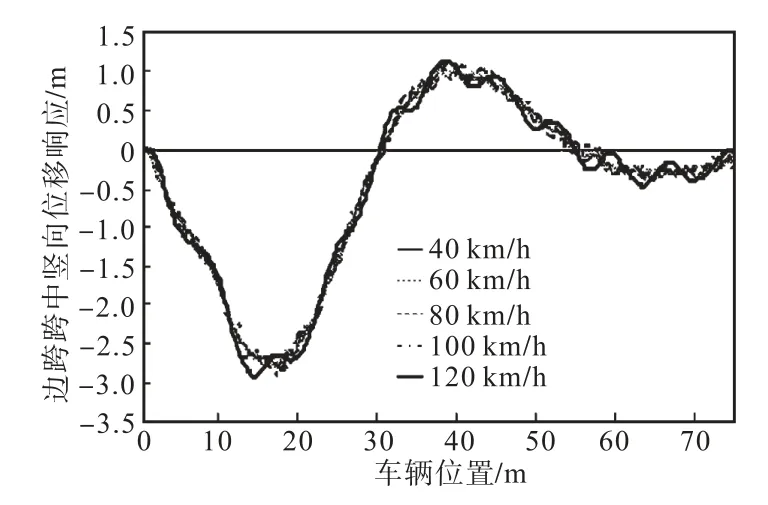
图10 曲线梁桥边跨跨中竖向位移响应曲线比较Fig.10 Comparison of response curves of side-span vertical displacement at middle strip of ,curved beam bridge
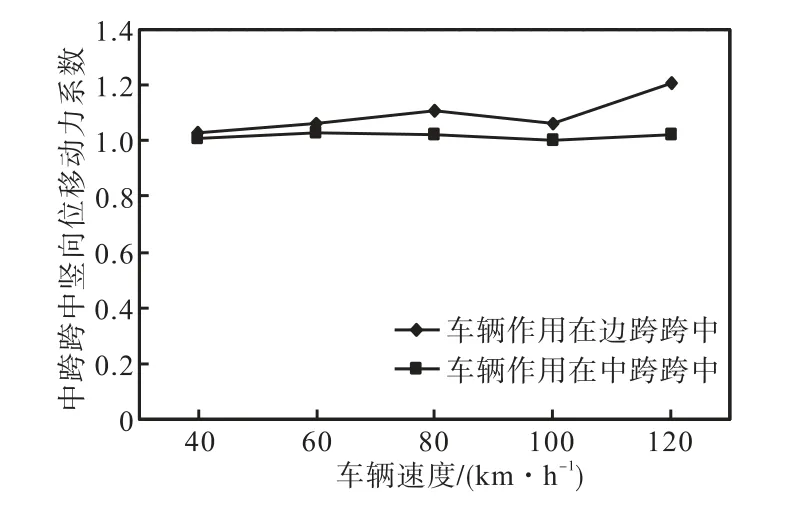
图11 中跨跨中竖向位移动力系数与车速的关系Fig.11 Relationship between power coefficient of mid-span vertical displacement at middle strip and vehicle speed

图12 边跨跨中竖向位移动力系数与车速的关系Fig.12 Relationship between power coefficient of side-span vertical displacement at middle,strip and vehicle speed
(2)随着车速的增加,振动响应波动的幅值越来越大,频率越来越低,周期变长;
(3)对各种车速,当车辆经过在边跨跨中位置的前后时刻,中跨跨中的动力系数达到最大;而当车辆经过在中跨跨中位置的前后时刻,边跨跨中的动力系数达到最大;
(4)中跨和边跨跨中竖向位移最大动力系数先随着车辆速度的增加而增大,在车速 80,km/h时出现一个转折点,取得极值出现了共振现象.
2.3 桥面不平整度对车桥耦合振动影响分析
路面不平整度是指路表面相对于基准平面的偏离程度.大量的试验测量结果表明,路面不平整是具有零均值、各态历经的平稳 Gauss随机过程.在实际中,通常用功率谱来描述路面的统计特性,且路面不平整度的功率谱密度可拟合为[14]

式中:n为空间频率,m-1;n0为参考空间频率,n0=0.1,m-1;Gx( n0)为路面不平度系数;Gx( n)为位移功率谱密度;w为频率指数,取w=2.
根据 GB/T 7031—1986,据统计我国高等级公路基本属于 A、B、C 3个等级[15],桥面大多相当于公路C级路面.图 13是根据文献[14]的数值模拟方法得到的公路A、B和C级路面的不平整度曲线.计入桥面不平整度的桥梁中跨跨中和边跨跨中的动力系数计算结果汇总于表2.
由图 11、图 12与表 2的对比分析可知:计入桥面不平整度后,桥梁的振动响应波动的幅值明显增大,频率变低、周期变长,且桥梁的最大动力系数由原来的 1.24增大到 1.58,故桥面不平整度对桥梁的车桥耦合振动影响很大,这正好与文献[7]认为桥面平整度是影响桥梁车激振动的主要因素之一相吻合,分析时应予以考虑.

表2 动力系数计算结果汇总Tab.2 Summary of dynamic coefficient calculation

图13 A、B和C级桥面的不平整度曲线Fig.13 Roughness curves of grade A,B and C pavement
2.4 车辆离心力对车桥耦合振动的影响分析
图14和图 15是按本文方法分别求得车速60,km/h时不计车辆动离心力和计入车辆动离心力的桥梁振动响应时程曲线,其中离心力的计算按 JTG D60—2004第 4.3.3.1条规定进行,并移至桥梁截面的中心处.限于篇幅,本文只列出中跨跨中竖向位移和扭转角时程曲线两者对比.
由图14和图15对比分析可知:离心力对桥梁竖向动态响应影响不大(图中两曲线基本重合),但使桥梁扭转角动态响应加剧.

图14 中跨跨中竖向位移时程曲线比较Fig.14 Comparison of time-history curves of mid-spanv ertical displacement at middle strip

图15 中跨跨中扭转角时程曲线比较Fig.15 Comparison of time-history curves of mid-span twist angel at middle strip
3 结 语
按JTG D60—2004给定的连续梁基频估算公式得出本算例计算冲击力引起的正弯矩效应和剪力效应时的基频 f=6.441,Hz,由此计算的冲击系数为0.313,换算为动力系数为 1.313,对中跨来说仅大5.6%,基本吻合,但对边跨来说减幅高达 20.3%,存在着不安全的隐患,应引起重视.
通过简支梁算例计算结果与参考文献结果的比较分析可知,以车辆响应曲线2.0周期为计算起点并经两次修正后,数值分析得到的桥梁响应曲线具有较好的精度;通过连续梁计算结果与规范比较也有较好的吻合度,这充分验证了本文利用既有有限元程序实现车桥耦合振动响应数值分析方法的可行性,从而为研究复杂桥梁(如连续弯桥、高墩连续刚构、拱桥、斜拉桥等)车桥耦合提供了一种简便而可靠的数值分析方法.
[1] IM Biggs. Introduction to Structural Dynamic[M]. New York:McGraw-Hill Book Co,Inc,1964.
[2] Fryba L. Vibration of Solids and Structures Under Moving Loads [M]. The Netherlands:Noordhoff International Publishing Groningen,1972.
[3] 沈火明,肖新标. 求解车桥耦合振动问题的一种数值方法[J]. 西南交通大学学报,2003,38(6):658-662.Shen Huoming,Xiao Xinbiao. Numerical method for ve-hicle-bridge couple vibrations[J]. Journal of Southwest Jiaotong University,2003,38(6):658-662(in Chinese).
[4] 王解军,张 伟. 汽车荷载作用下梁桥的动力冲击效应研究[J]. 振动与冲击,2007,26(6):125-128.Wang Xiejun,Zhang Wei. Power effect of impact of beam bridge under vehicular loads[J]. Journal of Vibration and Shock,2007,26(6):125-128(in Chinese).
[5] 刘 华,叶见署,张 涛. 连续梁在行驶车辆作用下的动态反应[J]. 交通运输工程学报,2006,6(2):26-29,34.Liu Hua,Ye Jianshu,Zhang Tao. Dynamic response of continuous girder bridge under moving vehicular loads[J]. Journal of Traffic and Transportation Engineering,2006,6(2):26-29,34(in Chinese).
[6] 单得山,李 乔. 铁路曲线连续梁桥车桥耦合振动分析[J]. 中国铁道科学,2004,25(5):20-25.Shan Deshan,Li Qiao. Analysis of vehicle-bridge coupling vibration on railway curve continuous beam bridge[J]. China Railway Science,2004,25(5):20-25(in Chinese).
[7] 王潮海,王宗林. 车-桥耦合振动分析的模态综合方法[J]. 公路交通科技,2006,23(12):76-80,90.Wang Chaohai,Wang Zonglin. Dynamic analysis on coupled vehicle-bridge system by modal synthesis method[J]. Journal of Highway and Transportation Research and Development,2006,23(12):76-80,90(in Chinese).
[8] 宋一凡. 公路桥梁动力学[M]. 北京:人民交通出版社,2000.Song Yifan. Dynamics of Highway Bridge[M]. Beijing:The People’s Communications Publishing House ,2000(in Chinese).
[9] 申永刚. 大跨度 CFRP拉索斜拉桥的模态阻尼特性研究[D]. 杭州:浙江大学建筑工程学院,2008.Shen Yonggang. Modal Damping of Long-Span Cable-Staved Bridges with CFRP Cables[D]. Hangzhou:College of Architectural Engineering,Zhejiang University,2008(in Chinese).
[10] 曾庆元.弹性系统动力学总势能不变值原理[J]. 华中理工大学学报,2000,28(1):1-3.Zeng Qingyuan.The principle of total potential energy with stationary value in elastic system dynamics[J].Journal of Huazhong University of Science &Technology,2000,28(1):1-3(in Chinese).
[11] 王亚昆. 大跨度自锚式悬索桥车桥耦合振动数值分析[D]. 西安:长安大学公路学院,2008.Wang Yakun. Vehicle-Bridge Coupled Dynamical Numerical Analysis for Long Span Self-Anchored Suspension Bridge[D]. Xi′an:School of Highway,Chang’an University,2008(in Chinese).
[12] Henchi K,Fafard M,Talbot M,et al. An efficient algorithm for dynamic analysis of bridge under moving vehicles using a coupled modal and physical components approach[J]. Journal of Sound and Vibration,1998,212(4):663-683.
[13] Huang D Z. Dynamic analysis of steel curved box girder bridges [J]. Journal of Bridge Engineering,2001,6(6):506-513.
[14] 宋一凡,陈榕峰. 基于路面不平整度的车辆振动响应方法[J]. 交通运输工程学报,2007,7(4):39-43.Song Yifan,Chen Rongfeng. Analysis method of vehicle vibration response caused by pavement roughness[J].Journal of Traffic and Transportation Engineering,2007,7(4):39-43(in Chinese).
[15] 余志生. 汽车理论[M]. 5版.北京:机械工业出版社,2009.Yu Zhisheng. Automobile Theory[M].5th ed. Beijing:China Machine Press,2009(in Chinese).

