路面温度场的数值解及几个关键问题探讨

谈至明,邹晓翎,刘伯莹

(1.同济大学 道路与交通工程教育部重点实验室,上海 201804;2.中交桥梁技术有限公司,北京 100029)

路面结构温度场的影响因素众多,在以往的研究中常采用一些简化或近似处理,例如,层状的路面结构等效简化为均质半无限体,路面与天空的相互辐射与温度关系线性化,天空有效温度用气温代替等等[1-3].但是,对这些简化或近似处理方法带来的偏差的研究欠深入,由此获得的路面温度场分析结果精度难以估计.因此,弄清这些简化或近似处理方法所带来的偏差,对于深化路面温度场的研究和提高其分析精度具有重要意义.

1 路面的热传导问题及差分解

对于厚度方向远比平面尺寸小很多的路面结构来说,其温度场可视为厚度方向一维热传导问题.当路面各结构层之间接触良好且无热阻情况下,路面温度场Ti(x,t)的偏微分方程可表示为

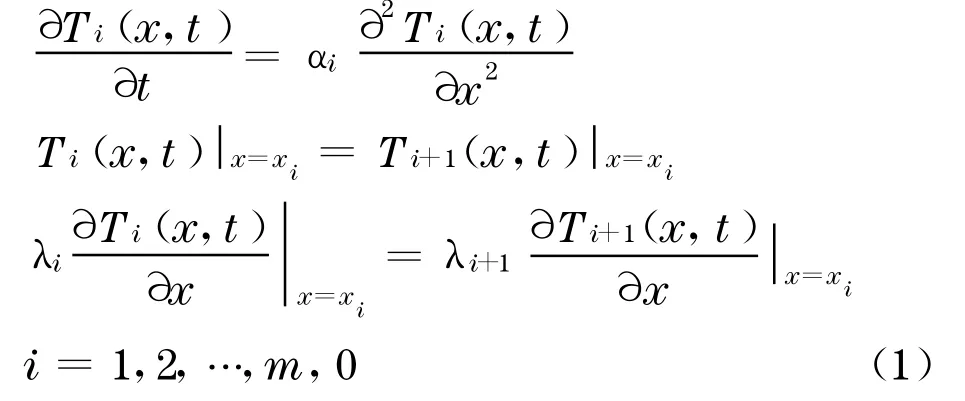
式中:αi,λi,hi分别为第i层路面结构层的导温系数、导热系数,结构层厚度;x为计算点距路表深度;t为时间.参见图1.

图1 路面结构示意图Fig.1 Schematic o f pavem ent structu re

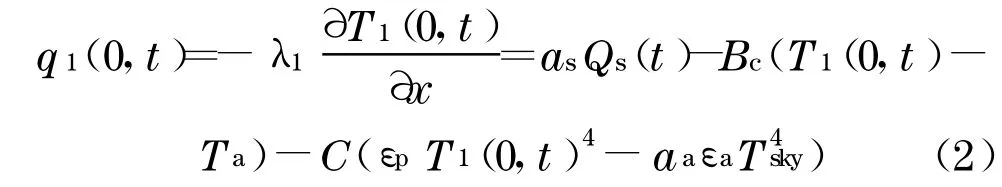
式(2)等式右边第一项a s Q s(t)为路面吸收太阳辐射能,其中,αs是路表对太阳辐射的吸收率,水泥混凝土路面为0.72～0.78,沥青路面为0.86～0.90;Qs(t)为太阳辐射强度,可表示为

式中:f为云、水汽、浮尘等影响的折减系数;Q0为太阳辐射常数(1 353 W·m-2);h⊗为太阳髙度,与地理纬度、太阳赤纬以及时刻有关.

式(2)等式右边第二项Bc(T1(0,t)-Ta)是路面与空气热对流交换的热流损失量,其中,Ta为气温,Bc为地气传热系数,它与风速、空气湿度等因素有关,一般变化在18～26W·m-2·K-1之间.

求解偏微分方程(1)需己知初始时刻t=0的路面温度Ti(x,0),以及路表边界的温度T1(0,t)或路表热流q1(0,t).路表热流q1(0,t)主要由3部分构成:太阳辐射、路面与空气热对流交换、路面与天空的相互辐射,即为路面与天空相互辐射的热流损失量,其中,C为黑体辐射常数=5.673×10-8W ·m-2·K-4;εp为路面辐射发射率,其值在 0.60～0.66之间;αa路表长波吸收率,约为 0.82～0.88;εa为天空辐射发射率,其值在0.87～0.91之间;Tsky为天空有效温度.

在已知路面温度初值Ti(x,0)和路表边界温度T1(0,t)或热流q1(0,t)条件下,偏微分方程(1)可用有限差分法求解[4-5].将路面沿深度x方向按间距Δx分割为m段,并保证路面各层的交接面有分割点,沿时间 t方向按步长 Δt分割为n段,从时间t=0开始,每段间隔为Δt,向前差分,则偏微分方程(1)离散为

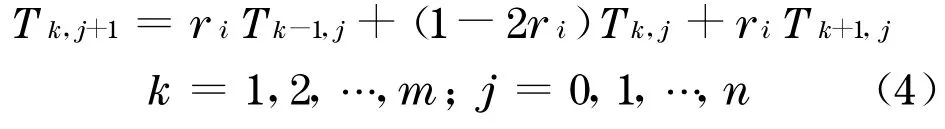
式中:ri为步长比,ri=αiΔt/Δx2.

对于已知路表温度的边界节点T1,j,则有

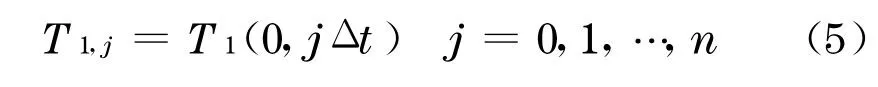
已知路表热流的边界节点 T1,j,可根据热平衡关系进行离散

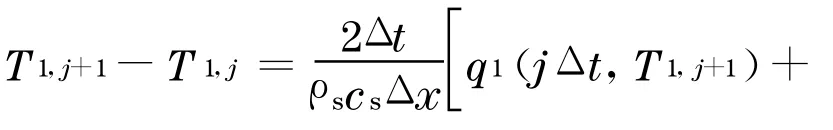
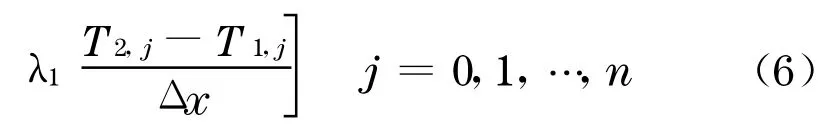
式中:ρs,cs分别为路面表层材料的密度和热容量系数.

当步长比r≤0.5时,上述差分格式是稳定收敛的.下面通过2个有理论精确解的均质半无限体已知表面温度T(0,t)和表面热流q1(0,t)呈正弦周期变化的例子,了解差分网格划分细疏程度以及步长比对数值解精度的影响.差分网格划分细疏程度用一个周期内单位深度范围的差分网格数N来表征,即

式中:A为周期长度,在例子中取24 h;n为一周期内的时间步长数.

计算表明,在已知表面温度时,半无限体温度数值解的最大误差出现在深度0.1 m附近,而己知表面热流时,数值解的最大误差出现在表面.图2为不同步长比r条件下差分网格数N与相对于精确解振幅的数值解最大误差的关系图,其中,α取0.002 8 m2·h-1,λ取1.3W·m-1·K-1.从图2中可以看到,已知表面温度的差分数值解比己知表面热流的差分数值解收敛快;步长比r在0.15～0.20时的数值解收敛速度最佳;步长比r为0.20且已知表面温度的场合,N≥90时,数值解计算误差可控制在1.0%,N≥2 800时,误差可控制在0.1%;而在已知表面热流场合,N≥1 200时,数值解计算误差可控制在1.0%,N≥36 000时,误差可控制在0.1%.因此,在以下的分析计算中,步长比r取0.20,时间步长Δt取2 min,即n=720(N≈36 000),以保证差分数值解的精度.

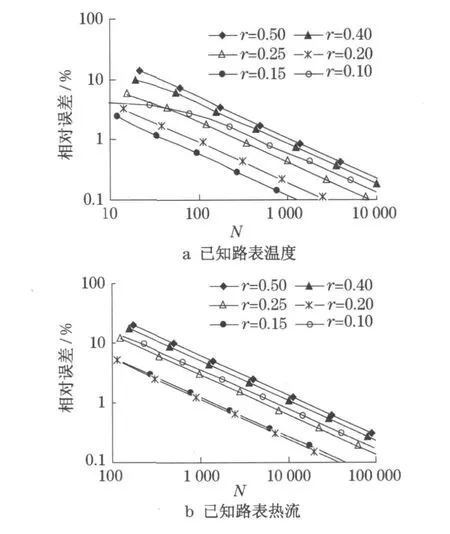
图2 差分数值解的误差图Fig.2 Error o f the finite differencem ethod

2 层状路面结构简化的误差

文献[2-3]认为一般路面结构材料的导热性能差别不太大,在不设隔热层条件下,可引入结构层厚度的导热系数当量变换,将多层路面结构温度场求解简化为均质半无限体的热传导问题.下面通过考察己知路表温度、己知路表热流条件下,典型水泥混凝土路面和沥青路面简化为均质半无限体所带来的偏差,以了解均质半无限体简化的适用范围和精度.

典型水泥混凝土路面和沥青路面结构的示意图见图3,在设炉渣隔热层或聚苯乙烯(EPS)隔热层时,假设隔热层设在基层下方,厚度为0.1m(图3中虚线位置),原石灰土垫层厚度由0.3 m减为0.2 m,各结构层的材料导热、导温系数见表1[6-7].分别按层状结构和简化半无限体计算已知路表温度、热流正弦周期变化条件下路表及各结构层层底(见图3中的A,B,C,C1,D点)的最高、最低温度与相位角.计算结果表明,按简化半无限体得到的路面结构各特征点的最高、最低温度值与层状结构特征点的最高、最低温度值之间的偏差不太大,它们之间的最大相对温度偏差(最高温度差与最低温度差的大者与路表温度振幅之比),除设EPS隔热层之外,均不超过4%,设EPS隔热层时也不大于10%,见图4,5;简化半无限体的各特征点相位角与层状结构的相位角对应的时间偏差,面层的最大偏差仅0.2 h左右,基层的最大偏差也不大于1.0 h,EPS隔热层及垫层的相位角偏差较大,最大可达4.0～6.0 h.上述结果表明,在路面温度场精度要求不太高及未设如EPS等高效隔热层时,将多层路面结构温度场求解简化为半无限体的热传导问题是基本可行的,但若釆用如差分法等数值解时,可直接分析层状结构的热传导问题,而不需将其简化为均质半无限体.

图3 典型路面结构及特征点示意图Fig.3 Typical pavem ent structure and calculating location s

表1 路面结构的材料导热系数、导温系数Tab.1 Heat conductivity and therm al conductivity coefficients of road mater ia ls

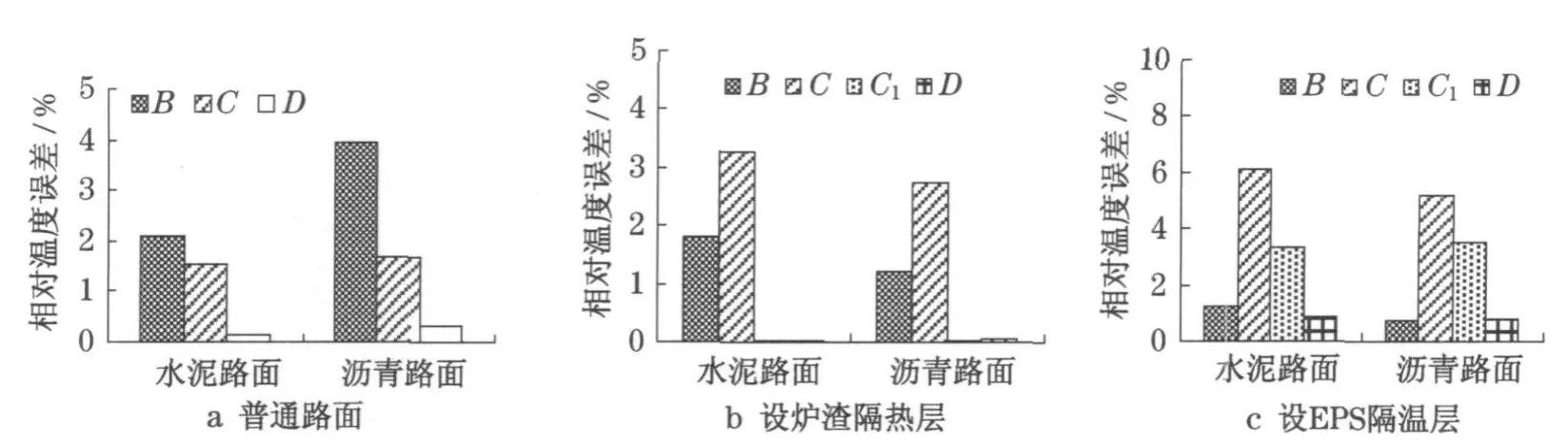
图4 半无限体简化的最大相对温度偏差(已知路表温度)Fig.4 Max relative temperature error of sem i-infinite body(given surface tem perature)

图5 半无限体简化的最大相对温度偏差(已知路表热流)Fig.5 M ax relative temperature error of sem i-in finite body(given surface heat f lux)

3 路面与天空相互辐射的简化误差

从式(2)可以看出,路面与天空相互辐射与路表温度 T1(0,t)和天空有效温度 Tsky的4次幂有关,所以偏微分方程是非线性,求解十分困难;在差分数值解时也需要通过求解一元四次方程才能得到路表温度T1(0,t).为了简化计算,文献[1]将路面与天空相互辐射在摄氏零度处作一阶泰勒近似

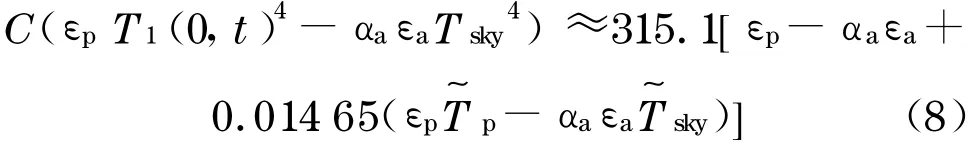
就目前的数值计算能力来看,这种为了避开求解一元四次方程而一阶近似是没有必要的.从下面的例子可以看到,这种近似处理方法会使路面最高温度与温度日较差(日最高温度与最低温度之差)偏大,其中,路表最高温度偏大超过1℃,随着深度加大,这种偏差有逐渐减少之势;路面结构各特征点的温度日较差均偏大3%左右,见图6.图6的计算条件为:太阳辐射按北京地区夏至时节晴天为基准,考虑云、水汽、尘埃等影响的太阳最大辐射强度fQ0取900W·m-2;气温Ta的日交变按正弦变化,日平均气温取20℃;日较差取10℃;天空有效温度Tsky取Ta-15℃;路面深度5 m处设为20℃恒温下边界;其他参数:Bc,αs,εp,αa,εa取第 1节中给出数值范围的中值.路面结构及参数同上节中的两种典型结构.

4 天空有效温度估计偏差的影响

地球大气层对短波为主的太阳辐射吸收率很低,但大气中二氧化碳、水汽、臭氧等对长波为主的地面辐射具有较强的吸收作用,这几种气体在吸收地表长波辐射的同时也不断向四周辐射能量,其中,指向地面的大气辐射称之为天空逆辐射.天空有效温度Tsky就是表征天空逆热辐射总量的温度参数.它与所在地区的时(季节)空(纬度、海拔)、空气湿度和云量等因素有关,当云层厚且低时,天空逆辐射以云层为主,Tsky接近气温;天气干燥且无云时,臭氧的辐射量比例增大,Tsky降低,向臭氧层温度靠近.有研究指出,我国的Tsky值与气温Ta的差值从南到北递增,夏季变化在-12～-16℃,冬季变化在-15～-27℃[8].

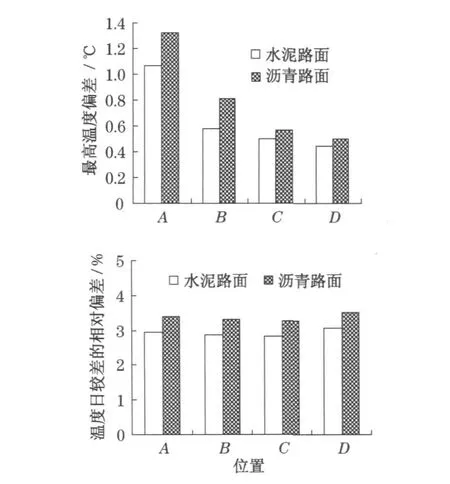
图6 路面与天空相互辐射的简化误差Fig.6 Error of pavem ent surface tem perature an d sk y ef fective tem peratu re

由于天空有效温度 Tsky的影响因素众多,且未列于气象监测项目,因此,其准确值难以确定.在有些路面温度场研究中,近似用气温Ta代替,这种近似方法是不能接受的,它会使路面温度计算值偏高.图7给出了天空有效温度 Tsky与气温 T a之差 ΔT(ΔT=Ta-Tsky)为10,20和 30℃时,天空有效温度Tsky与仍按气温Ta取值,造成的水泥路面(沥青路面的情况也相似)各特征点(其他参数同第3节的例子)最髙温度偏差值与温度日较差的偏差值.从图7中可以看到,天空温度 Tsky用气温Ta代替,会使路面结构的整体温度偏大,但对温度日较差的影响很小,路面最髙温度的偏差值随着ΔT值扩大而加大,其中,路表最髙温度偏差值与ΔT之比在15%上下;随着深度增加,最高温度的偏差量减小甚微,而温度日较差的偏差有扩大之势,也就是说,天空有效温度将给路面温度场带来全局性的不利影响.

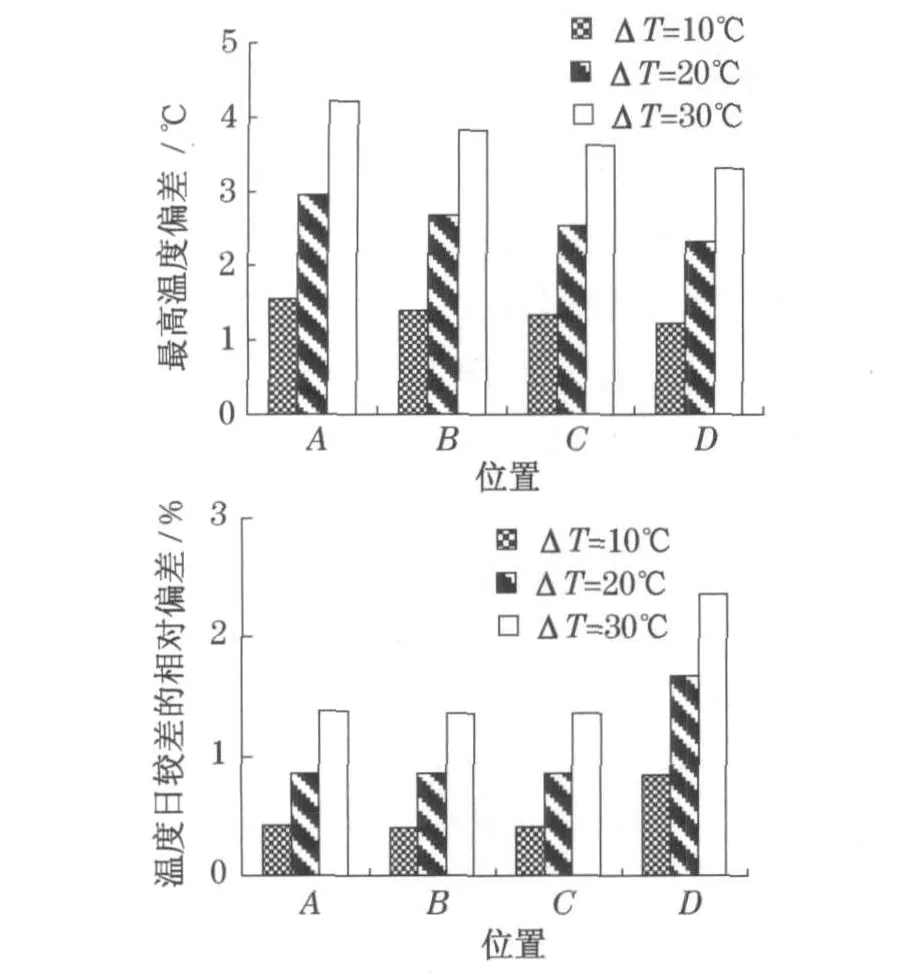
图7 天空有效温度估计偏差对水泥路面温度场的影响Fig.7 Effects of estimated error o f sky effective temperature on tem perature field of cement concrete pavem ent

5 初始温度偏差的影响

应用差分法求解非稳态路面温度场,需已知初始时刻的路面温度沿深度分布状况,即T(x,0)需已知.但在实际应用时,路表以下的温度初始分布是难以精确估计的.

对于上述两个典型路面结构,当路面深度在0～0.5 m及0.5～1.0 m范围内的初始温度估计偏差为±2℃,±5℃时,路面结构各特征点温度偏差小于允许偏差±0.2℃的消散历时,如图8所示.从图8可以看到,以允许偏差±0.2℃计,深度0～0.5m范围内温度偏差±2℃时,面层消散时间为2～3 d,基层为3～4 d,垫层为4～5 d;温度偏差增至±5℃时,各层的消散时间约比±2℃时的消散时间增大一倍;同初始温度偏差量条件下,0.5～1.0 m范围内温度偏差的消散时间比0～0.5 m范围内温度偏差的消散时间多一倍.由此可见,路面温度初始值的估计偏差对路面温度场影响会随着时间的增加而渐渐变小,在相同误差范围条件下,深度越浅,温度初始值的估计偏差的不利影响消散越快.

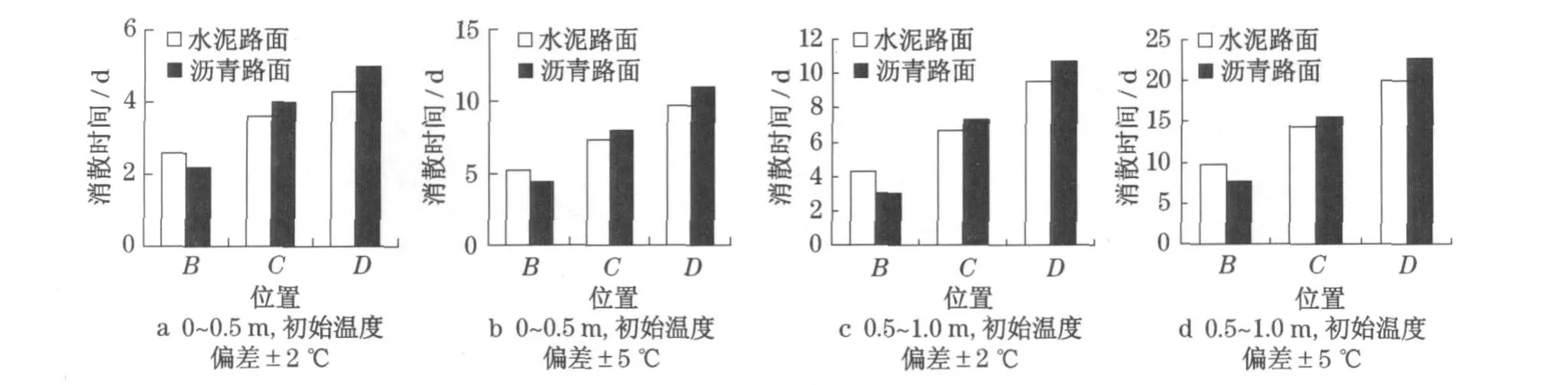
图8 温度初值偏差的消散历时图Fig.8 Dispersing tim e of initia l tem perature error

6 结论

(1)釆用有限差分法求解路面温度场是合适的,其步长比r取0.2左右时收敛速度最佳,时间步长Δt取2min,数值解计算误差基本可控制在0.1%之内.

(2)未设如EPS等高效隔热层的路面结构,其温度场求解简化为半无限体热传导问题是基本可行的,偏差不大于4%.釆用差分法等数值解时,可直接分析层状结构的热传导问题,不需将其简化.

(3)为避开求解一元四次方程而将路面与天空相互辐射项中的路表温度T1(0,t)和天空有效温度Tsky的4次幂关系作一阶近似没有必要,它会引起路面最高温度与日较差偏大.

(4)天空有效温度T sky不能用气温T a代替,否则会使路面温度计算值偏高,温度日较差的偏差随深度增加有扩大之势.由于天空有效温度不是气象检测项目,因此,准确地估计天空有效温度将成为路面温度场研究中关键问题之一.

(5)温度初始值的估计偏差对路面温度场的影响可随着时间的增加而渐渐消散,深度越浅消散越快.以允许偏差±0.2℃计,深度0～0.5 m范围内温度偏差±2℃时,面层消散时间为2～3 d,基层为3～4 d,垫层为4～5 d;温度偏差增至±5℃时,各层消散时间约增大一倍;温度偏差相同条件下,0.5～1.0 m范围内温度偏差的消散时间比0～0.5 m的多一倍.

[1] 姚祖康.水泥混凝土路面设计[M].合肥:安徽科学技术出版社,1999.YAO Zukang.Cem ent concrete pavemen t design[M].Anhu i:Anhui Science and Technology Press,1999.

[2] 严作人.层状路面温度场分析[D].上海:同济大学路桥系,1982.YAN Zuoren.Analysis of temperature field in mu lti-layer pavement[D].Shanghai:Tongji Un iversity.Department of Pavement and Bridge Engineering,1982.

[3] Barber E S.Calculation ofmaximum pavem ent temperature from w eather repor ts[R].Washing ton D C:National Academy of Sciences NationalResearch Council,1955.

[4] 章熙民,任泽霈,梅飞鸣.传热学.[M].第4版.北京:中国建筑工业出版社,2001.ZHANG Xim in,REN Zepei,MEIFeim ing.Heat transfer[M].4th ed.Beijing:China Architecture and Building Press,2001.

[5] Ake H.Simu lation model for calculating pavem ent temperature inc luding maximum temperature[J].T ranspor tation Research Record,2000(1699):134.

[6] 吴赣昌.半刚性路面温度应力分析[M].北京:科学出版社,1995.WU Ganchang.Analysis of sem i-rigid pavemen t temperature stress[M].Beijing:Science Press,1995.

[7] 谈至明,孙立军.路面结构低温状况分析[J].同济大学学报:自然科学版,1999,27(5):520.TAN Zhim ing,SUN Lijun.Low temperature condition of pavement structure[J].Journal of Tongji University:Natural Science,1999,27(5):520.

[8] 刘森元,黄远峰.天空有效温度的探讨[J].太阳能学报,1983,4(1):63.LIU Senyuan,HUANG Yuanfeng.Discussion on effective sky temperature[J].Solar Journal,1983,4(1):63.