阵列天线相位中心的计算与分析

陈 曦 傅 光 龚书喜 阎亚丽 栗 曦

(西安电子科技大学天线与微波技术国家重点实验室,陕西西安710071)

1.引 言

目前,相控阵天线已经被广泛的应用于各种雷达系统,并且随着对雷达系统的跟踪、定位精度的要求越来越高,在VHF及以下频段,单靠波束幅度特性进行搜索定位已不能满足要求,必须以天线阵的相位中心为基准进行精确定位和测量[1]。对于寻找天线相位中心的研究,前人得到了一些有效的方法,但大多数都是针对单天线的研究[2-5],像文献[5]中的研究,作者通过多次尝试,反复测量,最终找到相位中心,这对于小体积天线是可行的,但对于数个波长尺寸的阵列天线,则希望减少调整的次数。目前,国内关于阵列天线相位中心的研究甚少,文献[6]中曾有提及,作者在研究对数周期天线的相位中心时,对直线阵的相位中心存在的条件进行了研究,得到一些有意义的结论。国外在十多年前有过一些阵列天线相位中心的研究,1990年,Helaly和Shafai曾在文章[7]中推导出理想线阵的相位中心的表达式,该法在实际天线应用中会有其局限性,但不妨碍得出单元幅相激励失效时相位中心的变化规律。

本文将以阵列分析理论为基础,推导出阵列天线相位方向图与相位中心的关系式,并基于这一关系式,得出寻找阵列天线相位中心和视在相心的方法和结论,重点放在视在相心的求解上;并通过数值模拟实验对其进行仿真验证,以证明方法的有效性和实用性。

2.阵列理论

下文中,笔者将从实验调整的角度考虑进行阵列天线建模和理论分析。

一般情况下,阵列天线源点和场点的空间分布如图1所示。假设阵列天线工作或者测试的初始状态位于任意位置1,阵列上的第q个单元在远场区的电场主极化分量可表示为

图1 阵列天线位置调整及辐射场示意图

式中：C是比例常数;A(q)、φ(q)是第q个单元激励的加权幅度和相位;F(q,ro)是第q个单元的远场方向图,包含单元的幅度和相位信息;波数是单元q到场点的距离是r方向的单位矢量是电场主极化分量的单位向量,且有uo◦ro=0。

如果所有单元的主极化分量方向一致,对所有单元的辐射场矢量求和可得到阵列的总辐射场。单元之间的互耦影响可以通过折算为单元激励加权和单元方向图的扰动加以考虑。依此得到的辐射总场是精确的也是复杂的。通常对其进行近似简化,以利于得到有效的结论。

如果阵列单元相同,且单元方向图近似不变,则F(q,ro)=F(ro);对于辐射远场区,相位项中,r-ρq◦ro[8],其中ρq是第q个单元在选定坐标系下的位置矢量;距离项中,因此,总辐射场的主极化分量可表示为

将阵列从位置1移动到位置2,设移动矢量M(方向为1指向2)。相当于阵列中每个单元被移动M,此时总场的主极化分量可表示为

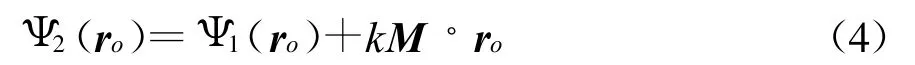
这与在单天线中得到的相位方向图变化规律是一样的,这是因为当场点距源点的距离为无限远时,阵列天线的大尺寸就可以被忽略,与单天线相差无几。但随着距离变为有限,阵列的尺寸不能忽略,式(4)就不再严格成立。由于实际中的雷达天线都是工作在有限距离远场,所以这种分析是有其实际意义的,需进一步深入研究。

3.阵列天线的相位中心

3.1 阵列天线相位中心和视在相心的定义

阵列天线相位中心和单天线相位中心的定义基本相同,即在阵列天线上或其周围找一个参考点,该点可使远区辐射场的某个区域内的相位值是一常数,称该参考点为阵列天线的相位中心。通常所关心的区域是主瓣的半功率波瓣宽度(HPBW)。阵列天线和单天线方向图最大的差异就是HPBW,通常都在十几倍以上。

而实际上,除了点源外,任何天线都不可能使远场相位值是一个常数。这是因为任何实际天线都由无数点源构成,虽然从远场观察可以近似等效为一个点源,但这与场点到源点的距离、天线的口径场分布有很大关系;另一方面,实物天线与理想天线相比一定存在各种误差,如加工误差、装配误差、测试误差等,这是不可避免的,也无需完全避免。因此,通过测试或计算得到的相位值不会是常数。但在满足工程应用的条件下,可以给出一个可实际操作的获得等相位面的相位中心定义。如找到一个参考点,使远场主瓣HPBW内的相位值变化最小,则称该参考点为视在相位中心,简称“视在相心”。通常会应用方向图不同截面内的二维视在相心,并且不同的截面内会得到不同的二维视在相心,这是因为天线在不同截面内的口径场分布一般不同。这也可以解释为什么一般天线的辐射场都不是理想的球面波。反之如点源,在不同截面内的口径场分布相同,所以可以得到唯一的视在相心。相位值变化最小可以通过数学方法加以衡量,比如使相位最大最小值的差最小,或者求在最小二乘意义下的最小值。文献[9]曾用最小二乘法求出单天线的视在相心所在,并达到较好的效果。

阵列天线和单天线对于相位中心和视在相心定义相差不大,最大的区别在于阵列天线不仅包括阵单元的特性,同时还包括阵因子的特性,如阵元数、单元间距、激励分布以及互耦等。这会使得整个天线的场特性的受制因素更多,会引入更多的误差,但在无限远场下,阵因子特性容易被忽略。

3.2 相位中心的求法

根据相位中心的定义,可以令式(4)中 Ψ2(ro)=C,可得到

在直角坐标系下,式中的矢量可以表示为

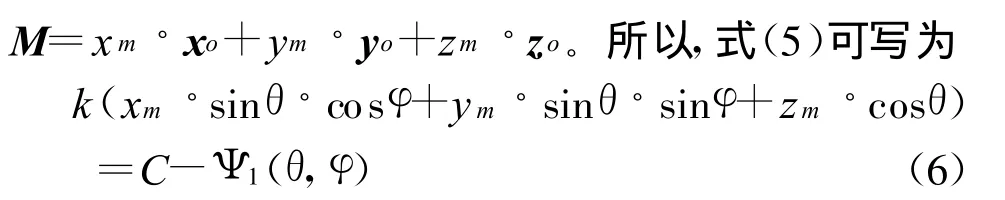
若口面电场的极化方向沿x轴方向或y轴方向,对于关注的主平面,即φ=0°或90°,式(6)可简化为如下表达式。其中 φ=0°时,tm=xm;φ=90°时,tm=ym。

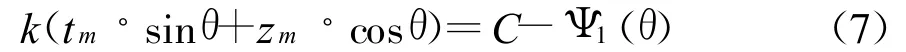
式(7)包含三个未知数,因此只需知道关注区域内的任意三个角度和对应的相位值,便可求出相位中心。如主瓣宽度为BW,最大指向为θm,则根据式(7)可得到

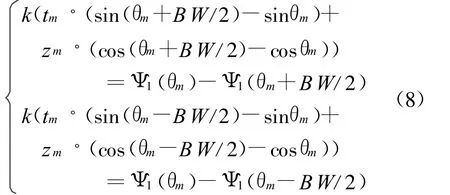
求解该线性方程组便可得到相位中心。

3.3 视在相心的求法

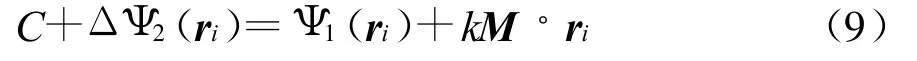
求出使ε最小的M值,即得到视在相心所在。

直角坐标系下主平面内的表达式为

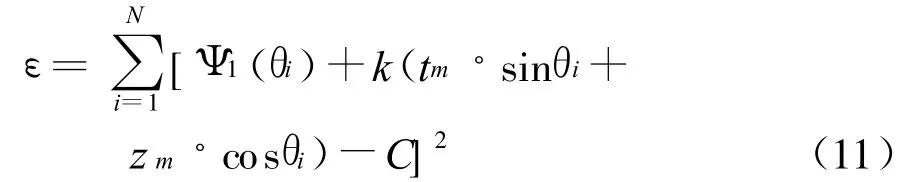
同样,φ=0°时 ,tm=xm;φ=90°时 ,tm=ym。式(11)式两边分别对和C求导,并令其为0,可得式(12)。解该线性方程组可得到视在相心。通常情况下,在不同截面内求得的不相同,要得到三维视在相心可以求出不同的算数平均值。

4.数值结果

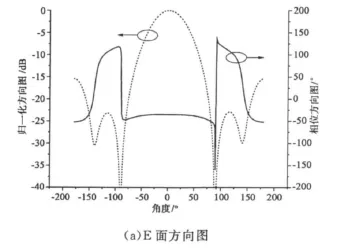
为验证阵列天线视在相心算法的有效性,应用电磁仿真软件HFSS对一个14×20的平面栅格阵列进行仿真。图2是阵列结构示意图。阵列单元采用带有限尺寸反射板的对称振子,当坐标系原点取在单元相位中心附近时,对应的E面(x-z面)和H面(y-z面)幅度和相位方向图如图3所示。其中E面的HPBW为63.35°,根据这个角度范围内的相位分布可求得视在相心位于 xm=0.00088402λ,zm=-0.010296λ,意为沿对应坐标轴调整相应距离,负号为沿负向移动;H面的HPBW为84.54°,视在相心位于 ym=0.00036795λ,zm=0.01843λ。显然,E面和H面的视在相心不完全重合,这是预料中的,因为单元在不同截面内的口径场分布并不相同。但综合考虑zm的调整量,可认为阵列单元的三维视在相心已位于坐标系原点。另外,从图3可以很直观的看到,随着角度范围的变化,相位值的平坦度也会变化。

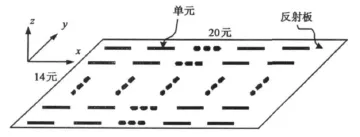
图2 阵列结构示意图

阵列沿俯仰向(y轴)和方位向(x轴)分别采用14个和20个单元,俯仰向和方位向的单元间距分别为 0.567λ,0.454λ。不考虑单元间互耦对方向图的影响。为了验证视在相心算法的有效性,在仿真初期,假设阵列天线的视在相心在直角坐标系下存在偏移量(0.5λ,0.5λ,0.5λ),可得到图4 所示的阵列天线方向图。其中,E面HPBW为 6.30°,H面HPBW为 7.25°。显然,对应区域内的相位值非常不平坦。通过计算得到：E面的视在相心位于=-0.49932λ,=-0.50515λ;H 面视在相心位于ym=-0.49979λ,zm=-0.45912λ。调整后的视在相心列于表1中。综合考虑,阵列三维调整量为(-0.5 λ,-0.5 λ,-0.48 λ),调整后的方向图如图5所示,HPBW内的相位分布已经很平坦了。为了得出阵列方向图和单元方向图的联系,再次计算单元E面主瓣 6.30°内的视在相心,以及H 面主瓣7.25°内的视在相心,这与在较宽的角域内计算的结果是不同的,比较列于表1。与阵列E面和H面内的视在相心相比较会发现,阵列在HPBW内的视在相心主要由其单元在该角域内的视在相心决定,并且对于阵列单元来说,不同的角域对应不同的视在相心。因此,当相控阵进行波束扫描时,波束宽度和波束指向都会变化,视在相心也会相应发生变化。需要注意的是,这一结论是在无限远场条件下以及不考虑互耦时得到的。

表1 单元和阵列不同角域对应的视在相心比较

4.结 论

本文从阵列理论分析入手,推导出了无限远场条件下,相位方向图和参考点选取的关系。并对阵列天线相位中心和视在相心的定义从性质上加以区分,进而根据定义给出相位中心和视在相心的严格推导和表达式。根据得出的结论,对一个矩形栅格平面阵进行的仿真实验,证明了本文得出的阵列天线视在相心算法是有效的。同时发现,阵列天线在主瓣的HPBW内相位方向图对应的视在相心主要决定于阵列单元在这一区域内相位方向图对应的视在相心。并且,阵列单元的视在相心也随关注角域的变化而变化。可以预见,当相控阵天线进行波束扫描时,阵列天线主瓣HPBW会变化,同时阵列单元的相位分布也随扫描角变化,所以,需要进一步对该情况下的视在相心分布及变化进行研究。另一方面,当远场不再是无限远时,阵因子特性对相位分布的影响会加以体现,情况也会更加复杂,这也是需要深入研究的一个方面。

[1]MOHEB H,SEBAK A,SHAFAI L.Phase centre analysis of array antennas and its significance for microwave landing system[C]∥Seventh International Conference on Antenna and Propagation(IEE).York,UK,1991：213-216.

[2]CRUZ J L,GIMENO B,NAVARRO E A,et al.The phase center position of a microstrip horn radiating in an infinite parallel-plate waveguide[J].IEEE T rans on AP,1994,42(8)：1185-1188.

[3]MUEHLDORF E I.The phase center of horn antennas[J].IEEE Trans on AP,1970,18(6)：753-760.

[4]金元松,董明玉,何绍林,等.对数周期偶极子天线的可变相位中心[J].电波科学学报,2001,16(3)：323-328.JIN Yuansong,DONG Mingyu,HE Shaolin,et al.The variable phase center of the log-periodic dipole antenna[J].Chinese Journal of Radio Science,2001,16(3)：323-328.(in Chinese)

[5]唐 璞,李 欣,王 建,等.计算天线相位中心的移动参考点法[J].电波科学学报,2005,20(6)：725-728.TANG Pu,LI Xin,WANG Jian,et al.Calculation of phase center for the antenna with the method of moving reference point[J].Chinese Journal of Radio Science,2005,20(6)：725-728.(in Chinese)

[6]金元松,任晓飞,冀海鸣,等.对数周期偶极子天线全空间可变相位中心[J].电波科学学报,2007,22(2)：229-233.JIN Yuansong,REN Xiaofei,JI Haiming,et al.Variable phase center of the log-periodic dipole antenna in full space[J].Chinese Journal of Radio Science,2007,22(2)：229-233.(in Chinese)

[7]HELALY A,SEBAK A,SHAFAI L.Phase center movement in linear phased array antennas[C]∥Antennas and Propagation Society International Symposium,1990,3：1166-1169.

[8]MAILLOUX R J Phased Array Antenna Handbook,Second edition[M].US：Artech house inc,2005：9.

[9]尚军平,傅德民,邓颖波.天线相位中心的精确测量方法研究[J].西安电子科技大学学报,2008,35(4)：673-677.SHANG Junping,FU Demin,DENG Yingbo.Research on the accurate measurement method for the antenna phase center[J].Journal of Xidian University,2008,35(4)：673-677.(in Chinese)

[10]梁昌洪.从实验数据处理谈起[M].西安：西安电子科技大学出版社,1996：18-19.