在新课程背景下教师应具有怎样的“一桶水”——由单摆教学所想到的
黄鹤松
(江苏省启东中学,江苏启东 226222)
在教与学的关系中,人们经常提到“一杯水”与“一桶水”的问题.单摆是振动教学中一个重要内容.下面笔者以单摆教学为例谈谈教师应有怎样的“一桶水”.
1 教师的“一桶水”应广而多
我们从知识的广度上畅想一下与单摆有关的内容.
一根不可伸长的不计质量的绳一端固定,另一端系一质点便形成一个理想的单摆(也叫数学摆).
单摆在摆角小于5°(新教材放宽到 10°)情况下所做的无阻尼振动可以看作简谐运动,摆球可看作为谐振子.
单摆长时间的摆动,其摆动平面将会缓慢转动,这是因为摆的运动可以超然于地球的自转,但悬挂摆的支架一般要带动它参与地球的自转.150多年前的傅科摆实验已经让人们体会到了地球的自转.由于我们讨论的单摆摆动时间较短,故不考虑单摆摆动平面的缓慢转动.
单摆的等时性由科学家伽利略首先发现.
单摆的周期公式由荷兰科学家惠更斯推导出来,他还设计了世界上第一个摆钟,并申请了专利.因此从某种意义上讲,我们大量工厂所生产的摆钟产品应向惠更斯这位科学家支付专利费.
从单摆的等时性联想到时间及单位本征时间的定义.古人以脉搏跳动来定义单位时间,也有以滴水间隔为时间单位,更有利用漏沙进行计时.各种记时方法有一个共同点:找一个恒定的时间间隔来定义单位时间.但上述这些计时方法中的时间间隔都不够恒定.随着科学的发展,近代人们以地球自转时间作为一个恒定的时间间隔,这一记时方法比“脉搏”、“滴水”及“漏沙”精确多了.但后来人们又发现,由于空气等一些因素的存在,地球自转的周期在逐渐减小,地球自转的不均匀性使得天文方法所得到的时间(世界时)精度只能达到10-9s,无法满足20世纪中叶社会经济各方面的需求.随着人们对记时精度要求的不断提高,一种更为精确和稳定的时间标准应运而生,“原子钟”以一定数量的原子精细跃迁(到目前为止所能找到的最恒定时间间隔)为恒定时间间隔而确定单位本征时间“秒”.
……
新课程要求教师的知识面是宽广的,才能在教学中做到信手拈来,同时也能对学生起到引领示范的作用,引导学生走向知识的海洋.
2 教师的“一桶水”应精而深
我们从知识的深度上拓展一下与单摆有关的内容.高中阶段在单摆的教学中有一类摆钟走时问题,有难度.笔者认为解决该类问题应找准切入点,注意其特性.这个切入点便是摆钟的显示时间.
当一个摆钟做好以后,机械装置中的传动部分已不可能发生变化.换句话说同一摆钟的机械传动特性不会改变.
摆钟所显示的时间与摆钟振动的次数成正比,令钟摆一次全振动的显示时间为t0秒,则钟摆振动n次显示时间为

同样的道理摆钟走过的真实时间也与钟摆振动的次数成正比,令钟摆一次全振动的真实时间为 T0秒,则摆钟振动n次真实时间为
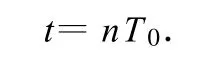
这两个式子便是解决摆钟走时快慢问题关键.下面通过例子具体讨论 .
若已知北京的重力加速度 g北=9.801 m/s2,南京的重力加速度 g南=9.795 m/s2,把在北京每小时慢10 s的摆钟拿到南京,问该钟在南京一昼夜的走时误差是多少?
先讨论“北京”,设该钟摆在北京做一次全振动的时间为 T北,该摆钟做一次全振动的显示时间为 t0.
根据题中所述,“北京钟”真实过了 3 600 s,该钟显示(3 600-10)s,则有

再讨论“南京”,设该钟摆在南京做一次全振动的时间为 T南,该摆钟做一次全振动的显示时间为 t0(此值永远不变).并设该摆钟在南京每 3 600 s走时误差为Δt.则有

又如一钟摆摆长为 L1时在 t时间内走时快了 Δt,摆长为L2时在t时间内走时慢了Δt,问摆长多长时该摆钟走时正确?
也可用上面所述的公式解题.
先讨论“快钟”,并设该摆钟做一次全振动的时间为T1,该摆钟做一次全振动的显示时间为 t0.则有该“快钟”在t时间内的显示时间为

再讨论“慢钟”,并设该摆钟做一次全振动的时间为T2,该摆钟做一次全振动的显示时间为 t0(此值永远不变).则有该“慢钟”在 t时间内的显示时间为

最后讨论“走时正确钟”,显然有显示时间等于正确时间,即
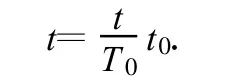
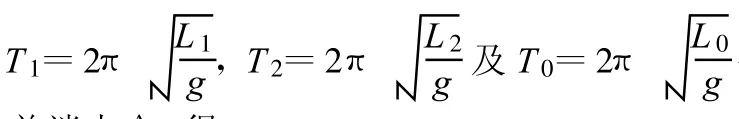

上述两个例子有一定深度,但未超出教学大纲.对于重点高中理科班的学生而言属于需要掌握的内容,但如在新课阶段立即引入,不符合学生的认知规律,笔者建议放在高三复习阶段加以拓展.
下面关于单摆的内容超出了物理教学大纲.
惠更斯所设计的摆钟钟摆的每个部分都有质量,不是一个理想的单摆,而是一个复摆.我们可以简化为如图1所示的情形,即由一根长为L的刚性轻杆,在杆的外端点和杆的中点放两个质量均为m的小球,组合成的复摆做振幅很小的自由振动.下面试着推导一下该复摆的振动周期.
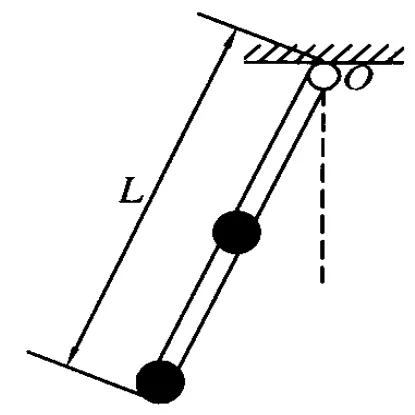
图1
复摆这一物理模型属于大学普通物理学的内容,由于中学阶段知识的局限性,不能直接求解.但我们可以利用“等效法”,将其转化成中学生熟悉的单摆模型,求出该复摆的等效摆长,便可求解周期.
设想有一摆长为 L0的辅助单摆,其摆球的质量为 M,与复摆周期相等,两摆分别从摆角α处从静止开始摆动,摆动到与竖直方向夹角为β时,具有相同的角速度ω,对两摆分别应用机械能守恒定律列出方程.
对复摆列出机械能守恒方程有
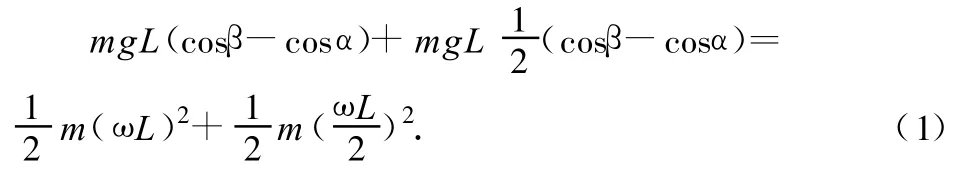
对辅助单摆,也列出机械能守恒方程
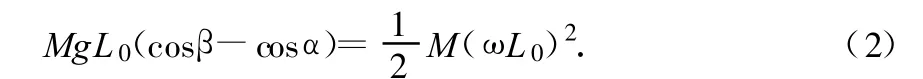
(1)式除以(2)式,得等效摆长
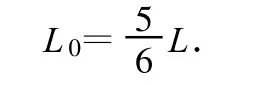
故复摆的周期为

由以上分析可知,钟摆的摆虽然是复摆,但周期规律仍可用等效摆长的单摆周期公式处理.
新课程要求教师对专业知识的掌握是精深的.我们教师只有具备了精深的专业知识,才能使教学过程充满睿智,才能引领我们的学生进入学科高端,为国家培养基础研究人才.

