基于体系结构的软件可靠性模型的统一框架

丁明丽，王海瑞

0 引言

在过去几十年中，软件可靠性研究主要集中在对黑盒模型上，把软件系统看成一个整体只建模它与外界环境之间的交互，而不考虑它的内部结构。Hamlet[1]，Horgan[2]等指出了这种黑盒方法的缺点，包括它们只能应用于软件生命周期的后期，忽略了组成系统的构件的测试以及可靠性信息，没有考虑软件的体系结构，因此需要实现在软件应用生命周期早期考虑应用体系结构以及组成构件的测试和可靠性信息来预测应用的可靠性。

Goseva-Popstojanova[3]等把目前提出的基于体系结构模型分为 3 类：基于状态的模型，基于路径的模型和可加模型。本文构建了基于体系结构的软件可靠性模型的统一框架，用来实现对基于体系结构的 3 类模型的分析比较。在上述 3 类模型中，基于状态的模型提出最早也研究最多，是目前提出模型种类最多的一类模型。本文建立的框架也是以基于状态的模型为核心结合其他两类模型。

1 基于体系结构的软件可靠性模型

使用基于体系结构的方法进行可靠性分析，需要如下2个方面的特征信息：

（1）应用的体系结构：

应用的体系结构表示软件中不同构件之间的交互方式，通常用构件之间的转移概率（由软件的运行剖面决定）表示。体系结构也可包括每个构件的执行时间信息（均值，方差，分布）。基于状态的模型中，应用的体系结构可建模为离散时间马尔可夫链（DTMC），连续时间马尔可夫链（CTMC）或半马尔可夫过程（SMP）。它们可进一步分为不可约的和吸收的，前者表示持续运行的应用，后者表示终止应用。任意时刻应用的状态由在该时刻执行的构件表示，状态转移表示构件之间的控制转移。基于路径的模型建模应用的体系结构为软件中所有可能的执行路径以及路径的执行概率。可加模型不考虑应用的体系结构。

（2）构件的失效行为：

基于状态的模型中，构件的失效行为可以采用3种方法建模：构件的可靠度，常量失效率，时间依赖的失效强度。假设构件失效之间相互独立，构件的可靠度为构件在一次执行过程中不发生失效的概率，不管构件是单独执行还是处于应用的上下文中执行。时间依赖的失效强度是某类软件可靠性增长模型的失效强度。根据三种失效模型结合信息的详细程度和生成可靠性预测的准确度，可以把它们排列成一个等级。当用可靠度建模构件的失效行为时，得到的应用可靠性估计的准确性最低。用常量失效率建模失效行为比前一种情况能提高可靠性预测的准确度，因为这种方法考虑了应用一次典型运行中构件被多次访问的总的执行时间。用时间依赖的失效强度来建模构件失效行为时能生成最准确的可靠性预测，因为它考虑了构件的测试及使用特征。基于路径的模型使用构件的可靠度或路径的可靠度来描述失效行为，可加模型使用时间依赖的失效强度来表示构件的失效行为。

将体系结构模型与构件的失效模型结合起来，计算得出应用可靠性估计值的方法为基于体系结构的模型的求解方法。基于状态的模型的求解方法包括两种：组合方法和等级方法。组合方法将应用的体系结构模型和构件的失效模型组合到一个模型中，然后对这个组合模型进行分析求解来预测应用的可靠性。等级方法先求解体系结构模型，然后将构件的失效行为加到体系结构模型的求解结果上，从而来预测应用的可靠性。给定应用的体系结构模型和构件的失效模型，组合方法能生成可靠性估计的精确值，而等级方法只能生成近似值。但是组合方法并不能应用于体系结构模型和构件的失效模型的各种组合中，只有当组合后的模型与原始的体系结构模型的类型一致时，组合方法才能使用。基于路径的模型和可加模型都只有一种求解方法。

2 统一框架

我们以基于状态的模型为核心建立基于体系结构的软件可靠性模型的统一框架。根据基于体系结构的模型的三要素：体系结构模型，构件失效模型，求解方法，对所有基于的状态模型的分类如表1所示。如果对应的模型存在，则在表格中标明了我们对模型自定义的名称，如果模型有文献出处也进行了标注；如果模型不存在，用“×”表示。

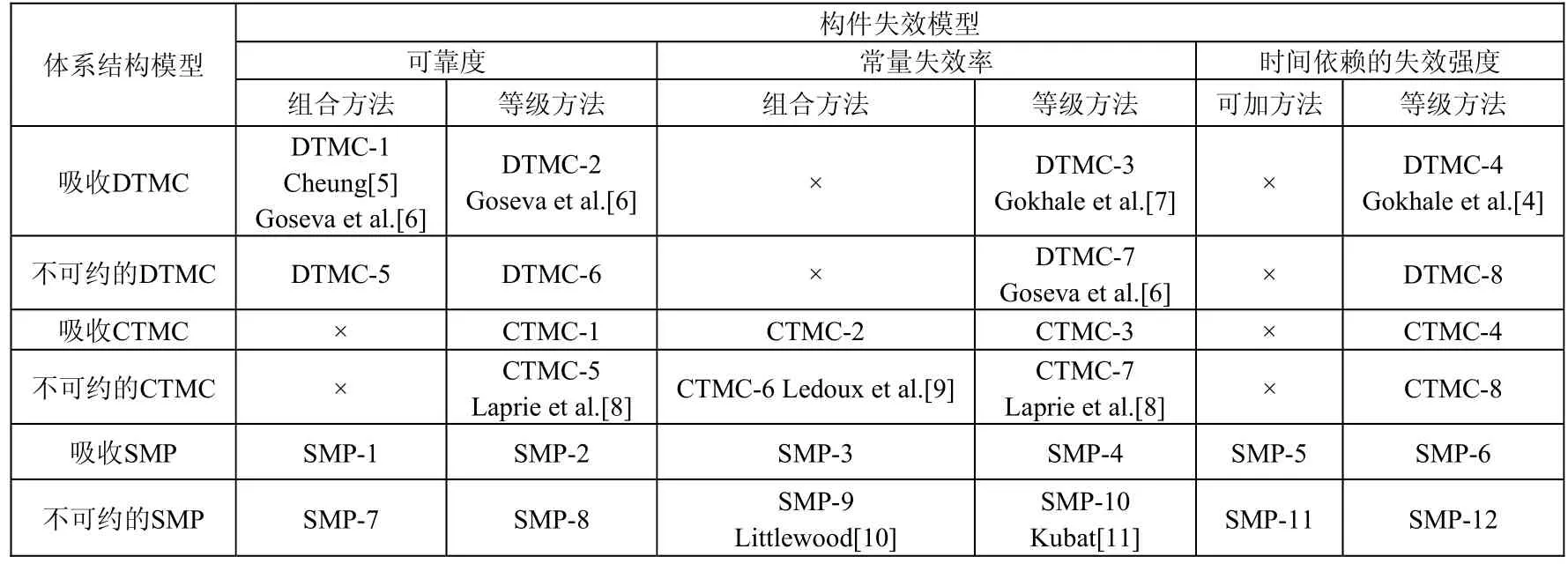
表1 基于状态的模型

下面针对具体的软件应用对表1中的基于状态的模型进行讨论，与基于路径的模型和可加模型进行比较分析，建立基于体系结构的模型的统一框架。对将用到一些符号注释如表2所示。

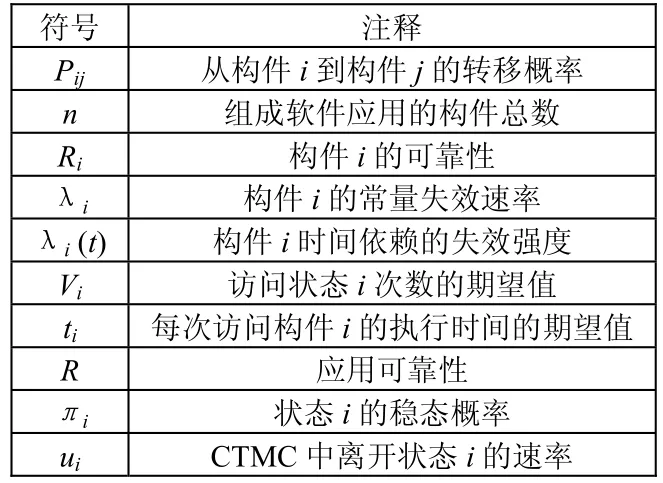
表2 符号注释

2.1 终止应用

对于终止应用，可靠性度量为应用一次典型执行的可靠度。终止应用的体系结构可建模为吸收的Markov模型。由表1可以看出，对于终止应用，相关文献中建模应用的体系结构为吸收DTMC。原因是用吸收CTMC或吸收SMP建模时，在求解过程中也是利用它们内嵌的DTMC进行求解的。对于硬件系统来说，认为所有构件处于持续激活状态，因此系统可靠性可以表示为

而对于软件系统来说，构件在调用时执行，一个关键问题是考虑应用执行过程中构件的使用情况。对吸收 DTMC进行分析，可以得到应用一次典型执行过程中访问每个构件次数的期望值Vi。Vi表示终止应用执行过程中构件的使用情况。当使用不同的构件失效模型，得到应用一次典型执行过程中构件的等价可靠度以及整个应用的可靠度如表3所示。

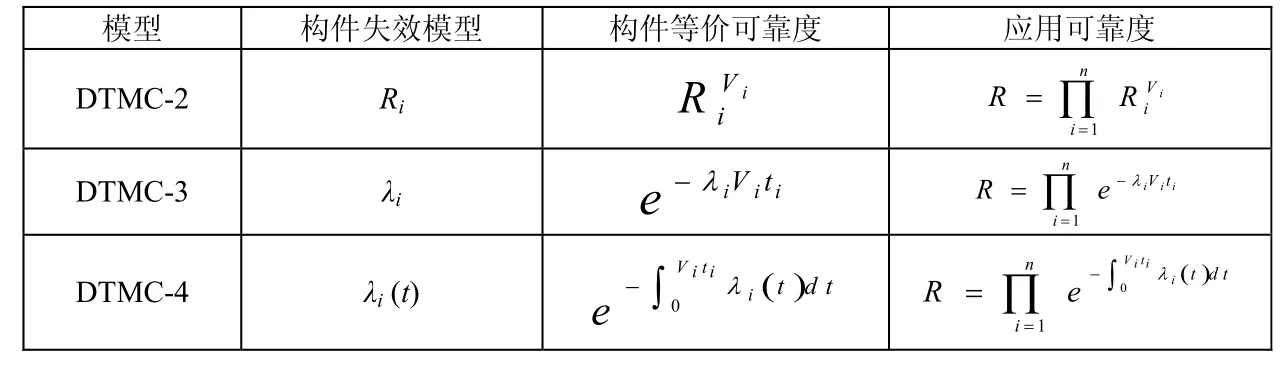
表3 终止应用可靠性分析

表3中的模型采用的求解方法为等级方法。DTMC-1模型使用的是组合方法，组合模型由应用的体系结构模型和组成软件应用的构件的失效模型组成。模型的转移概率矩阵构造过程如下：加入2个吸收状态C和F，分别表示正确输出和失效；修改转移概率矩阵P，将构件i和j之间的原始转移概率Pij修改为RjPij，表示构件i正确执行后控制转移到j的概率；从出口状态n添加有向边到C，转移概率为Rn，表示应用正确执行完成；从构件i添加有向边到状态F，转移概率为(1-Ri)，表示构件失效过程。因此，软件应用的组合模型为由转移概率矩阵ˆP定义的DTMC。应用的可靠度为到达该DTMC吸收状态C的概率。设Q为删除吸收状态C和F所对应的行列后得到的矩阵。表示经过k步转移从初始状态1到达终止状态n的概率。从初始状态1到终止状态n的转移步数k可以取0到无穷大之间的任何值。定义变量S为

因此得到整个软件系统的可靠性为

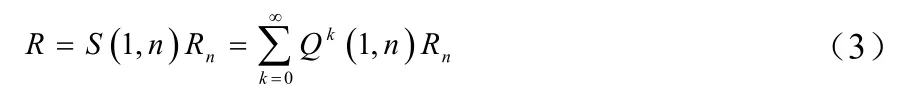
下面将基于路径的模型与DTMC-1相比较。Shooman[12]提出最早的基于路径的模型。它与基于状态的模型的区别在于将软件的体系结构模型和构件的失效模型结合的方法不同，即求解方法不同，基于路径的方法中，体系结构模型假设已知系统所有的执行路径以及每条路径的执行概率失效模型为构件可靠度Ri或路径可靠度采用基于路径的方法得到系统的可靠度为：

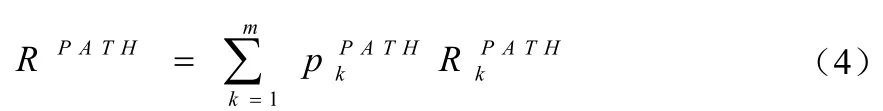
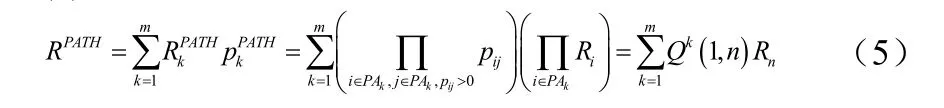
公式(3)中，0k＜＜∞，模型DTMC-1考虑了无数条路径存在的情况。而基于路径的模型，当系统中存在的路径数目有限时，模型可以得到可靠性估计的准确值，此时当系统中存在环路而有无数条路径时，基于路径的方法只能得到可靠性估计的近似值，此时，这是基于路径方法的主要缺点。至此，我们已经完成将基于路径的模型统一到基于体系结构的软件可靠性模型的统一框架中。

2.2 持续运行的软件应用

对于持续运行的软件应用，可靠性度量为软件在稳定运行状态下的可靠性，存在3种形式：软件应用的可靠度，常量失效率，依赖于时间的失效强度。持续运行的软件应用的体系结构可建模为不可约的Markov模型。当每次访问构件的时间满足指数分布时，用 CTMC建模，否则用 SMP或DTMC建模。假设构件失效速率远远小于构件之间的转移速率，因此失效发生前系统能够运行达到一个稳定状态。对体系结构模型求解可以得到每个构件的稳态概率πi。πi表示连续运行的软件应用执行过程中构件的使用情况，表示无失效发生时应用在状态i的平均执行时间比例。对于硬件系统来说，πi=1。当使用不同的构件失效模型时，得到相应的应用可靠性模型不同，如表4所示。

表4 持续运行的软件应用的可靠性分析

表4中的模型DTMC-8，CTMC-8，SMP-12，在目前的基于体系结构的软件可靠性分析的文献中还没有出现过。现存的基于状态的模型得到的应用可靠性度量是软件结构的函数，是一个单一的估计值，而不是一系列随时间变化的预测值，有两种形式：软件应用的可靠度和常量失效率。基于状态的模型的这种“定常”特性无法解决软件测试过程中的故障排除问题。模型 DTMC-8，CTMC-8，SMP-12解决了这个问题，它们得到的可靠性度量是时间依赖的失效强度。它们建立了应用的软件可靠性增长模型，提高了可靠性预测的准确度。这3种模型就是在统一可加模型过程中对可加模型进行改进的结果。

目前提出的可加模型包括两种：Xie模型[13] 和Everett模型[14] 。可加模型考虑的是软件测试阶段，假设每个构件的失效过程可建模为非齐次泊松过程（non-homogeneous Poisson process, NHPP）。如果构件失效过程为NHPP，那么整个系统的失效过程也为NHPP，系统失效强度函数和累计失效数目为每个构件相应函数的总和，即

公式(6)，(7)为Xie模型的表示。Xie模型中为了考虑不同构件加入系统的时间，对每个构件失效模型中相应的函数时间进行调整。Xie模型没有考虑软件体系结构，也就是没有考虑应用执行过程中每个构件的使用情况。

Everett模型，如公式(8)，(9)所示，其中ti表示应用执行过程中构件i的累积执行时间。Everett模型在Xie模型的基础上有所改进，它包含了关于每个构件的相对工作负载信息作为模型参数。它使用测试过程中得到的每个构件累计执行时间来计算构件的累计失效数目和失效强度函数。因此，这个模型考虑了软件构件的使用情况但没有实现建模，也就是隐式地考虑了软件的体系结构。

与现有的模型不同的是，可加模型得到的可靠性度量是时间依赖的失效强度，是时间域的函数，而不仅仅是一个单一的估计值。可加模型是基于体系结构的软件可靠性分析领域中的创新性尝试。它们第一次尝试将已经研究成熟的软件可靠性增长模型应用于基于体系结构的软件可靠性分析中。但是可加模型没有实现黑盒模型和白盒模型（指基于状态和基于路径的模型）的真正结合，因为它们没有实现对软件体系结构的建模。

基于状态的模型中体系结构模型的求解结果πi表示无失效发生时构件i的平均执行时间比例。基于πi，Everett模型中的ti可以表示为ti=πit。这样公式（8）和（9）可转换为

改进后的可加模型的系统失效强度函数和累计失效数目函数。在基于状态的模型的基础上实现了对可加模型的改进，同时完成了体系结构模型的框架对可加模型的统一。

3 举例说明

本节对第三节介绍的基于体系结构的软件可靠性模型的统一框架进行举例说明。使用文献[10] 中介绍的应用作为本节的运行实例。该应用提供一个面向语言的用户界面，允许用户来描述天线阵列的配置。目的是给定用适当阵列定义语言描述的天线阵列配置，生成满足预定义的格式和用户特征的一个数据文件。该应用是为欧洲航天局开发，分为三个构件：Parser，Computational，Formatting。通过对源代码分析得到应用的体系结构如图1所示。构件E表示应用的终止状态。构件之间的转移概率如表5所示。通过故障注入测试估计每个构件的可靠性，用UNIX实用时钟测量每次访问每个构件时执行时间的期望值ti，结果如表6所示。CTMC模型中离开状态i的速率ui可以通过ti来计算，即

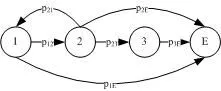
图1 吸收DTMC体系结构模型

表5 构件之间转移概率

为了说明构件失效行为建模为常量失效率的模型，利用构件可靠度Ri和每次访问构件i时执行时间的期望值ti，根据如下公式，计算构件的常量失效率iλ为

根据公式(13)计算得出的构件1，2，3的常量失效率如表6所示。

表6 构件失效行为和期望执行时间

为了说明构件失效行为建模为时间依赖失效强度的模型，假设用G-O模型[15] 建模每个构件的

可靠性增长过程，失效强度表示为 ：

上式中ai表示无限长时间内从构件i检测到故障数的期望值，bi表示每个故障的失效发生率。为了对这两个参数进行估计，在构件 1和 2中分别重新插入两个故障，构件 3无故障。这样a1和a2的值为 2，a3的值为 0。基于ai和ti利用如下公式计算

根据公式(15)得到构件1，2的bi分别为0.0045，0.0146，b3为0。构件失效强度函数如表6。

首先讨论终止应用。应用的体系结构建模为吸收DTMC，如图1所示。采用等级分析方法，当构件失效模型为可靠度时，即DTMC-2，得到应用的可靠度为0.6740；当构件失效模型为常量失效率时，即DTMC-3，得到应用的可靠度为0.6740；当构件失效模型为时间依赖的失效强度时，即DTMC-4，得到应用的可靠度为0.6740。采用组合分析方法，当构件失效模型为可靠度时，即DTMC-1，它的组合模型如图2所示，计算得到的应用的可靠度为0.6874。以上计算结果是通过MATLAB计算得到的。

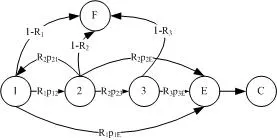
图2 模型DTMC-1的组合模型

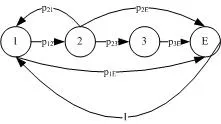
图3 不可约的DTMC体系结构模型

为了说明连续运行的软件应用，增加从状态E到状态1的转移，转移概率连续运行的应用体系结构模型建模为不可约的 DTMC，如图 3所示。采用等级分析方法，当构件失效模型为可靠度时，即DTMC-6，得到应用的可靠度为0.8966；当构件失效模型为常量失效率时，即DTMC-7，得到应用的常量失效率为0.0110；当构件失效模型为时间依赖的失效强度时，即DTMC-8，得到应用的时间依赖的失效强度为

连续运行的应用的体系结构模型建模为不可约的CTMC，如图4所示。设转移速率uE为100/msec。采用等级分析方法，当构件失效模型为可靠度时，即CTMC-5，得到应用的可靠度为 0.9011；当构件失效模型为常量失效率时，即CTMC-7，得到应用的常量失效率为0.0078；当构件失效模型为时间依赖的失效强度时，即CTMC-8，得到应用的时间依赖的失效强度为

图4 不可约的CTMC体系结构模型

4 结论

本文提出了基于体系结构的软件可靠性模型的统一框架。框架以基于状态的模型为核心，通过与基于路径的模型和可加模型进行比较，将这两类模型结合进框架中，实现了所有基于体系结构的模型的统一。我们也详细讨论了框架中每类模型的输入参数和输出，以及如何在软件生命周期中的不同阶段对模型进行选取。

统一框架的建立系统化了当前提出的所有基于体系结构的软件可靠性模型，是对目前基于体系结构的软件可靠性分析研究工作的阶段性总结，并在此基础上进行了延伸。它有利于今后基于体系结构的软件可靠性研究工作有针对性地进一步展开，拉近了可靠性模型研究与用户实际应用之间的距离。

[1] Hamlet D. “Are we testing for true reliability?,” IEEE Software, vol. 13, no. 4, pp. 21–27, July 1992.

[2] Horgan J R and Mathur A P, “Software testing and reliability,” in Handbook of Software Reliability Engineering, M R Lyu, Ed. New York: McGraw-Hill,1996, pp. 531–566.

[3] Goseva-Popstojanova K and K Trivedi S.“Architecturebased approach to reliability assessment of software systems,” Performance Evaluation, vol. 45, no. 2–3, June 2001.

[4] S Gokhale S and Trivedi K S. “Analytical Models for Architecture-Based Software Reliability Prediction: A Unification Framework,” in IEEE Transaction on Reliabiltiy, Vol. 55, No. 4, December 2006, pp. 578-590.

[5] Cheung R C.“A user-oriented software reliability model,”IEEE Trans. Software Engineering, vol. SE-6, no. 2, pp.118–125, March 1980.

[6] Goseva-Popstojanova K,Mathur A P,and Trivedi K S.“Comparison of architecture-based software reliability models,” in Proc. of Intl. Symposium on Software Reliability Engineering, Hong Kong, November 2001.

[7] Gokhale S, Wong W E, Trivedi K S, and Horgan J R. “An analytic approach to architecture-based software reliability prediction,” in Proc. of Intl. Performance and Dependability Symposium (IPDS 98), Durham, NC,September 1998, pp. 13–22.

[8] Laprie J C and Kanoun K.“Software reliability and system reliability,” in Handbook of Software Reliability Engineering, M. R. Lyu, Ed. New York: McGraw-Hill,1996, pp. 27–69.

[9] Ledoux J and Rubino G. “A counting model for software reliability analysis,” IASTED Journal on Simulation,1997.

[10] Littlewood B. “Software reliability model for modular program structure”, IEEE Transaction on Reliability, 28(3)(1979):241～246.

[11] Kubat P, “Assessing reliability of modular software,”Operations Research Letters, vol. 8, no. 35–41, 1989.

[12] Shooman M L. “Structural models for software reliability prediction,” in Proc. 2nd Int’l Conf. Software Engineering,San Francisco, CA, October 1976, pp. 268–280.

[13] Xie M and Wohlin C. “An additive reliability model for the analysis of modular software failure data,” in Proc.Sixth Intl. Symposium on Software Reliability Engineering, Tolouse, France, October 1995, pp. 188–193.

[14] Everett W.Software component reliability analysis, in:Proceedings of the Symposium on Application-specific systems and software Engineering Technology(ASSET’99), 1999, pp: 204～211.

[15] Goel A L and Okumoto K. “Time-dependent errordetection rate models for software reliability and other performance measures,” IEEE Trans. Reliability, vol. R-28,no. 3, pp. 206–211, August 1979.