基于小波变换的分类矢量量化编码
郑秋梅,闵利田
0 引言
小波分析[1-2]是一种信号的时间-尺度(时间-频率)分析方法,它具有多分辨分析的特点,而且在时频两域都具有表征信号局部特征的能力,是一种窗口大小固定不变但其形状可以改变的时频局部化分析方法。有效的克服了傅立叶变换在处理非平稳的复杂图像信号时所存在的局限性。因而被广泛应用于图像处理领域。迄今为止,人们已经提出了许多基于小波的图象压缩方法,如基于小波的零树编码方法,基于小波的分形编码方法,基于小波的矢量量化方法等等。根据香农率失真理论,矢量量化比标量量化(矢量量化是标量量化的扩展)效果好。只要码矢数足够大, 码矢维数足够高,则矢量的量化误差能够得到香农所规定的下限。研究表明,利用小波变化和矢量量化相结合的方法,能够取得较好的压缩效果。
本文提出了一种新的高压缩比图像压缩算法,结合小波变换和矢量量化的优点,图像经过3级小波变换后,同方向各级子带的小波系数按照四叉树规则构成矢量,然后按照矢量的能量进行分类矢量量化,该方法的矢量组成充分考虑了小波系数带内以及带间的相关性,采用分类矢量量化,可以对不同方向的矢量采用不同的量化策略,可以大大减少编码比特。
1 算法原理
1.1 小波变换
小波是由一个函数 )(xψ经伸缩和平移得到的一组函数
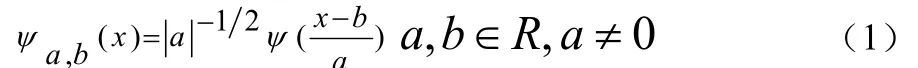
其中(x)ψ就称为基本小波或母小波,它满足相容条件:
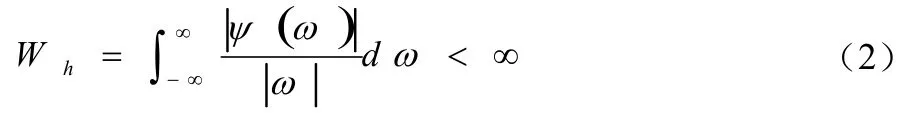
其中(ωψ是)(x)ψ的傅立叶变换。对于任意的函数或者信号其小波变换定义为:

对于连续小波变换,可通过对其尺度参数a和平移参数b的采样而离散化,从而形成离散小波变换。
S.Mallat于1988 年提出了小波多分辨分析算法,十分适合于分析图像。1989年,Daubechies用基于离散滤波器迭代的方法构造了紧支集的规范正交小波基,从而使小波分析广泛用于图像分析,而且从理论上证明,正交小波分解后的信号可以精确地恢复原始信号。
根据小波变换理论,一幅图像经过若干级小波分解后,可得到一系列不同方向(分辨率)的多种子带(子图像),而且这些子带具有4个特点:[3]
(1) 不同方向的子带对应的频率不同;
(2) 图像的能量主要集中在低频子带,高频子带所占的能量很少;
(3) 相同方向不同尺度子带之间具有相关性(纵向相关);
(4) 不同方向不同尺度子带也具有相关性(横向相关) ,即图像能量在不同方向、不同尺度高频子带中的分布非常相似,接近Gamma或Laplacian分布。
小波分析是一种信号的时间-尺度(时间-频率)分析方法,它具有多分辨分析的特点。即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,很适合于探测正常信号中夹带的瞬变反常信号并分析其成分。图像经过小波变换以后的系数在不同方向都呈现出各种相关特性,在进行图像处理的时候可以充分的利用这些相关特性,能够取得较好的效果。
1.2 矢量的构成

图1 图像3级小波分解示意图
图像经小波分解后的系数存在的各种相关性,如同方向不同子带之间的零树性,同一子带中相邻系数之间的相关性等,如果能充分的考虑小波系数的各种相关性,就能够得到较高的压缩效率。
常见的矢量构成方式有:(1) 在每一个子带根据不同的码率分配和失真度分别在不同子带形成不同维数的矢量。(2)跨带矢量构成。这两种方法只是单独得利用了小波系数各种相关性中的一种,对小波系数的相关性没有充分利用。本文的矢量构成充分考虑了同一子带和同方向不同子带中小波系数的相关性,可以取得较高的压缩比。具体组成方式如下:
如图1所示,构造矢量时,第三级各子带(HH3、HL3和LH3)矢量大小为2×2;第二级各子带(HH2、HL2和LH2) 矢量大小为4×4;第一级各子带矢量大小为8×8。其中第二级子带中的系数为第三级子带系数的子节点,第一级子带中的系数为第二级子带系数的子节点,这样总共构成一个84维的矢量[4]。
与文献[5] 构成矢量的方法相比较,本文方法充分考虑了小波系数的各种相关性,能够取得较高的压缩比。但是由于矢量维数的提高,也导致算法运行时间过慢。因此可以考虑利用非线性插值方法对矢量进行降维,以提高算法效率。
1.3 分类矢量量化
由于图像复杂多样,形成的矢量也变化多端,因此要建立一个囊括各种变化的码书不太可能,于是就出现了分类矢量量化,利用分类矢量量化可以对重要的矢量分配较大的码书,对不重要的码书分配较小的码书,这样就可以在保证一定峰值信噪比的情况下,获得较高的压缩比。
本文采用的分类策略如下:首先将矢量分为3类:水平方向,垂直方向和对角方向。对于不同方向的矢量可以采用不同的码书尺寸进行量化。然后对各方向的矢量按照能量进行分类,设矢量维数为K,矢量能量可表示为

相对于一定的能量门限T,若W>T则为重要矢量,否则则为非重要矢量,对于重要矢量对恢复图像的质量影响很大可以分配较大码书,对于非重要矢量可以分配较小的码书[5] 。
与文献[4] 的方法对比,利用分类矢量量化以后,可以对不重要的矢量分配较小的码书,可以进一步的提高压缩比,同时码书变小,还可以提高算法的时间效率。
1.4 非线性插值方法
在矢量量化中,一般希望矢量维数很大,这样不但可以提高算法的压缩比而且随着矢量维数的增大,量化器的性能也会提高。但是对于给定的比特率,矢量量化的复杂度与矢量的维数呈指数规律递增。本文提取84维矢量进行矢量量化,矢量维数较高,增加了矢量量化的复杂度。因此可以考虑使用非线性插值方法来降低矢量维数,同时起到降低算法复杂度的效果。

图2 非线性插值矢量量化图
如图 2所示,量化器存在两个码书,其中编码码书C的维数要小于解码码书C*的维数,k维特征矢量u是从n维矢量x中抽取出来的,即u=g(x),其中k<n。矢量u经过编码码书C进行编码,找出C中与u最近的码矢,输出标号i,最后,通过解码器在解码码书中搜索对应于标号i的码矢X',把X'作为x的量化估计。
假设训练矢量集Γ包含M个训练矢量xj,满足训练率M/N>>1。对这些n维训练矢量进行特征提取,形成k维特征矢量集。用LBG算法对这些特征矢量集进行训练,可生成大小为N的码书C。利用码书C可将特征矢量集划分为N个胞腔,相应得将训练矢量集也分成了N个胞腔,即
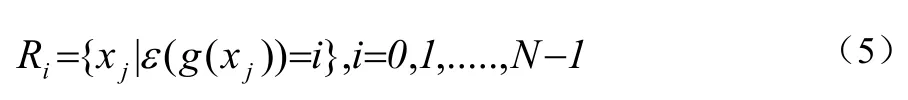
从而码书C*的第i个码字ci可由下式计算:

本文在对矢量进行分类矢量量化时,对水平,垂直和对角 3个方向的矢量应用非线性插值方法,我们取矢量的前20个分量构成特征矢量,采用LBG算法训练产生20维的编码码书C,再由(6)式生成84维的解码码书C*。
1.5 最低频子带的处理
由于最低频子带含有图像的大部分能量,为了保证恢复图像的质量,可以对该子带单独使用Huffman编码进行压缩。这样可进一步提高压缩图像的压缩比。
1.6 算法流程
本文算法的步骤可概括如下:
(1) 对图像进行3级小波分解,对小波分解后的系数按照本文算法提取矢量。
(2) 对提取得矢量按照能量进行分类,对重要矢量和非重要矢量分别编码。
(3) 应用非线性插值矢量量化器进行矢量量化。
(4) 对水平,垂直和对角3个方向量化完毕之后,再对最低频的小波系数单独进行Huffman编码。
2 实验结果及分析
本文利用256个灰度等级(即8位量化)的512×512标准Lena图像进行实验,选取haar小波对图像进行3级小波分解,这主要是因为haar小波能同时满足正交和对称性[7]。
对小波分解后的系数,按照本文算法组成矢量。表1列出了3个方向的平均能量。按照平均能量进行分类,利用LBG进行训练生成不同尺寸的码书。对重要类矢量水平,对角和垂直3个方向的码书长度取256,256和256,对非重要类矢量3个方向的码书长度分别取128,128和128。实验结果如表2所示。

表2 不同策略性能对比
试验结果表明,本文算法在保证一定的PSNR值得情况下,获得了较高的压缩比。非线性插值方法的引入也使算法的运行时间相对于文献[4]大幅度缩减。同时由于采用分类矢量量化,还可以根据不同的能量门限获得不同的压缩效率,能量门限越低,重要类矢量的个数越少,可以获得更低的编码率,实验表明最低可达到0.048,此时所有矢量都被认为是非重要的矢量。但是相应的峰值信噪比也会降低。

图3
4 结束语
本文提出了一种新的矢量组成方式和分类矢量量化结合的方法,借助零数思想组成一个84维矢量,然后对矢量进行相应的分类,分为水平,垂直和对角3个方向。然后根据矢量的能量进行重要度分类,对重要类矢量分配大的码书,对非重要类矢量分配较小的码书,同时结合非线性插值方法进行矢量量化。试验结果表明,本算法能够在保证较高峰值信噪比的情况下,获得较低的编码率,取得了令人满意的结果。但是由于提取得矢量维数较大,虽然使用了非线性插值方法进行了相应处理,相对于20维左右的矢量提取算法,本算法运行时间还是比较慢。而且使用非线性插值方法也增加了额外的开销。因此本算法比较适用于对图像质量要求不高,而又希望图像压缩比比较高的情况。
[1] Mallat S. Multifrequency channel decomposition of images and wavelet models[J] . IEEE Trans on ASSP,1989,37(12):2091-2110.
[2] Atonini M, Barlaud M, Mathieu P. Image coding using wavelet transform[J] . IEEE Trans on Image Processing,1992,1(2):205-220.
[3] 张兆礼,赵春晖,梅晓丹. 现代图像处理技术[M] . 北京:人民邮电出版社,2002:295-296.
[4] 王茂芝,徐文皙,佘春东. 一种高效的小波变换跨带矢量量化编码[J] . 计算机应用,2004,24:379-381.
[5] 郑勇,李德明,朱维乐. 采用方向树结构矢量组合的小波图像分类矢量量化[J] . 电子信息学报,2004,27(12):1959-1963.
[6] 孙圣和,陆哲明. 矢量量化技术及应用[M] . 北京:科学出版社,2002:104-105.
[7] 马杜祥,刘贵忠等. 基于小波变换的图像和视频压缩编码[J] . 工程数学学报,2001,18(5):17-30.

