水泥搅拌桩重力式挡土墙变形的有限元分析

□文/赵晓萍 高 翔

基坑开挖过程中对围护结构的变形预测与控制十分重要，有限元理论的发展为解决这一问题提供了有效途径。本文以实际工程为背景，利用有限元理论分析水泥搅拌桩重力式挡土墙在不同开挖深度、嵌入深度及加固宽度下的变形情况，研究重力式围护结构的变形规律。

有限元模型的计算

基本假定及建模思想

（1）模型中的介质均为连续性介质。

（2）考虑土体的非线性特点，有限元模拟中将土体本构关系定为弹塑性本构DP-model模型关系。

（3）在模拟基坑开挖过程中，将开挖部分单元用“生死单元”代替，通过“杀死”不同深度的单元来模拟土体分步开挖过程，从而了解分步开挖时间对变形及内力的影响，进而验证“时空效应”原理的正确性。

基坑模型简图及有限元模型建立

工程为10栋建筑物组成的综合服务基地，占地面积约为50 000 m2。计算的为9号楼基坑，该楼建筑面积为73 m×81 m，地上8层，地下1层用作停车库。基坑大部分开挖深度5.4 m，局部集水坑开挖深度达到6.2 m。

由于基坑在尺寸、开挖深度、空间位置上具有对称性，为简化计算、加快计算速度，取基坑的1/2模型进行计算，见图1。

根据以往工程经验及有限元计算结果，基坑开挖影响宽度约为基坑开挖深度的3～4倍，影响深度约为基坑开挖深度的2～4倍。为了减少模型计算的“边界的约束效应”，模型中将水平影响宽度和竖向影响深度都取为4倍的基坑开挖深度，即有限元模型的计算范围取值为L(模型的长度)×B(模型的宽度)＝62.3 m×29.2 m。

基坑有限元模型共划分2 536个单元和3 984个节点。位移边界条件为两个侧面x方向的位移施加约束，y方向位移自由；上表面x、y方向位移均自由；模型底面考虑已超过影响深度范围，可以近似认为不动，故x、y方向均施加约束。

模型参数取值

（1）土体本构关系为Dr ucker-Pr ager-model。自上而下土层的参数根据地质勘察报告进行取值，见表1。

数值模拟结果分析

不同开挖深度

为研究分步开挖过程中围护结构体系自身及临近土体的应力及位移变化趋势，在有限元中通过“生死单元”技术模拟基坑分步开挖过程，本文分别选取两种开挖深度H＝2.5 m和H＝5.4 m。

图2为开挖深度2.5 m时的水平位移、竖向位移云图，通过云图的分布规律可以清楚地获知基坑分步开挖过程中位移、应力及塑性应变的分布和变化规律。图2中不同颜色代表不同的数值，红色表示大值，蓝色表示小值。

图2 开挖深度2.5 m时的位移云图

图3为开挖深度分别为2.5 m和5.4 m时水泥搅拌桩重力式挡土墙水平位移曲线。

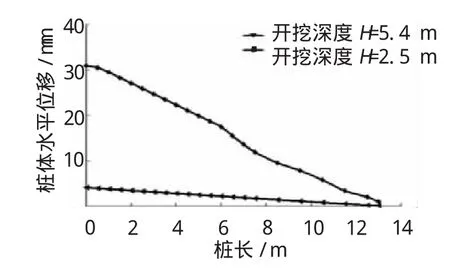
图3 水泥土搅拌桩水平位移

从图3可以看出，当开挖深度为2.5 m时，桩体的最大水平位移值为4.01 mm，而当开挖深度达5.4 m时，桩体最大水平位移值为30.91 mm；即当基坑开挖深度仅增加2.9 m时，桩体最大水平位移却增加了6.7倍，增长的幅度很大。表明基坑开挖深度在时间及空间上存在一个临界值，即当开挖深度超过某一深度之前，桩体及临近土体的变形很小，但超过这一深度后，桩体水平位移变化相当迅速，这一过程发生的时间也比上一过程发生的时间要短。

图4和图5分别为不同开挖深度下临近地表沉降曲线和坑底隆起曲线。

图4 临近地表沉降位移曲线

图5 不同开挖深度下坑底隆起曲线

从图4和图5可以看出，曲线的变化形状和规律均表现出在开挖的初期地表沉降及坑底隆起值较小，随着开挖深度的增加及时间的增加，到某一临界值后，地表沉降及坑底隆起量大幅度增加，变化非常迅速。

基坑开挖过程中桩体水平位移、临近地表沉降及坑底隆起数值模拟结果和理论研究与众多实测结果的变形规律和趋势非常一致，3种变形在时间和空间分布上所具有的特殊规律很好地验证了“时空效应”原理的存在性和正确性。

不同加固深度

为研究水泥土搅拌桩重力式挡土墙不同加固深度下围护结构体系自身及临近土体的应力及位移变化趋势，选取设计桩长为13 m和16 m，同时考虑分步开挖的影响，设计开挖深度分别为H=2.5 m和H=5.4 m的情况。图6为不同加固深度下水泥搅拌桩重力式挡土墙水平位移曲线。

图6 不同加固深度下桩体水平位移

从图6可以看出，当开挖深度为2.5 m，桩长L为13 m和16 m两种情况下桩身水平位移基本上没有太大变化，水平位移最大值也较为接近，表明桩长增加3 m对桩身的水平位移基本上没有影响，从另一个角度说明13 m的桩长对开挖深度仅为2.5 m的基坑不管是从围护结构安全还是从变形角度考虑都已经是满足要求的，继续增加桩长并不能起到限制变形的效果，反而造成浪费；开挖深度达到5.4 m时也说明了这一现象，桩长L=16 m时的最大水平位移值仅比桩长L=13 m时的最大水平位移值小2 mm左右，增加桩长并不能很有效地抑制桩身的水平位移。

图7和图8分别为不同加固深度下临近地表沉降曲线和坑底隆起曲线。

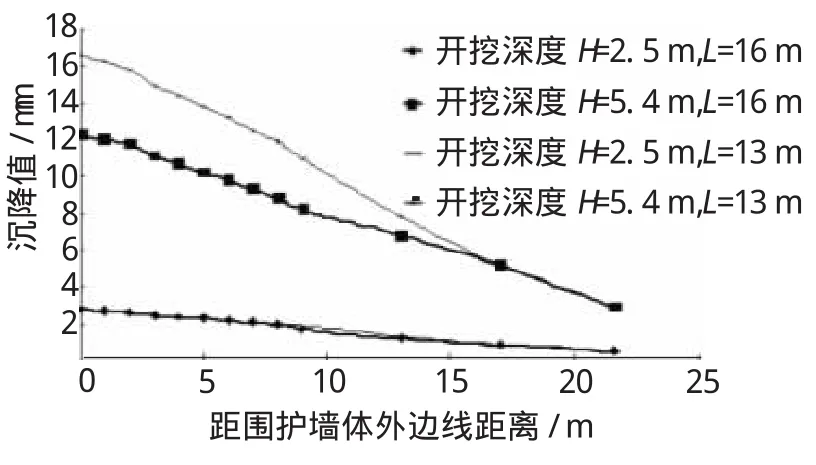
图7 不同加固深度下临近地表沉降

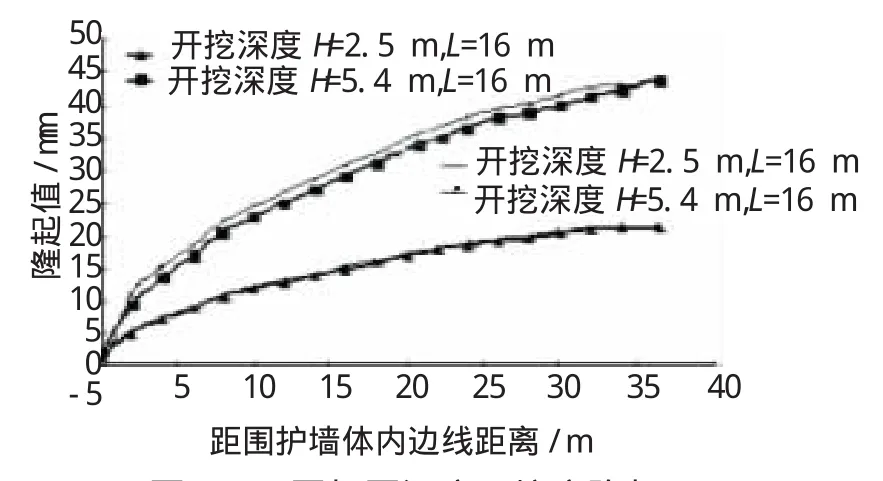
图8 不同加固深度下坑底隆起

从图7和图8可以看出，在开挖深度为2.5 m时，桩长增加3 m对临近地表沉降及坑底隆起基本没有影响，地表沉降及坑底隆起最大值基本相同，这一变化规律与水平位移变化规律一致；当开挖深度达到5.4 m时，桩长增加3 m对临近地表的沉降有一些影响，沉降最大值减少约4.1 mm，对坑底隆起仍然没有太大影响，隆起最大值约增加0.8 mm。

综上分析，欲通过增加水泥搅拌桩桩长来减少围护结构自身的水平位移、邻近地表沉降及坑底隆起效果不是很明显。一般来说，水泥搅拌桩重力式挡土墙的嵌入深度为开挖深度的0.8～1.2倍，在嵌入深度满足计算要求后，一味地增加桩长用以限制和减少变形效果不明显，反而会造成严重浪费。

不同加固宽度

为研究水泥搅拌桩重力式挡土墙不同加固宽度下围护结构体系自身及临近土体的应力及位移变化趋势，选取设计加固宽度为4.2 m和5.7 m，同时考虑分步开挖的影响，设计开挖深度分别为H=2.5 m和H=5.4 m的情况。图9为不同加固深度时水泥搅拌重力式挡土墙水平位移曲线，为了与原设计加固宽度进行对比，将加固宽度为4.2 m的桩身水平位移绘制在同一张图中。

图9 不同加固宽度下桩体水平位移

从图9可以看出，当开挖深度为2.5 m，加固宽度为4.2 m和5.7 m两种情况下桩身水平位移变化较大，当开挖深度为2.5 m时，加固宽度增加1.5 m后，水平位移有所减小，但减小的幅度并不是十分明显；当开挖深度达到5.4 m时上述这一规律非常明显；加固宽度为4.2 m时的桩顶最大水平位移值为31 mm，约为加固宽度5.7 m时桩顶最大水平位移值10.2 mm的3倍，表明加固宽度增加1.5 m对桩身的水平位移的影响非常显著，即对桩身水平位移的限制效果非常好。从另一个角度说明尽管4.2 m厚的重力式挡土墙已经能够满足强度及变形的要求，但如果能够继续加大重力式挡土墙的加固宽度将会很高效地限制桩身水平变形的发展。

图10和图11分别为不同加固宽度下临近地表沉降曲线和坑底隆起曲线，曲线的变化形状和在时间及空间分布上的变化规律与前面的分析基本相同。

图10 不同加固宽度下临近地表沉降

图11 不同加固宽度下坑底隆起

从图10和图11可以看出，在开挖深度为2.5 m时，挡土墙加固宽度增加1.5 m对临近地表沉降及坑底隆起有所影响，但影响不是太明显，这一变化规律与前面水平位移变化规律基本一致；当开挖深度达到5.4 m时，挡土墙加固宽度增加1.5 m对临近地表的沉降影响相当明显，沉降最大值减少约11 mm，竖向沉降得到了较为显著地限制，对坑底隆起的限制不是十分明显，隆起最大值约增加1.5 mm。

综上分析，欲通过增加水泥搅拌桩重力式挡土墙加固宽度来减少围护结构自身的水平位移、邻近地表沉降效果十分明显。一般来说，水泥搅拌桩重力式挡土墙的加固宽度为开挖深度的0.7～0.8倍，在基坑周边环境较为复杂的情况下，通过合适地加大加固宽度能够较为有效地限制和减少围护结构自身、临近地表变形，但对坑底土体隆起变形的抑制效果不是很明显。

结论

（1）本文通过有限元ANSYS程序建立数值模型对水泥搅拌桩重力式挡土墙围护结构的3种变形进行了模拟并考虑了不同墙宽、墙深及分步开挖等情况下围护结构水平变形、坑底隆起和地表沉降的变化趋势及规律，模拟结果表明有限元模拟水泥搅拌桩重力式挡土墙的变形规律是可行、有效的。3种变形在时间和空间分布上所具有的特殊规律很好地验证了“时空效应”原理的存在性和正确性。

（2）基坑开挖深度在时间及空间上存在一个临界值，即当开挖深度超过某一深度之前，桩体及临近土体的变形相当小，但超过这一深度后，桩体水平位移变化相当迅速，这一过程发生的时间也比上一过程发生的时间要短，即超过某一临界，变形迅速完成，因此在工程实践中，要尽量减少基坑无支撑的暴露时间。

（3）通过增加水泥搅拌桩重力式挡土墙嵌入深度，即增加桩长来减少围护结构自身的水平位移、邻近地表沉降及坑底隆起效果不是很明显。

（4）通过增加水泥搅拌桩重力式挡土墙加固宽度，来减少围护结构自身的水平位移、邻近地表沉降效果十分明显，但对坑底土体隆起变形的抑制效果不是很明显。