采空区稳定性分析与评价

张 建,张远芳,袁铁柱,陈小强

(新疆农业大学水利与土木工程学院,新疆 乌鲁木齐 830052)

采空区稳定性分析与评价

张 建,张远芳,袁铁柱,陈小强

(新疆农业大学水利与土木工程学院,新疆 乌鲁木齐 830052)

由于经济建设的需要,地下工程越来越多,原有地层结构受到不同程度的干扰,地面塌陷将威胁着广大群众的生命财产安全。该文以力学平衡方法为基础,针对采空区上覆岩体的地层和厚度分布不同,采用不同的力学分析方法进行研究,并以工程实例进行了稳定性分析与评价。提出了以采空区上覆岩体相对应的临界厚度为评价指标的被动侧向压力情况下的力学模型和以抗滑安全系数为评价指标的主动侧向压力情况下的力学模型,这两种公式分别适用于上覆岩层较厚和较薄的两种采空区稳定性评价。实例计算结果与工程实际情况基本一致,说明该方法可以用来分析和评价采空区的稳定性。

采空区;力学平衡;稳定性分析

0 前 言

采空区的稳定问题一直以来都困扰着人们,其给人类的生产生活带来的负面影响甚多。对于采空区稳定性的研究目前应用的较多的主要有经典唯象学方法、力学方法和数值分析方法。经典唯象方法具有代表性的是1954年波兰学者李特维尼申首先提出的开采沉陷的随机介质理论,后由我国学者发展成为概率积分法[1]。力学方法主要有俄罗斯的M.M.普罗托吉亚科夫于1907年提出的拱形冒落论和德国人哈元和吉列策尔于1928年提出的压力拱假说;由德国的舒尔茨和施托克提出的悬臂梁(板)冒落论和冒落岩块碎胀充填论;我国学者发展了冒落岩块铰结论,提出的砌体梁平衡说及采场薄板矿压理论;谢和平院士等提出的矿山岩体损伤力学方法开拓了“矿山岩体力学研究与应用”新研究领域[2]。数值分析法主要有有限元、边界元、离散单元法、拉格朗日元法、非连续变形分析和流形元法等方法[3]。这里通过2种力学模型分析不同受力情况下的采空区上覆岩体稳定性。

1 材料与方法

1.1 材料

由于不同地域和不同矿区,采空区上覆岩体的组成和性质有很大的差异,采空区上部的地层分布也有所不同,针对不同的矿区和不同的上覆岩体的分布情况和力学参数,应采用不同的力学分析方法;这里假设所研究范围内的上覆岩体和表层岩土体均为均质材料。

1.2 研究方法

将采空区上部的表层土体作为均布荷载处理,研究对象为假想滑动破坏面范围以内的隔离岩体,隔离岩体受到上部表层土体的荷载作用、两侧岩土体的侧向力作用及自身重力作用,采用力学平衡方法对隔离岩体进行受力分析,采空区上覆岩体要保持稳定状态,则需要满足相应的力学条件。通过这种稳定状态条件对采空区稳定性进行分析与评价。

2 力学模型的建立

2.1 模型1

假设采空区上覆岩体沿某一破坏面发生破坏,该破坏面与竖直方向成α=45°-φ/2角度[4];矿体倾角为β;H为采空区上覆岩体厚度;b为采空区宽度;h为采矿厚度;γ为采空区上覆岩体平均重度;γ*为表层土平均重度。如图1所示。

取滑动面范围岩体为隔离体,其受力情况为:G为采空区上覆岩体的自重;P为两侧岩土体对采空区上覆滑动范围内岩体的支撑力;q为表层土体的等效均布荷载。

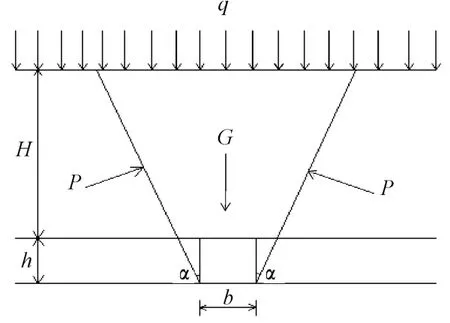
图1 垂直矿井走向剖面

上覆岩体两侧所受支撑力为[4]:

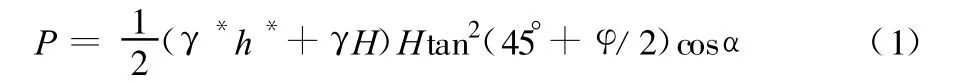
上覆岩体所受自重G为:

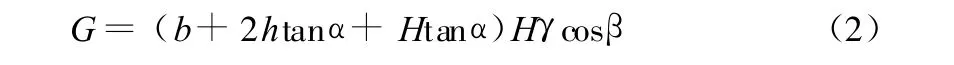
因此,采空区上覆岩体所受合力Q为:

从受力分析可知,当Q=0时,采空区上覆岩体处于极限平衡状态;Q＜0时,采空区上覆岩体处于稳定状态;Q＞0时,采空区上覆岩体处于失稳状态[5,6]。若采空区上覆岩体处于极限平衡状态,则:

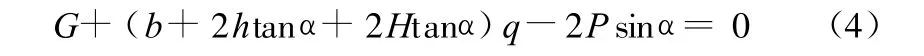
由上式可得当采空区上覆岩体处于极限平衡状态时,采空区上覆岩体相对应的临界厚度H0为:

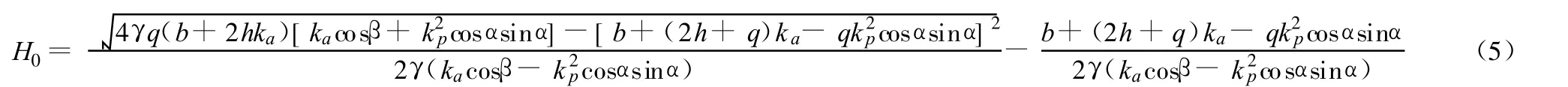
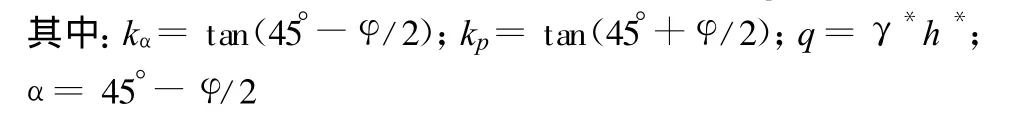
根据《工程地质手册》,考虑一定安全度情况下,当采空区上覆岩体厚度H＜H0时,空洞顶板不稳定;当采空区上覆岩体厚度H0＜H＜1.5H0时,空洞顶板稳定性差;当采空区上覆岩体H＞1.5H0时空洞顶板稳定[7]。

2.2 模型2

假设采空区上覆岩体沿某一破坏面发生破坏,该破坏面与竖直方向成α=45°-φ/2角度[4];矿井倾角为β;H为采空区上覆岩体厚度;b为采空区宽度;h为采矿厚度;γ为采空区上覆岩体平均重度;γ*为表层土平均重度。如图2所示:取滑动面范围岩体为隔离体,其受力情况为:G为采空区上覆岩体自重;P为两侧岩土体对采空区上覆岩体的压力;q为表层土体的等效均布荷载。

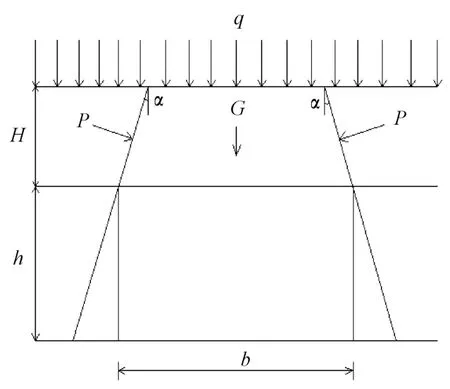
图2 垂直矿井走向剖面

上覆岩体两侧所受压力为[4]:

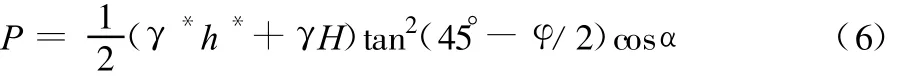
上覆岩体自重G为:

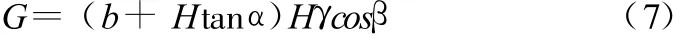
沿破坏面上的摩擦力T为:

因此,采空区上覆岩体所受的合力Q为:

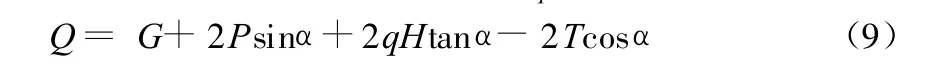
与模型1同样道理,当Q＜0时,采空区上覆岩体处于稳定状态;Q＞0时,采空区上覆岩体处于失稳状态;Q=0时,采空区上覆岩体处于极限平衡状态[5,6]。

对于模型2,从抗滑角度考虑,当破坏面上的滑动力小于抗滑力时,采空区上覆岩体才能处于稳定状态。其滑动力为:

根据《工程地质手册》,抗滑安全系数宜大于1,一般情况取安全系数为1.25为宜[7]。

对比模型1和模型2,模型1适用于上覆岩层较厚的采空区上覆岩体的稳定性分析;模型2适用于上覆岩层较薄的采空区上覆岩体的稳定性分析。

3 计算实例

实例1:某煤矿采空区为倾斜煤层,主要采用单斜井开采,主斜井长约 160 m,该煤矿矿体倾角为35°,埋深约35 m。采煤巷道尺寸为5m×5 m,该煤矿地层情况见表1。

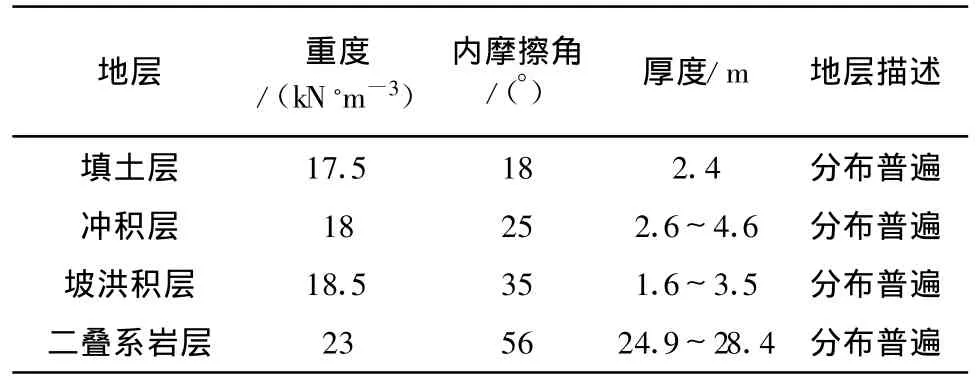
表1 采空区上部地层情况

实例1其埋深在35 m范围,采空区上覆岩体厚度在24.9 m～28.4 m范围内,岩层之上的土层总厚度不大,所以选用模型1进行分析。根据模型1计算结果见表2所示。

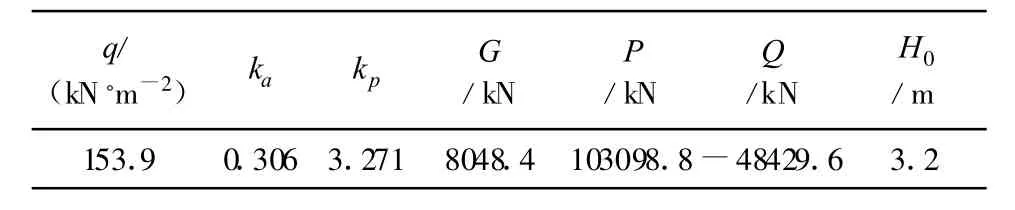
表2 模型1计算结果

实例2:某金矿老采空区为人工开采留下的老矿洞,采金方式多为巷道式开采,矿体倾角约25°,主要采金巷道的大小约1.8 m×2 m,巷道长度不等,最长巷道达150 m左右,平均埋深在8m左右,地层情况见表3。

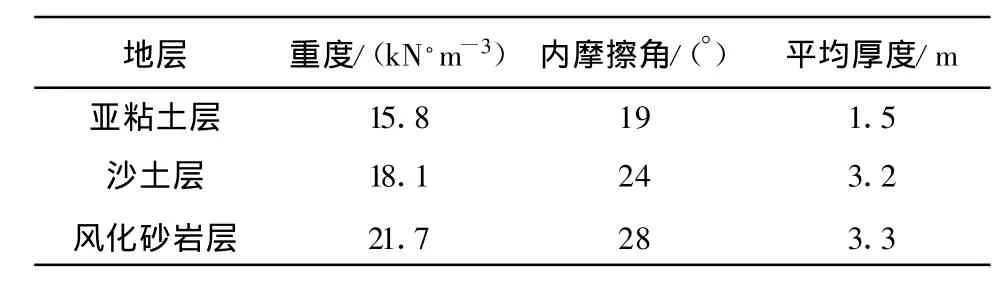
表3 采空区上部地层情况

实例2中该采空区的上覆岩层厚度较小,平均岩层厚度在3.3 m左右,选用模型2进行计算分析,根据模型2计算结果见表4所示。

表4 模型2计算结果

4 结果分析

从计算结果中可以看出,实例 1中的Q＜0,煤矿采空区上覆岩体处于稳定状态,上部覆岩不会产生向下的位移即该采空区的地表无沉降。从临界厚度来看,该煤矿采空区上覆岩体H=(24.9～28.4)m＞1.5H0,根据《工程地质手册》,当采空区上覆岩体H＞1.5H0时空洞顶板稳定[7]。说明该煤矿采空区上覆岩体稳定;实例2中Q＞0,该金矿采空区的上覆岩体处于不稳定状态,上部覆岩将会产生向下的位移即该采空区的地表沉降甚至塌陷;而该采空区的安全系数fs=0.09＜1,所以该采空区不稳定,需要对其进行合理的工程处理。从2个实例所应用的模型来看,分析与评价的结果与工程实际情况基本一致,说明2种模型具有一定的实用性。

5 结 论

针对不同地层情况和受力方式建立了2种力学模型,通过这2种模型对采空区上覆岩体的受力情况进行分析,在2种力学模型下得到了2种受力情况下用来评价采空区稳定性的力学公式。结合2个工程实例运用模型进行了计算,计算结果验证了2种模型的可用性,这2种模型简单且具有实用性,可以用来分析和评价采空区的稳定性。

[1]姜岩,田茂义.矿山开采地表下沉与变形预计新方法[J].矿山压力与顶板管理,2003,(3):64-67.

[2]贾喜荣.矿山岩层力学[M].北京.煤炭工业出版社,1997:265-268.

[3]何满潮.矿山开采中的岩土工程技术新进展[C]//全国岩土与工程学术大会论文集.北京:人民交通出版社,2003:125-128.

[4]吴德伦,黄质宏,赵明阶.岩石力学[M].重庆.重庆大学出版社,2002:276-277.

[5]高晓辉,彭建兵,杨天亮,等.西合高速公路采空区稳定性评价及其治理方案[J].地球与环境,2005,33(3):139-141.

[6]郭广礼,何国清,催曙光.部分开采老采空区覆岩稳定性分析[J].矿山压力与顶板管理,2003,(3):70-73.

[7]工程地质手册第四版[M].北京:中国建筑工业出版社,2006:1598-1599.

Analysis and Appraisal for Stabiliy of Goaf

ZHANG Jian,ZHANG Yuan-fang,YUAN Tie-zhu,CHEN Xiao-qiang
(College of Hydraulic and Civil Engineering,Xinjiang Agricultural University,Ulumuqi,Xinjiang830052,China)

Based on the mechanical balancemethod,the passive lateral model and active lateral model are established according to the different stratum and thickness of the top rock of goaf,and the stability analysis and appraisal for goaf aremadewith different instance.It is showed that the calculated result is in agreement with the actual engineering condition,so the method could be used to analyze and appraise the stability of goaf.

goaf;mechanical balance;stability analysis

TD325.1

A

1672—1144(2010)02—0145—02

2010-01-16

张 建(1983—),男(汉族),安徽凤台人,硕士,研究方向为岩土工程。

张远芳(1963—),女(汉族),新疆乌鲁木齐人,硕士生导师,副教授,研究方向为岩土工程。