基于四种方法的月径流预测研究

李 计,李 毅,严宝文,宋松柏

(西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100)

基于四种方法的月径流预测研究

李 计,李 毅,严宝文,宋松柏

(西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100)

径流预测对于水资源的合理开发利用与统筹配置具有重要意义。根据黄土高原地区渭河支流-北洛河状头水文站和泾河张家山站的月径流资料,运用门限自回归模型、神经网络模型、方差分析外推法以及季节水平模型四种方法对其进行预测,观察模拟效果并比较各自优缺点。对于枯水期月径流,季节水平模型对于两站预测合格率均为100%;方差分析外推法对于状头站和张家山站预测合格率分别为90%,80%;门限自回归模型对于两站的预测合格率均为80%;神经网络模型预测两站汛期月径流合格率均为100%。表明季节水平模型适用于枯季月径流的预测,神经网络模型适宜于汛期月径流预测,并且精度良好。

门限自回归模型;神经网络模型;方差分析外推法;季节水平模型;月径流预测

0 引 言

径流预报作为水文预报的重要组成部分,其在防汛、抗旱、水资源可持续开发利用、国民经济建设和国防等领域都有广泛的应用,经济效益巨大[1]。目前径流预报已从经验公式、集总模型走到分布式模型,并取得丰硕成果[2]。

径流预报是通过建立径流时间序列模型对未来一段时间径流信息的预测。但由于水文循环过程及其空间变化的复杂关系和作用关系的非唯一性,使水文现象具有非线性、时变、不确定性的特点[3],因此,水资源系统可被当成一种混沌系统[4]。水文现象的非线性问题研究是探索水文复杂性最为重要的理论问题。近来,非线性时序的分析获得了迅速的发展并且相继出现了一系列非线性时序模型比如“门限自回归模型”、“双线性模型”、“指数自回归模型”、“状态依赖模型”等。但是在径流预报方面各种模型的适应性以及优缺点对比探讨的比较少。

本文以北洛河状头站和泾河张家山站月径流资料为依据,运用DPS数据处理软件中的门限自回归模型、神经网络模型、方差分析外推法和季节水平模型这几种典型的非线性时间序列模型进行月径流预报研究,探讨其在月径流预测中的可行性以及预报精度,并比较这几种方法各自的优缺点。

1 方法及原理

1.1 门限自回归模型(以下简称TAR模型)

TAR模型是由英籍华人H.Tong博士[5]首创的门限自回归模型的扩展。其基本思路就是依某变量的不同取值范围,采用若干个线性回归模型来描述非线性关系,另外还将微分方程中极限环的概念引入非线性随机系统,有效地描述具有周期规律的过程,而且由于门限的控制作用,保证了模型的稳定性。此外,这类模型还可以作为突变现象的一种描述手段。其一般形式是[6]:

式中:Zt是时间序列;φ(j)0,φ(j)1,…,φ(j)i是第j区间自回归系数;pj为第j区间模型阶数(j=1,2,…,L);ε(j)t是独立随机变量;r1,r2,…,rL-1为门限值;L为门限区间个数;d为门限延迟步数。

DPS系统要求输入参数,首先需要确认用作门限变量的标号,这里只有月径流1个变量,故输入1。其次输入门限变量延迟阶数,即(1)式中的d值,这要根据时间序列的意义输入:对于状头站选用1,张家山站采用2。然后输入所建立的自回归模型最大延迟阶数。系统将在最大延迟阶数的约束下进行寻优分析。这里指定自回归模型最大延迟阶数:对于状头站选用7,张家山站采用2。最后输入因变量的标号。因只有1个变量序列,因此,该值是1。在确认模型输入的参数后,再选择对数据进行自然对数转换。最后系统会给出拟合结果。

1.2 神经网络模型

BP网络属于前向神经网络(本文即采用BP模型),是由输入层、隐层和输出层构成的。BP算法就是Back-Propagation(反向传播)算法的简称。BP神经网络通常有1个输入、1个或多个隐含层和1个输出层组成,含有1个隐含层的BP神经网称为3层BP网[7],任何1个3层 BP网能无限逼近任何连续函数[8,9],因此一般多选用3层BP网来进行江河径流量预测。图1为BP模型结构图:

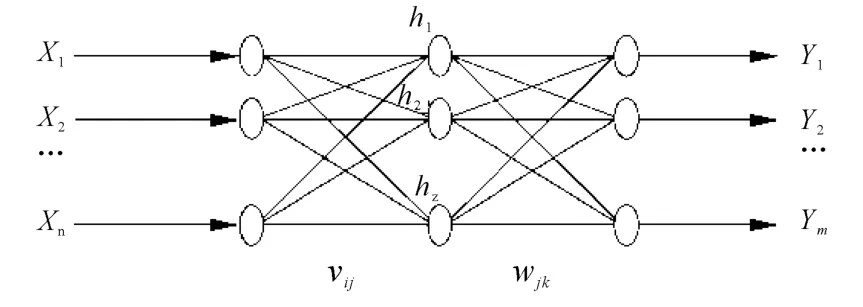
图1 3层BP网络结构图

在反向传播算法应用于前馈多层网络时,采用非对称神经元的非线性作用函数(Sigmoid)激发函数。算法的执行首先对权系数i置初值,然后选择一个输入样本X(Xi-1,Xi-2,Xi-n,1),以及对应的期望输出y;计算各层的输出,求各层的学习误差。

对于输出层有:

修正权值和阈值:

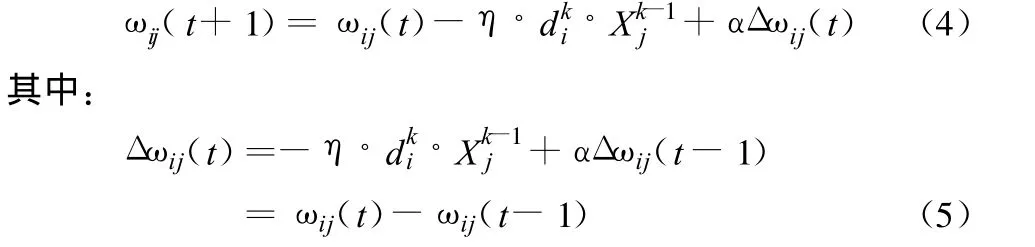
当求出了各个权系数之后,重新对网络输出进行计算,按给定的品质指标判别是否满足要求。如网络已经满足指定要求,则算法结束;否则,返回计算输出,如此循环执行。

进入BP神经网络训练时,按网络的结构确定网络的参数,这里因为只有月径流一个变量,故输入层节点数为1,隐含层1层,最小训练速率取0.1,动态参数0.6,Sigmoid参数为0.9,允许误差0.0001,最大迭代次数1000。数据转换为标准化转换。确定后系统将给出结果。由于实测水文系列往往具有偏态性,因此在模拟前应先消除水文数据的偏态影响,为此应对原始系列进行变换使其偏态减少接近于零。并对输入节点的数值进行标准化转换。

标准化计算:

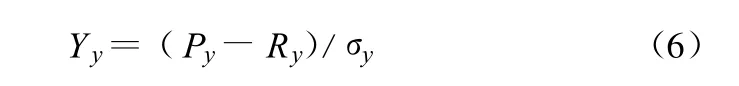
式中:Yy是均值为0、方差为1的标准化量,Ry、σy分别是Py的均值和方差[10]。

1.3 方差分析外推法

方差分析是目前进行水文中长期预报的一种简单常用的有效方法。该方法的原理思路清晰、数学模型简单,其一般形式如下:

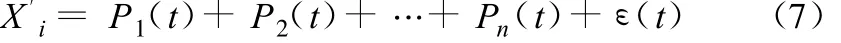
式中:X′i为水文要素序列;Pi(t)为第i个周期序列;ε(t)为随机项。

进行作业预报时,目前常用的做法是取X'i-P1(t)+P2(t)+…+Pn(t),ε(t)项不予以考虑。用DPS系统结束分析过程设置的显著水平Fa=0.05,同时规定原数据序列与相应的周期序列的相关系数必须在0.3以上,否则结束分析过程。

1.4 季节水平模型

考察一个具有季节性变化的时间序列,且各季节周期具有相同的平均值,这时可应用季节性水平预测模型进行预测。显然,月径流序列满足这样的周期性(12个月为一周期)。这种季节性水平模型在第T时段的期望值为:

式中:μ为每时段平均水平;ρT是在时段T的季节比,有ρT≥0,且在一个周期内平均值是1。

2 结果分析

本文采用的月径流数据为泾河张家山站1932年～2006年资料和北洛河状头水文站1937年～2006年月径流资料(其中有些模型本身由于输入数据序列长度受限,故可能选取其中部分年份的资料)。通过DPS数据处理软件中的TAR模型、BP模型、方差分析外推法和季节水平模型对其进行预测,并观测其精度及优缺点(以相对误差不超过30%为合格,月径流单位m3/s)。

2.1 状头站月径流预测

对于TAR模型、方差分析外推法和季节水平模型均采用1937年～2000年月径流资料建立模型;而BP模型采用2000年～2006年资料建模,各模型均采用2001年～2002年数据检验模型。表1分别列出前3种方法模拟效果(本文以1、2、3、11、12 为枯季月径流代表,7、8、9 月份为汛期代表)。

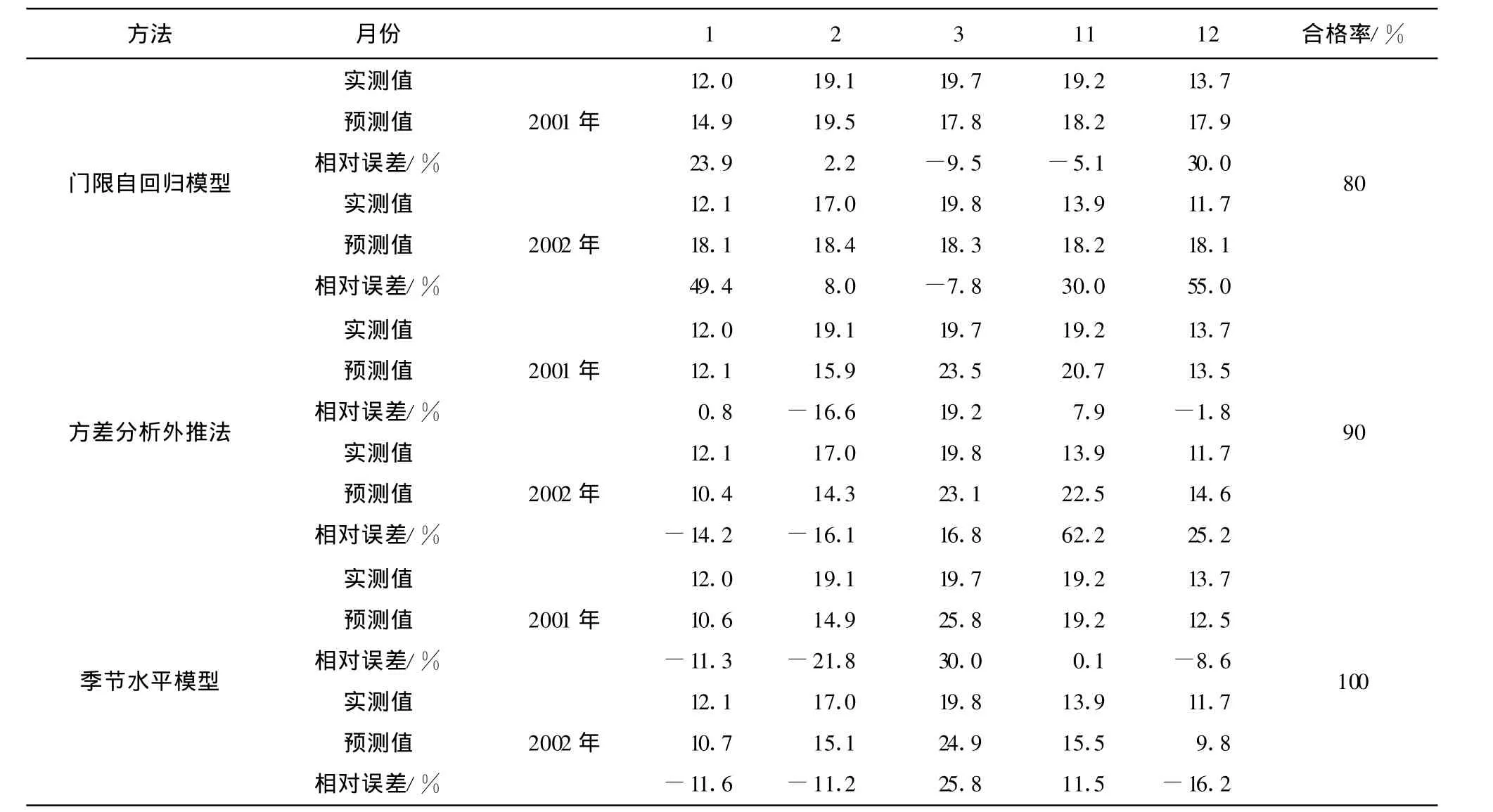
表1 TAR模型、方差分析外推法和季节水平模型的枯季月径流模型预测结果

从表1看出:对于枯季径流的预测,季节水平模型预测效果最好(100%),可作为今后枯季径流预测的较理想的方法。方差分析外推法次之(90%),也可用来预测枯季径流。TAR模型预测效果尚可(80%),可作为参考。

图2给出BP模型预测状头站2001年～2002年月径流效果。

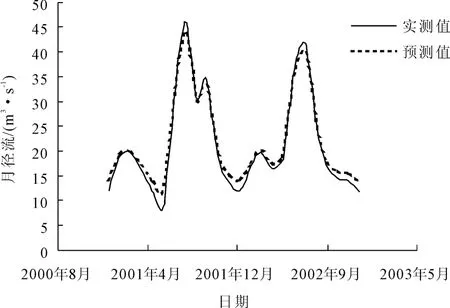
图2 BP模型模拟月径流效果图

从图2看出BP模型的整体模拟效果良好,可以很好的反映月径流序列的变化趋势。尤其是汛期模拟效果较好,可作为汛期月径流预测的一般方法。

表2列出BP模型预测值与实测值对照结果。

表2 BP模型模拟效果

经统计表2用BP模型预测状头站2001年～2002年月径流汛期合格率为100%,全系列预测合格率为92%,预测效果良好。

2.2 张家山站月径流预测

对于TAR模型、方差分析外推法和季节水平模型分别采用1932年～2003年、1977年～2003年、1990年～2003年月径流数据建立模型,2004年月径流资料用以检验模型预测效果。而BP模型采用2000年～2006年资料建模,其中用2004年～2005年数据检验模型。前3种方法的预测效果见表3。

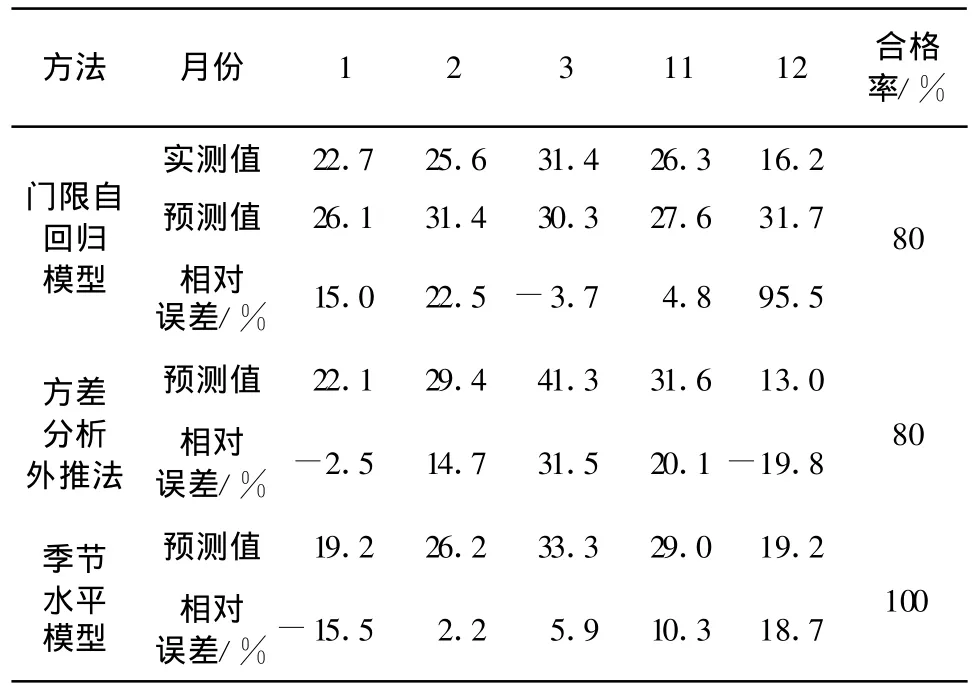
表3 TAR模型、方差分析外推法和季节水平模型预测2004年枯季月径流效果

从表3看出:对于枯季径流的预测,季节水平模型预测效果最好,也为100%,可作为今后黄土地区枯季月径流预测的主要方法。方差分析外推法次之(80%),TAR模型预测合格率虽然也是80%,但多项相对误差大于前者,因此预测效果不如前二者。这与状头站预测结果是一致的。

图3给出BP模型预测张家山站2004～2005年月径流效果。

图3 BP模型模拟月径流效果图

从图3看出:BP模型对于全系列月径流预测效果尚可,也可以作为全年月径流预测的方法。汛期模拟效果较好,与状头站一致。

表4列出BP模型预测张家山站2004～2005年月径流结果。

经统计表4用BP模型预测状头站2004～2005年月径流汛期合格率同样为100%,可作为汛期月径流预报的一般方法。但全系列预测合格率仅为63%,效果一般。

表4 BP模型模拟效果表

另外,用以上方法预测月径流误差主要源于月径流序列本身,由于影响径流成因的因素有很多:如降雨、截留、填洼、入渗以及产汇流过程等[11]。和其它模型预测径流时间序列一样,单用径流序列而缺乏其它预报因子[12]难以刻画径流自身的变化,其相关度也不高,使得模型建立条件受限且系统的应用和模拟效果因之也需作进一步的完善[13]。所以,建议在今后进行径流预测时应该考虑诸多影响其成因的因素,这样其与径流之间的相关性也会变好,并且信息越多模型预测的精度也会越高。

3 结 论

综上,季节水平模型可作为今后黄土高原地区枯季径流预测的良好途径,方差分析外推法也可用于预报枯季径流,TAR模型可作为预报的参考;BP模型可当作汛期月径流预测的较好方法,也可用于全年月径流预测。综合季节水平模型和BP模型的优点可以将二者结合起来预测全年月径流序列,这样得到的预测效果将会非常好。

[1]包为民.水文预报(第三版)[M].北京:中国水利水电出版社,2006.

[2]毛慧慧,延耀兴,张 杰.水文预报方法研究现状与展望[J].科技情报开发与经济,2005,15(19):166-167.

[3]李荣峰,冀雅珍.水文时间序列分析计算方法的研究进展与展望[J].山西水利科技,2005,(4):4-6.

[4]曹连海,胡习英,于志波.混沌神经网络在地表水资源量预测中的应用[J].水利与建筑工程学报,2005,3(4):6-8.

[5]杨叔子,吴 雅,王治藩,等.时间序列分析的工程应用(下册)[M].武汉:华中理工大学出版社,1992.

[6]陈守煜.中长期水文预报综合分析理论模式与方法[J].水利学报,1997,(8):15-21.

[7]金菊良,杨晓华,金保明,等.门限回归模型在年径流预测中的应用[J].冰川冻土,2000,22(3):231-232.

[8]焦李成.神经网络系统理论[M].西安:西安电子科技大学出版社,1996.

[9]杨行峻,郑君里.人工神经网络[M].北京:清华大学出版社,1992.

[10]Sivakumar B,Berndtsson R,Persson M.Monthly runoff prediction using phase space reconstruction[J].Hydrol Sci J,2001,46(3):377-387.

[11]卢 敏,张展羽,冯宝平.支持向量机在径流预报中的应用探讨[J].人民长江,2005,36(8):38-39.

[12]王本德.水文中长期预报模糊数学方法[M].大连:大连理工大学出版社,1993.

[13]张宏鸣,杨勤科,Li Ling-Tao,等.基于黄土高原多沙粗沙区植被恢复布局及其水文效应评价系统的实现[J].西北农林科技大学学报(自然科学版),2008,36(11):103-104.

Study on Monthly Runoff Prediction Based on Four Methods

LI Ji,LI Yi,YAN Bao-wen,SONG Song-bai
(College of Water Resourcesand Architectural Engineering,Northwest A and F University,Yangling,Shaanxi712100,China)

Runoff forecast is very important to the rational utilization and distribution of water resources.According to themonthly runoff data fromZhuangtou HydrologicStation of Beiluo River and Zhangjiashan Hydrologic Station of Jinghe River,which are two branches of Weihe River in loess plateau,the threshold auto-regressive model,neural network model,variance analysis extrapolation as well as the seasonal level model are used to predict the monthly runoff,observe the similation results and find their advantages and disadvantages.The results show that in a dry season,the eligible rates for runoff forecast by using the seasonal level model for the two stations are both 100%.Using the variance analysis extrapolation for Zhuangtou Station and Zhangjiashan Station,the eligible rates are 90%and 80%respectively.The eligible rates for runoff forecast by using the threshold auto-regressive model for the two stations are both 80%.While in a flood season,the eligible rates for runoff forecast by using the neural network model for the two stations are both 100%.This study show that the seasonal level model is applicable to the runoff forecast in a dry season.And the neural network model is suitable for the runoff forecast in a flood season,and both models have a good simulation accuracy.

threshold auto-regressive model;neural network model;variance analysis extrapolation;seasonal level model;monthly runoff prediction

TV121

A

1672—1144(2010)02—0056—04

2009-12-16

2009-12-21

李 计(1986—),男(汉族),陕西礼泉人,硕士研究生,从事水文与水资源工程方向的研究。

李 毅(1974—),女(汉族),陕西武功人,博士,副教授,主要从事农业水资源利用研究。