核心高强混凝土柱荷载-位移恢复力模型
齐 岳,郑文忠
(哈尔滨工业大学 土木工程学院,哈尔滨 150090,qiyue0451@126.com)
核心高强混凝土柱荷载-位移恢复力模型
齐 岳,郑文忠
(哈尔滨工业大学 土木工程学院,哈尔滨 150090,qiyue0451@126.com)
为建立核心高强混凝土柱的恢复力模型,在核心高强混凝土柱水平低周反复荷载试验研究的基础上,对112种工况下的核心高强混凝土柱进行计算分析和数值回归.提出以轴压比、核心高强混凝土面积比、剪跨比为参数的恢复力模型骨架曲线特征点计算公式,恢复力模型的滞回规则及卸载刚度的计算公式.按所提出的恢复力模型对试验柱进行计算,所得计算曲线与实测的滞回曲线吻合良好,说明所提出的恢复力模型具有较好的精确性,能够较好地模拟和反映构件的实际抗震性能.
核心高强混凝土柱;骨架曲线;滞回规则;卸载刚度;恢复力模型
恢复力模型是根据大量恢复力与变形的关系曲线,经适当抽象和简化而得到的实用数学模型,是进行结构弹塑性反应分析的基础[1-4].核心高强混凝土柱是指在横截面内以高强混凝土为核心,在核心区外围设置普通钢筋混凝土的柱.目前为止,尚未见到对这类柱恢复力模型的研究报道,因此,有必要对核心高强混凝土柱恢复力模型进行研究.
文献[5]已完成了9根核心高强混凝土柱水平低周反复荷载试验,测得了荷载-位移滞回曲线,分析了试验柱的耗能性能、抗力衰减、骨架曲线及延性性能.在试验研究的基础上,又编制了核心高强混凝土柱压弯构件的非线性全过程分析程序,分析了不同参数影响下核心高强混凝土柱水平荷载-位移关系曲线,并指出轴压比、核心高强混凝土面积比和剪跨比是影响核心高强混凝土柱抗震性能的主要因素.本文在上述工作的基础上,通过对112种工况下核心高强混凝土柱的计算分析和数值回归,建立了核心高强混凝土柱荷载-位移恢复力模型.
1 荷载-位移恢复力模型骨架曲线
核心高强混凝土柱荷载-位移关系曲线大致分为弹性段、弹塑性段及下降段3部分,因此,骨架曲线可采用退化三线性模型[6],如图1所示.3个特征点分别为屈服点Y、极限荷载点M和破坏点U.破坏点指水平荷载下降到极限荷载的85%时所对应的点.确定骨架曲线需要5个特征点参数,即初始阶段刚度K1、屈服后刚度K2、下降段刚度K3、水平屈服荷载Py和水平极限荷载Pu.
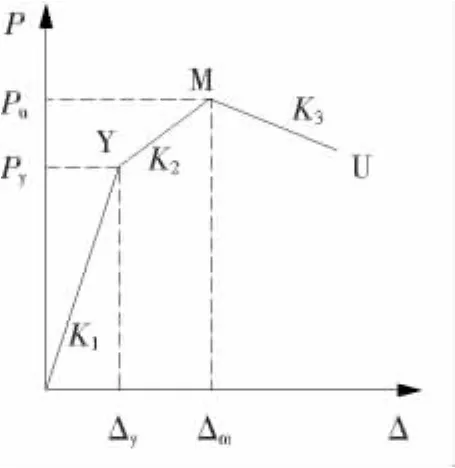
图1 骨架曲线模型
轴压比、纵筋配筋率、核心混凝土面积比(指核心混凝土面积与整个截面面积的比值)、核心混凝土强度、外围混凝土强度、配箍特征值和剪跨比等参数对核心高强混凝土柱荷载-位移关系均有影响,但其中轴压比、核心混凝土面积比、剪跨比为3个主要影响参数.在建立恢复力模型时,如果将参数全部考虑进去,虽然能够更准确地反映实际情况,但势必会导致模型计算公式的繁琐,给工程应用带来极大的不便.因此,在统计核心高强混凝土柱退化三线性模型时考虑了轴压比、核心混凝土面积比、剪跨比这3个主要影响参数,略去其他次要影响参数,这样既可以反映实际情况又便于应用.
为了得到骨架曲线上5个特征参数计算公式,对表1所示112种工况下核心高强混凝土柱的荷载-位移曲线进行了计算,图2为计算模型截面示意图.除表1中3个参数外,其他参数的取值为:核心高强混凝土柱外围截面尺寸B×H=1 000 mm×1 000 mm,核心高强混凝土强度等级为C 80,外围普通混凝土强度等级为C 30,纵筋采用25钢筋,每侧 9根,纵筋配筋率为 ρ=1.57%,箍筋采用φ12钢筋,配箍特征值λv取为0.11.表1中核心混凝土面积比R的变化是通过改变核心混凝土截面尺寸来实现的,R=0. 25,0. 36,0. 49,0.64对应的核心混凝土截面尺寸分别为 500 mm ×500 mm,600 mm ×600 mm,700 mm ×700 mm,800 mm ×800 mm,剪跨比λ的变化是通过变换柱高来实现的,λ = 3,3. 5, 4,4.5对应的柱高分别为 6, 7, 8,9 m.

表1 模型特征参数的计算工况

图2 计算模型截面示意图
通过对计算结果的整理和回归分析,建立了核心高强混凝土柱骨架曲线退化三线性模型特征参数的计算公式.图1中5个特征参数的计算公式统一由式(1)表示[7],各系数见表2.

式中:X为5个特征参数的量纲一化结果,其中初始阶段刚度K1除以柱的刚度K进行量纲一化,K按式(2)计算;屈服后刚度K2和下降段刚度K3均除以初始阶段刚度K1进行量纲一化;水平屈服荷载Py和水平峰值荷载Pu均除以fcBH进行量纲一化;fc为外围混凝土抗压强度;B为柱截面宽度;H为柱截面高度.

式中:L为柱高;EI为柱截面抗弯刚度,EI=E1I1+E2I2;E1、E2分别为核心高强混凝土和外围普通混凝土的弹性模量;I1、I2分别为核心高强混凝土和外围普通混凝土的截面惯性矩,
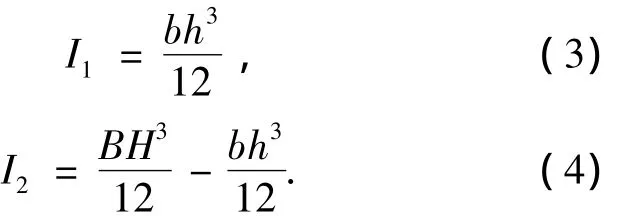
式中b、h分别为核心高强混凝土部分的截面宽度和高度.
表2中的系数是回归得到的.对表1中的112种工况进行分析后,可得到112组特征参数值,即式(1)中等号左边X值.以式(1)为回归模型,采用Matlab语言编制回归分析程序,对112组恢复力模型骨架曲线特征参数进行了回归分析,便得到式(1)中各系数.

表2 式(1)中的系数
用上述确定恢复力模型骨架曲线的方法对文献[5]中的9根试件进行了计算,所得计算曲线与试验骨架曲线的对比如图3所示.可以看出:恢复力模型骨架曲线与试验骨架曲线吻合较好,说明所提出的特征参数计算公式具有较好的精度.
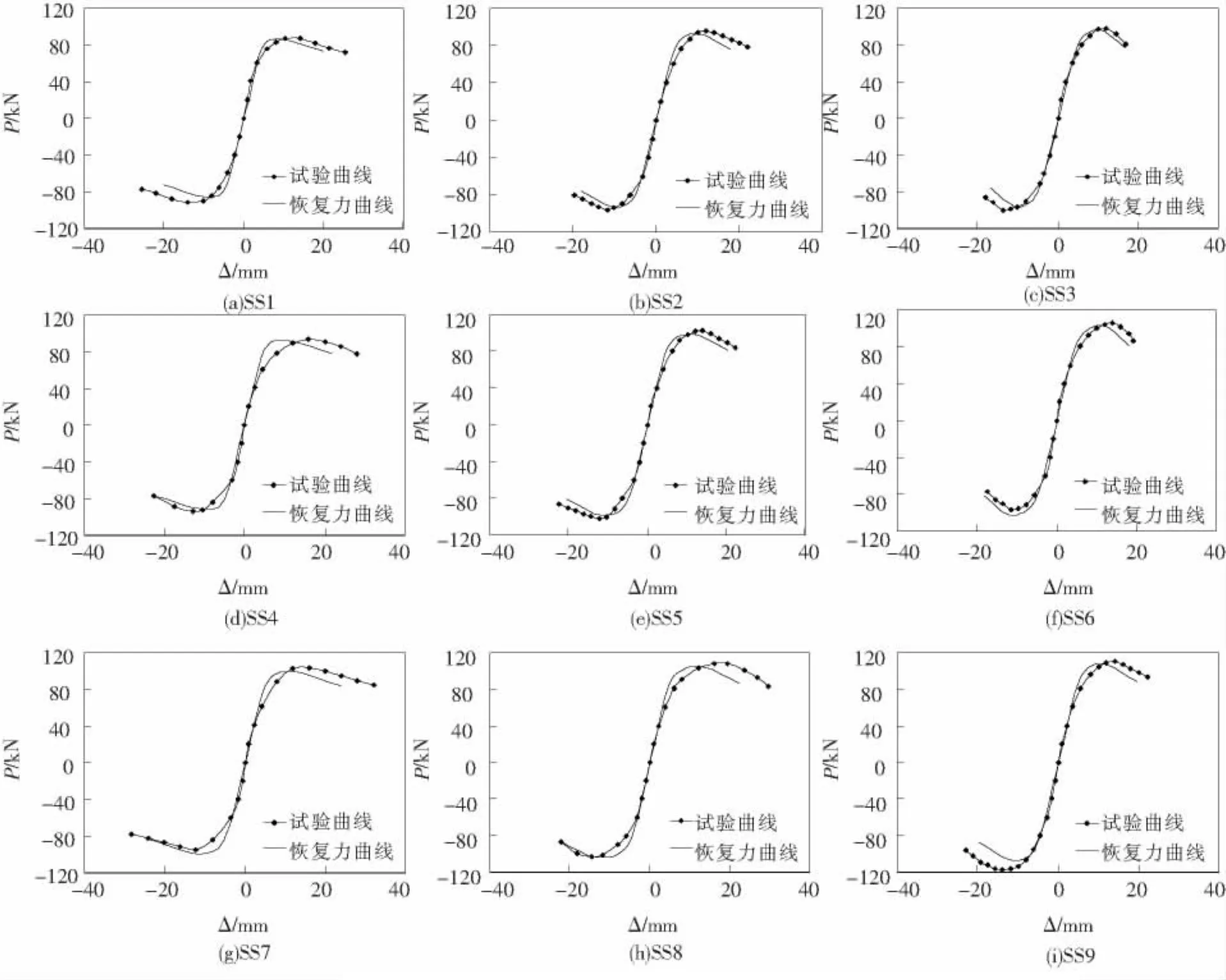
图3 试验骨架曲线与恢复力模型骨架曲线的对比
2 滞回规则
图4所示为核心高强混凝土柱P-Δ滞回规则,图中从小到大的数字表示模型在正、反向加载及卸载过程中的行走路线[8].滞回规则表述如下:
1)弹性段加载及卸载规则
恢复力未达到Py之前(1点或4点),构件处于弹性阶段,按弹性刚度加载、卸载,不考虑刚度退化和残余变形.加载及卸载路线沿着恢复力模型骨架曲线进行.
2)弹塑性段加载及卸载规则
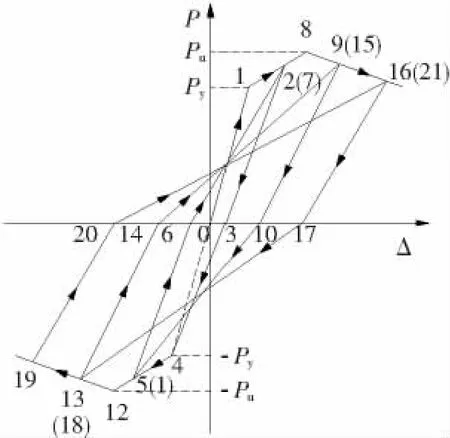
图4 滞回规则
当恢复力超过正向或者负向的屈服荷载Py,但未达到正向或负向的极限承载力Pu时,加载刚度取屈服后刚度K2;卸载刚度Kun为初始刚度的折减,根据试验结果统计回归可得卸载刚度Kun的计算公式为

式中:Δy为屈服位移;Δun为卸载位移.
卸载刚度Kun的确定方法如下[9-11],图 5 为试验柱滞回曲线的某一滞回环,其卸载刚度取卸载时刻对应的位移点与零荷载点连线的斜率.按上述原则统计出试验柱各滞回环的卸载刚度,经过回归分析可得卸载刚度计算公式即式(5).图6为刚度比Kun/K1与位移比Δun/Δy之间的关系,可以看出,卸载刚度计算公式具有较好的精度.
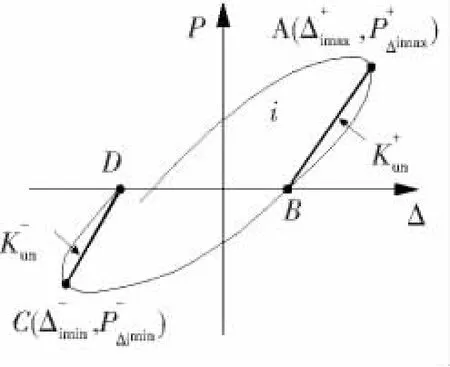
图5 滞回环的卸载刚度
3)下降段加卸载规则恢复力超过正向或负向的极限水平荷载Pu后,加载刚度取骨架曲线下降段刚度K3;在下降段开始卸载的卸载刚度仍按式(5)计算.
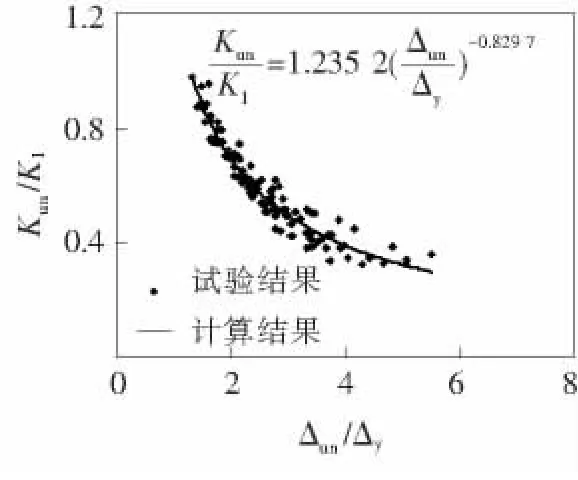
图6 刚度比与位移比之间的关系
4)反向加载及正向再加载规则
正向卸载后的反向再加载时,当反向经历过的最大位移未超过屈服位移时,从P=0处直接指向反向屈服点,当反向经历过的最大位移超过屈服位移时,从P=0处直接指向反向经历过的最大位移点;反向卸载后正向再加载时,从P=0处直接指向正向经历过的最大位移点.
3 恢复力模型与试验结果比较
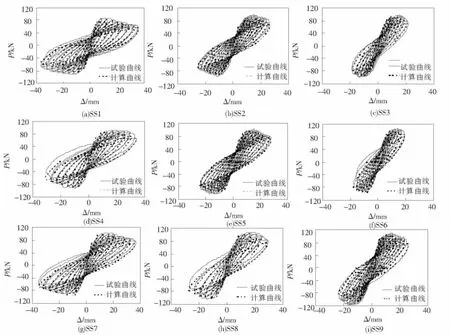
图7 恢复力模型与试验滞回曲线的对比
用所提出的荷载-位移恢复力模型确定方法对文献[5]中的9根试件进行了计算,所得计算曲线与实测滞回曲线的对比如图7所示.可以看出,恢复力模型与试验实测的滞回曲线吻合良好.说明本文提出的核心高强混凝土柱恢复力模型具有较好的精确性,能够较好地模拟和反映构件的实际抗震性能.
4 结论
1)通过对112种工况下核心高强混凝土柱的计算分析和数值回归,提出了以轴压比、核心高强混凝土面积比、剪跨比为参数的恢复力模型骨架曲线特征点计算公式.按公式计算得到恢复力模型骨架曲线与试验所得骨架曲线吻合良好.
2)通过对试件各滞回环卸载刚度的统计分析,回归得到了卸载刚度的计算公式,并提出了恢复力模型的滞回规则.
3)按本文提出的恢复力模型对试验柱进行了计算,所得计算曲线与实测的滞回曲线吻合良好,说明本文提出的核心高强混凝土柱荷载-位移恢复力模型具有较好的精确性,能够较好地模拟和反映构件的实际抗震性能.
[1]ZHENG Wenzhong,WANG Kun,ZHANG Geming.Experimental study on hysteretic behavior of prestressed truss concrete composite beams[J].Earthquake Engineering and Engineering Vibration, 2010,9(1):65-74.
[2]PANDEY G R,MUTSUYOSHI H,MAKI T.Seismic performance of bond controlled RC columns[J].Engineering Structures, 2008,30(9):2538-2547.
[3]OZCEBE G,SAATCIOGLU M.Hysteretic shearmodel for reinforced concrete menbers[J].Journal of Structural Engineering,ASCE, 1989,115(1):132-148.
[4]王文达,韩林海.钢管混凝土框架实用荷载-位移恢复力模型研究[J]. 工程力学, 2008,25(11):62-69.
[5]齐岳,郑文忠.低周反复荷载下核心高强混凝土柱抗震性能试验研究[J].湖南大学学报(自然科学版), 2009,36(12):6 -12.
[6]徐超,张耀春,卢孝哲.方形设肋薄壁钢管混凝土柱的恢复力研究[J].哈尔滨工业大学学报, 2008,40(4):514-520.
[7]陈轩.FRP约束钢筋混凝土圆柱恢复力模型的研究[D].哈尔滨:哈尔滨工业大学,2009.
[8]ZHENG Wenzhong,JI Jing.Dynamic performance of angle-steel concrete columns under low cyclic loading- II:Parametric study[J].Earthquake Engineering and Engineering Vibration, 2008,7(1):67-75.
[9]WATSON S,ZAHN F A,PARK R.Confined reinforcement for concrete columns[J].Journal of Structural Engineering, 1994,120(6):1798-1824.
[10]WATSON S,PARK R.Simulated seismic load tests on reinforced concrete columns[J].Journal of Structural Engineering, 1994,120(6):1825-1849.
[11]李国强,崔大光.钢骨混凝土梁柱框支剪力墙试验与恢复力模型研究[J].建筑结构学报, 2008,29(4):73-80.
Restoring-force model of load versus displacement for concrete columns with high strength core
QI Yue,ZHENG Wen-zhong
(School of Civil Engineering,Harbin Institute of Technology,Harbin 150090,China,qiyue0451@126.com)
In order to establish a restoring-force model for concrete columns with high strength core,based on the low cyclic loading tests.112 concrete columns with high strength core were calculated and the results were regressed.The expressions for characteristic nodes of the skeleton curve were given in terms of the axial compression ratio,the area ratio of core high strength concrete and the shear-span ratio.In addition,the hysteretic rule of the restoring-force model and the expression for unloading stiffness were presented.The numerical results based on the restoring-force model given in this paper are in good agreement with experimental results,which shows that the restoring-force model presented in this paper can accurately simulate and reflect the seismic behaviors of concrete columns with high strength core.
concrete columns with high strength core;skeleton curve;hysteretic rule;stiffness of unloading;restoring-force model
TU375.3
A
0367-6234(2010)04-0531-05
2009-03-03.
国家科技支撑计划子课题(2006BAJ03A10-07);国家
教育部长江学者奖励计划资助项目(2009-37).
齐 岳(1982—),男,博士研究生;
郑文忠(1965—),男,博士生导师,长江学者特聘教授.
(编辑 刘 彤)

