GPS在机载雷达测速精度鉴定中的应用*

王云河,王存良

(1.中国人民解放军海军驻郑州地区军事代表室,河南郑州450015;2.中国电子科技集团公司第二十七研究所,河南郑州450007)

0 引 言

GPS在航天测控和外弹道测量等方面的应用已有很多文章论述过,但应用于机载雷达测速精度鉴定,未见其公开发表。机载雷达测速是指利用机载雷达测量空中飞行目标的速度,对于低空、超低空飞行目标,地面雷达难以发现;机载雷达能够胜任,常用于预警探测,也可用于飞机编队飞行。机载雷达测速的特点是雷达本身随飞机运动,在探测运动目标的速度时要考虑飞机本身的速度,又由于速度是矢量,机载雷达测的是目标与飞机连线上的速度,还需要将测得的目标速度转换成地速,所以,技术实现较为复杂。测速精度包括速度数值大小的精度和速度方向的精度,速度方向的精度实际上是测角精度,测角精度鉴定可用常规方法,精度常用标准差表示。机载雷达测速精度鉴定的传统方法,是利用外弹道测量(简称外侧)设备,在飞行目标和飞机上各装一台应答机,机载雷达和三个站的外测设备同时测量目标速度,这三个站的外测设备还要同时测量目标的位置,还需要另外三个站的外测设备同时测量飞机的位置速度,最后转换到机载雷达径向(机载雷达与目标机的连线)方向上进行速度值精度计算。利用GPS鉴定机载雷达测速精度,需要两台高动态的GPS接收机分别装在飞机和飞行目标上,一台GPS接收机在地面作为差分基准。机载雷达测速精度鉴定的两种方法比较如表1所示。

表1 机载雷达测速精度鉴定的两种方法比较

由表1可知,GPS方法与多站外侧方法相比,计算过程稍微简单,所需设备、参试人员、经费投入和所需时间,都有明显优势。

以某一工程应用为背景,用GPS接收机测量目标机的运动速度作为机载雷达测量目标机速度的基准值,鉴定机载雷达测量目标机运动速度的精度。着重介绍了GPS接收机测量目标机的运动速度,在机载雷达径向方向上的速度计算过程,给出了速度基准值精度的计算公式,并做了具体计算,结果表明,其精度满足作为标准值的要求,即大于3倍的被测设备精度[1]。工程应用中,在考虑精度鉴定方案时,首先应考虑作为标准值的精度要大于3倍的被测设备精度,其次还要将标准值与被测值转化到同一方向上,应满足在同一方向上标准值的精度大于3倍的被测设备精度。在以往的工程应用中,由于将GPS接收机测得的目标机速度转换成雷达与目标机的径向速度,其计算较为复杂,又因为时间紧迫,所以忽略了转换后的径向速度精度计算。因此,不仅论述了测速精度鉴定时应考虑的问题及解决方案,而且也是对以前所做方案可用性的论证。

1 GPS接收机测量目标机速度作为基准值鉴定测速雷达精度

差分GPS的测速精度为0.1 m/s,定位精度L、B为5～10 m,H 为10～20 m;某机载雷达测速精度假定为1 m/s,显然,差分GPS的测速精度满足作为该机载雷达测速的基准要求;但该机载雷达测目标机的速度是雷达与目标机的径向速度,所以需要将GPS测得的目标机速度转换成雷达与目标机的径向速度,而且需要计算转换后的径向速度的精度,看是否满足精度要求,从而决定精度鉴定试验方案。

1.1 GPS得到的目标机速度转换成雷达与目标机的径向速度

目标机上的GPS接收机测得目标机速度是在东北天坐标系下,为(V E,V N,V H),测得目标机位置为(L,B,H),雷达载机上的GPS接收机测得雷达载机位置为LP,BP,H P,要求两台GPS接收机时间同步;将(V E,V N,V H)转换成目标机对雷达的径向速度,计算步骤如下

1)将目标机位置(L,B,H)、雷达载机位置(LP,B P,H P),分别转换成地心空间直角坐标(X m,Y m,Z m)和(X P,Y P,Z P)[2]140 m。

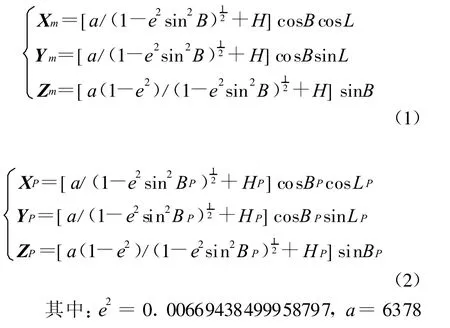
2)将目标机的地心空间直角坐标(Xm,Ym,Z m)转换成雷达载机所在位置的北西天坐标(X g,Yg,Z g)[3];

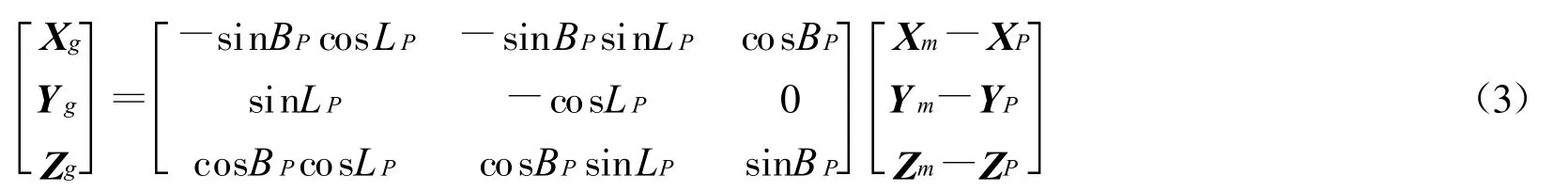
3)将目标机的东北天坐标系速度(V E,V N,V H)转换成北西天坐标系速度(﹒X N,﹒Y W,﹒Z H);

4)将目标机的北西天坐标系速度(﹒X N,﹒Y W,﹒Z H)转换成地心空间直角坐标速度(﹒X m,﹒Y m,﹒Z m);

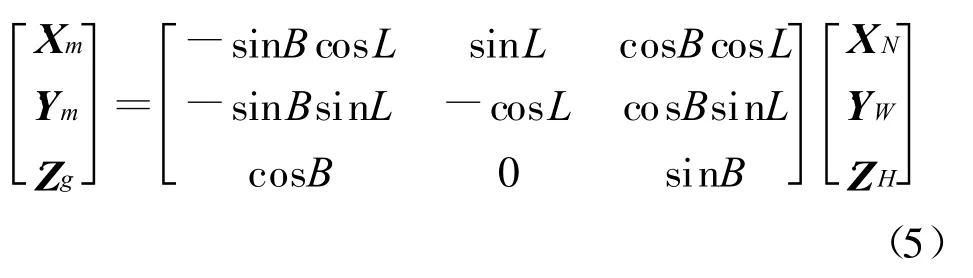
5)将目标机的地心空间直角坐标速度(﹒X m,﹒Ym,﹒Zm)转换成以雷达载机所在位置的北西天坐标系速度(﹒X g,﹒Y g,﹒Z g);

7)将式(3)和式(6)带入式(7),可得到目标机对雷达的径向速度V

1.2 雷达与目标机径向速度基准值的精度计算公式

这里提到的精度是指标准差σ,它是方差σ2的正平方根值;由式(7)得到[1]

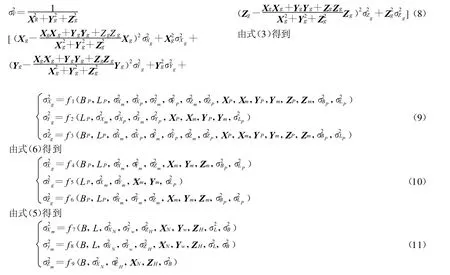
式(9)、(10)、(11)中由于其解析式较为复杂,占用篇幅太多,故在此略去,只表示了函数中有哪几个自变量;在计算测速精度时,应将L、B的精度5～10 m转换成弧度,这时要考虑目标机和雷达载机的高度。目标机和雷达载机的地心空间直角坐标位置精度应由式(1)和式(2)推导出来,并根据L、B、H的数值及精度算出具体数值,由于文章篇幅所限略去了这些内容。将式(9)、(10)、(11)代入式(8)即得到径向速度的方差,再开方就得到了径向速度的精度[1]。

2 径向速度基准值及其精度计算

2.1 径向速度基准值计算

某一试验中有一组数据,载机的地心大地坐标(103.1003705°,39.1845835°,8719.1885),目标机的地心大地坐标(99.936546°,40.483662°,3253),北向速度为10.252000 m/s,东向速度为216.914993 m/s,天向速度为53.188000 m/s。用Excel作为计算工具,按照第1.1节中的计算步骤先后计算出以下数据如表2)。

利用上表中的最后一行(两组)数据由式(7)算出径向速度V=-188.2410518053 m/s;此时刻机载雷达测得的目标与雷达的径向速度VRD=-187.974655 m/s,二者相差-0.2664 m/s,初步判定满足测速精度基准要求。

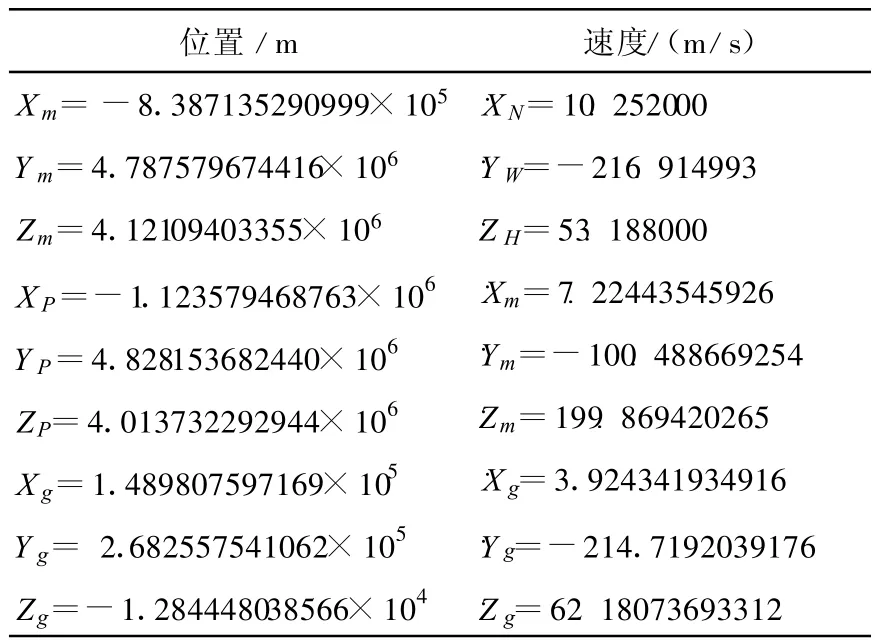
表2 位置和速度计算结果

2.2 径向速度基准值精度计算

用Excel作为计算工具,仍按第2.1节(径向速度基准值计算)中的条件,可直接用第2.1节中的部分计算结果。载机和目标机的L、B精度按10 m考虑,转换成弧度其精度分别为 σLP=2.021 428333593×10-6、σBP=1.567459739330 ×10-6、σL=2.062280420138 ×10-6、σB=1.568803895277×10-6,计算得到的数据如表3所示。

利用本节得到的数据代入式(8)计算径向速度的方差,其算术平方根即为径向速度的精度,计算结果为σV=0.10029 m/s;显然完全满足作为鉴定速度精度值1 m/s的基准值要求。

表3 精度计算结果

3 结 论

径向速度基准值计算步骤及公式,经过若干组数据代入计算,结果表明是正确的,而且已经用于某一工程的试验数据处理,效果令人满意;后来用于多个型号机载雷达的测速精度鉴定,取得了较好的效益。特别是径向速度基准值精度计算公式的推导及数据代入计算,以前没有做过,所以这一内容也是对以前工程应用的有力佐证。虽然只用了一组数据来计算径向速度基准值的精度,但是对已知的定位精度L、B为5～10 m,H为10～20 m,在计算时取定位精度L、B为10 m,H为20 m,即按最低精度代入计算的,而且计算所得的精度远超过应用要求;所以完全可以作为测速基准值。

[1]肖明耀.实验误差估计与数据处理[M].北京:科学出版社出版,1980.

[2]张守信.外弹道测量与卫星轨道测量基础(第二版)[M].北京:国防工业出版社,2001.

[3]陈芳允主编.卫星测控手册[M].北京:科学出版社出版,1992.