非相关平行机台的间断批量和计划排序研究
陈驻民, 羊 英
(1.东华大学 管理学院,上海 200051;2.上海第二工业大学,上海 201209)
0 引言
混合流程生产的概念产生于70年代[1],是指包含若干个生产阶段或工作中心,每个生产阶段或工作中心都有平行机器[2]。某些生产阶段可能只由一个设备,但是至少有一个生产阶段必须有多个设备。每个产品必须在每个生产阶段的至少一台机器上进行加工处理。本文研究的是混合流程型企业的间断批量和计划的定制问题。该问题是一个同时考虑批量和计划问题,对于该问题的研究引起了很多研究者的关注[3~7]。文献[8]解决的问题是相同平行机的批量和计划问题,考虑的是固定的装设成本,而且没有延期的发生,文献[9]提出了解决单个机器及相同平行机的方法。本文采用文献[8]提到的方法解决间断批量和计划排序,本文以纺织企业为例,考虑的是非相同平行机的问题,很好地解决了与纺织企业具有相似特征的相似产品在非相关平行机上的混合流程型企业的间断批量和计划排序问题。
1 算法描述
本文的启发式算法涉及如下几个概念:空闲区—指在未分配生产任务的加工机器上连续的空闲天数,完成生产订单 I,需要产品j1的数量为nj1个单位,需要的加工工具为s1,最后的完成日期为DDI,算法中假定完成该订单需要6个空闲天数,如图1所示。在空闲区的描述中规定j*是不同于j1的产品,s*是不同于S1的机器。同时有以下几个表达方式需要说明:

图1 空闲区类型
1)(j1,0) 被加工的产品为j1,直到订单的截止日期有若干可用的空闲天数。
2)(s1,0) 产品j*的生产需要利用工具s1,同时直到订单的截止日期有一系列可用的空闲天数。
3)(j1,0,j*) 或 (s1,0,s*) 空闲区开始处安排生产j1或j*,需要相应的工具s1或s*,结束的时候一定是生产不同的产品j*,使用不同的工具s*。
4)(j*,0,j1)或(s*,0,s1) 空闲区开始处安排生产j*,需要相应的工具s*,结束的时候一定是生产不同的产品j1,使用不同的工具s1。另外,空闲区是不固定的,或者在开始,或者在结束,对于不同的产品也可以使用同样的工具。
该算法有以下三个步骤:1)选择生产订单,2)选择一个空闲区域用于指派产品订单,3)把一个产品订单分配到空闲区域。具体算法如下。在批量和计划制定开始之前,先把生产订单进行排序,产生生产订单列表。该列表可以细分成不同的子列表,相同的订单截止日期可以组成一个子列表。
1.1 选择一个生产顺序
产品的生产顺序是由给定的生产列表制定的,生产列表的顺序是由不同的优先规则制定的,可以采用如下几种优先规则:
1)处理生产订单的机器数量
该规则是通过增加可以用来进行生产的机器数量来安排生产订单。这样可以避免一些小订单(只需要几台机器)不会总排斥在计划外。
2)生产订单的规模
采用这个规则,可以降序安排订单大小。采用此规则,可以使总的生产规模最大化。另一方面,该规则的一个最大的缺点是把小的订单总是排斥在计划之外。
3)参考以前计划中的优先级
采用该规则,从上个月制定的计划中检查最后几台机器的排序情况,选择同样类型的订单最先排序,采用该方法可能会得到最小的换设频率。
4)由用户定义优先级
用户可以根据他想要的顺序定义订单的优先级。
1.2 给选定的空闲区分配订单
选定的生产订单分配到空闲区域,采用的是后溯或前溯计划的方法。先介绍几个符号定义:
1)DDI:产品I的订单截止日期;
2)Nj1,I:生产订单I的产品j1的计划生产数量;
3)u:空闲区的长度,例如:连续空闲的天数;
4)h: 空闲区的第一天;
5)pj1,m:产品j1在选中的空闲区机器m上的生产率;
6)ls1:机器工具的使用寿命,用百分数来表示;
7)wsi,j1,m:在机器m 上生产产品1天的其工具的损耗,用百分数来表示。具体方法如下:前溯计划:
1)分配产品j1到空闲区的第一天;
2)空闲区天数=空闲区天数-1;
3)订单上的数量= 订单上的数量-产品j1在机器m上的生产率;
4)工具的使用寿命=工具的使用寿命-在机器m上生产产品j1一天的损耗;
5)如果u=0 或nj1=0 或ls1=0 结束程序否则转到step2;
后溯计划:
1)分配产品j1给后一个空闲区的第一天(h+u-1);
2)空闲区天数=空闲区天数-1;
3)订单上的数量= 订单上的数量-产品j1在机器m上的生产率;
4)工具的使用寿命=工具的使用寿命-工具在机器m上生产产品j1一天的损耗;
5)如果u=0 或nj1=0 或ls1=0 结束程序否则转到2)。
1.3 为生产订单的分配选定一个空闲区域
在选择了生产订单算法,并且把生产订单分配给一个机器以后,采用以下的算法进行:
假设当前正在加工的产品为产品D和产品B,正在使用的工具是S1。
1)如果存在[j1,0]或[j1,0,j*]或[j*,0,j1]空闲区,则转到2),否则如果存在[s1,0]或[s1,0,s*]或[s*,0,s1]则转到3),否则选择有最大空闲天数的空闲区u,然后采用后溯计划方法;
2)如果存在[j1,0]或[j1,0,j*],则采用前溯计划方法,否则如果存在[j*,0,j1],则采用后溯计划方法;
3) 读取正在使用工具s1加工的产品D和产品B;
4)读取可用的空闲区[s1,0];[s1,0,s*];[s*,0,s1]);
5)读取将要被插入空闲区的产品型号d或b;
6) 如果(D;[s1,0]或[s1,0,s*];d)或(B;[s1,0]或 [s1,0,s*];d)或(B;[s1,0]或[s1,0,s*];b) 则采用前溯计划方法,否则如果(D;[s*,0,s1];d)或(D;[s*,0,s1];b)或(B;[s*,0,s1]);b) 则采用后溯计划方法,否则选取有最大空闲天数的空闲区后采用后溯计划方法。
该算法尽力寻找现在正在被机器所加工的相同产品订单,如果订单中不存在和正在处理的产品相同的订单则去找寻使用相同工具的的订单,如果上述两种情况都没发现,则采用后溯计划方法寻找更大的空闲区间。
2 算法示例
考虑如下的例子,要在4台机器上安排8个订单,订单的排序及其订单内容如表1所示。生产过程中要考虑如下假设:
1)机器换设的原因是生产的产品使用的工具发生改变,或者工具的自然磨损。
2)工具的磨损为每天10%
3)生产线的生产能力为每天10个单位
4)订单的排序可以采用多种方式安排其优先级

表1 排序后订单
开始时,即上一个计划的最后一天,机器1加工的产品是产品a,所用的工具是X,剩余80%的耐耗时间,机器2 加工的产品是产品c,工具是Y,剩余30% 的耐耗时间,机器3加工的产品是产品f,所用的工具是Z,剩余70%的耐耗时间,机器4加工的产品是产品g,所用的工具是X,剩余50%的耐耗时间。采用本文的算法,可得到如下的结果,如图2 所示:

图2 采用启发式算法的结果
图2中给出的排序订单8中的产品g有10个单位的生产任务由于超过了其生产能力而未被安排。
本文以某纺织企业为例,表2给出了实际生产系统中某月的订单情况。
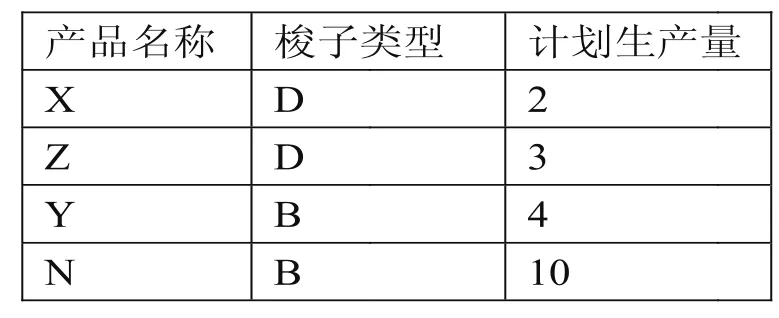
表2 某月定单情况

表3 实际系统与采用启发式算法的比较
从表3中可以看出,采用该启发式算法可以使换设次数和拖期率都能得到明显改善。
3 结论
本文给出了一个求解混合流程企业中非相关平行机的间断批量和计划排序的启发式算法,该算法的目的是最小化换设频率,其间考虑生产能力,工具的自然损耗,订单的优先级排序以及订单的最后截止日期等限制,采用此方法能够较方便地同时解决生产中批量的规划和生产排序问题。
[1] T.S.Arthanary,K.G.Ramaswamy,An extension of two machine sequencing problems[J].Operations Research8(1971)10–22.
[2] S.E.Elmaghraby, R.E.Karnoub, Production control inflexible flowshops:anexamplefromtextile manufacturing[C].OR ReportNo.305ORand IE Department,NorthCarolina State University,USA,1995.
[3] Salomon,M.,Kroon,L.G.,Kuik,R.,&VanWassenhove,L.N.(1991).Some extensions of the discrete lotsizing and scheduling problem[J].Management Science,37,801–812.
[4] Drexl, A.,& Kimms,A.(1997).Lot sizing andscheduling—Survey and extensions[J].European Journal of Operational Research,99,221-235.
[5] Fleischmann,B.(1990).The discrete lot-sizing and problem[J].European Journal of Operational Research,44,337-348.
[6] Staggemeier,A.T.,Clark,A.R.(2001).A survey of lot and scheduling models[C].Proceedings of the 23rd Annual Symposium of the BrazilianOperational Research Society(SOBRAPO),Brazil (938–947).
[7] Kuik,R.,Salomon, M.,&VanWassenhove,L.N.(1994).Batching decisions: Structure andmodels[J].European Journal of Operational Research,75,243-263.
[8] Pattloch,M.,Schmidt,G.,&Kovalyov,M.Y.(2001).algorithms for lot size scheduling with application in the tobacco industry[J].Computers and Industrial Engineering,39,235-253.
[9] Blazewicz,J.,Ecker,K.,Pesch,E.,Schmidt,G.,Weglarz,J.(1996).Scheduling computers and manufacturing processes[C].Berlin:Springer.

