浅析水库中长期水文预报方案的编制——以泽雅水库为例

徐启宝,许尔金

(1.温州宏源水电建设有限公司,浙江 温州 325000;2.温州市泽雅水库,浙江 温州 325023)

中长期水文预报一般采用数理统计方法、天气学方法、非大气因子方法3个方法来编制。在此采用数理统计方法。

数理统计方法大体分为单要素分析和多要素分析。多要素分析方法相关因素多,分析较为复杂,因而在此不作分析。本文只简单介绍单要素预报方法中的“周期迭加与周期分析法”。

1个水文要素随时机变化过程线的外形尽管多种多样,但是总可以把它看成是几个具有不同周期的周期波重叠而成。其数学模型为:

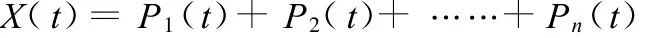
其中:X(t)为水文要素的时间序列;

P1(t)、P2(t)为周期波动的序列。

这样,只要根据实测资料,分析出它含有的几个周期,并且假定这些周期在未来的一段时间内仍然保持不变,就可以根据分析出来的周期分别进行外延迭加而进行预报。这就是应用周期迭加进行预报的概念。显然,这个方法的关键是周期分析。

1 用方差分析法作周期分析的原理

水文要素存在着周期性变化的事实,早已为人们所揭露。当然,由于水文要素的历史演变受到各种因素的影响,它不可能象天体运动、潮汐等现象具有严格的周期,而只是概率意义上的周期,也就是只能理解为某一现象出现之后,经过一定的时间间隔,这种现象重复出现的可能性较大而已。由于各种水文要素过程线的外形比较复杂,不能很清楚地判断它是否存在某种周期,因此需要利用各种周期分析来确定周期。周期分析应解决的问题是:这一要素存在着周期变化;如果存在周期变化,确定周期;分析周期的可靠性。

周期分析的方法很多,在此采用方差分析的方法来分析周期。

1.1 利用方差分析作周期分析的基本概念

方差分析就是将此序列X(t)按不同的可能周期2、3、……、k进行分组排列。计算各个试验周期中组间与组内的方差比来确定存在那个周期。

在介绍方差分析之前,先来看1个假设具有5 a严格周期的特例。设某站有一要素具有20 a的资料,其数据见表1。

设有一时间序列X(t),共有n年实测资料x1,x2,……,xn。如果它存在周期时,则可能的周期为 2、3、……、k,

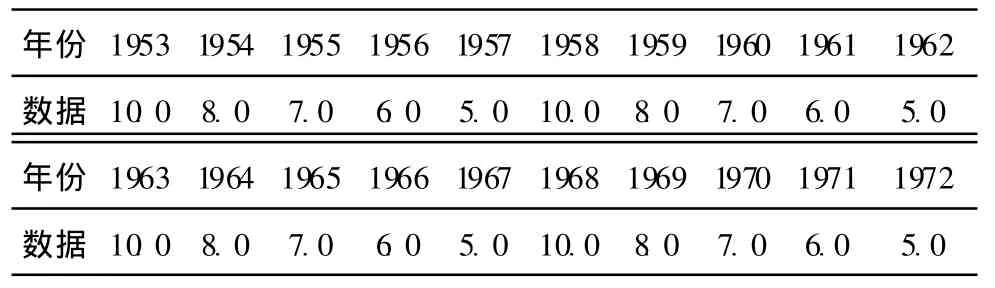
表1 5 a严格周期的特例20 a的资料表

如果将它按照5 a严格周期分组排列成表2时:

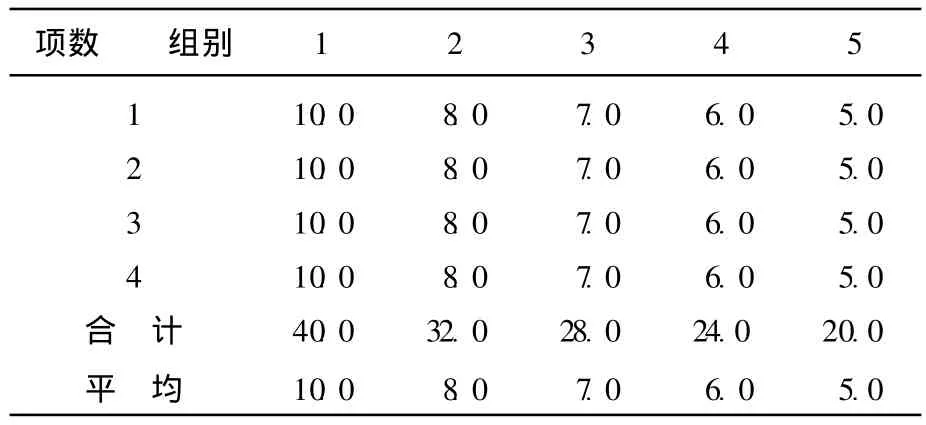
表2 5 a周期分组排列表

由表可见,各组组内的数据都一样,没有差异,而各组组平均值之间的差异却较大。

如果不按它的5 a严格周期排列,而按另一种年份 (比如4 a)分组排列如表3时,则可以看出,各组组平均值完全相同,没有任何差异,而同组内各个数据却差异较大。

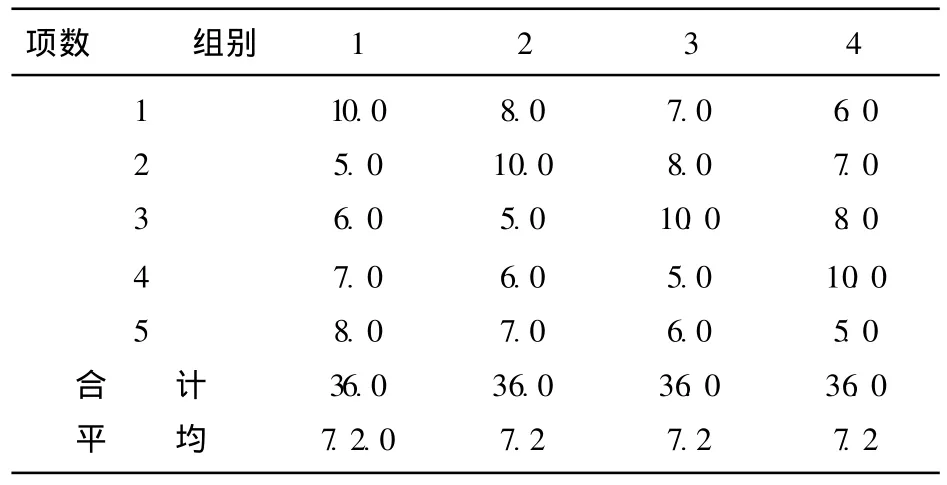
表3 4 a周期分组排列表

就一般情况而言,1个站的某一要素如果存在着周期性变化时,那么把它的历史资料按其存在的周期分组排列时,处在同一组内的各项数据应该是处在同一位项下的观测值。而不同组的数据则是处在不同位项下的观测值。由于在各个周期的高峰时期所观测到的数据平均来说是比较大的,而在各个周期的低谷时期所观测到的数据平均来说是比较小的,在峰谷之间的转换时期观测数据则是中等的。因此,在同组之内的数据的差异是相对较小的,而组与组之间数据的差异则是相对较大的。

反之,如果不按它的周期分组排列时,则处于同组内的资料包含着不同位相下的观测值,1组之内可能既有高峰、又有谷底和中等数据,因此同组内各项数据的差异就相对较大,而组与组之间的数据差异则相对较小。

组间与组内数据的差异情况,可以分别计算它们的离差平方和把它们表示出来。这样就可以利用计算出来的组间离差平方和与组内离差平方和进行比较,并由此推断是否有周期存在。

1.2 组间、组内离差平方和S12、S22的计算

如果将有N年资料的要素按表4分组排列时,j表示组别,j=1,2,……b,表示共分 b组。I为每组项数,i=1,2,……a,表示每组有a项。Tj为每组合计,T为总数为每组组内平均值,而 X为总的平均值。则组间离差平方和、组内离差平方和的计算公式为:

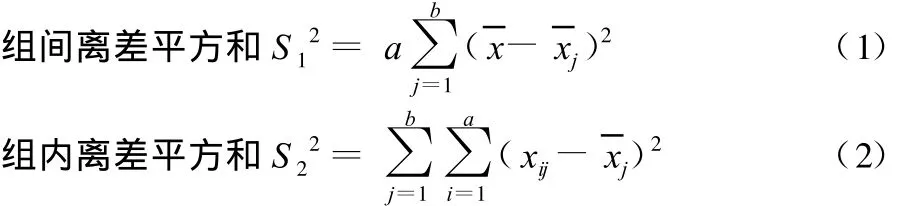
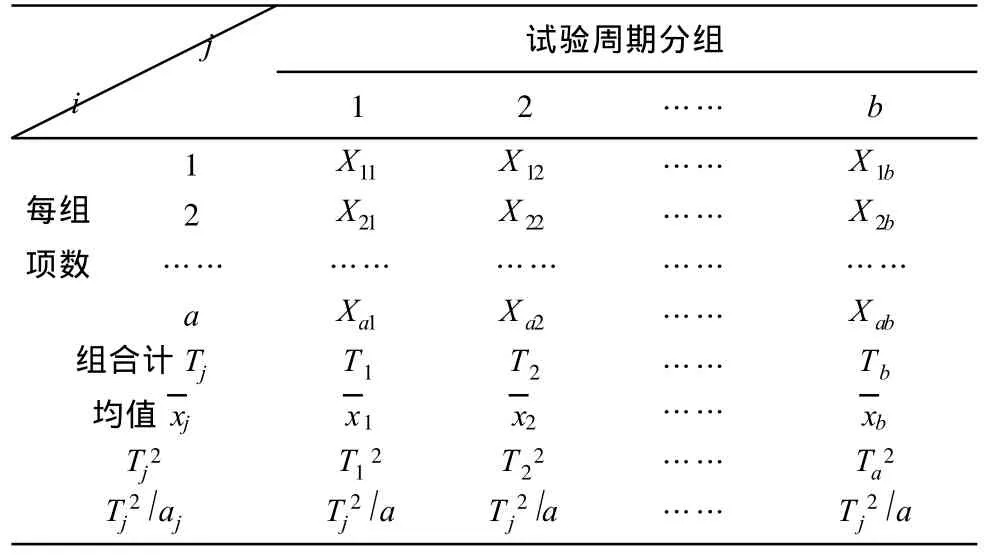
表4 试验周期分组表

由式(1)可见,组间离差平方和S12是指每组组平均值对总平均值的离差平方,再求和。,它代表了各组组平均值之间的差异前面还有1个 a,这是因为每组内又有a项的关系。

组内离差平方和是指同组之内各项数据 xij对组平均值的离差平方再求和,它代表了1组内部数据之间的差异,由于共b组,所以还要把各组的相加 ,故

在实际计算时一般都用下面的式子计算,这是因为一则计算方便,二则计算误差较小。

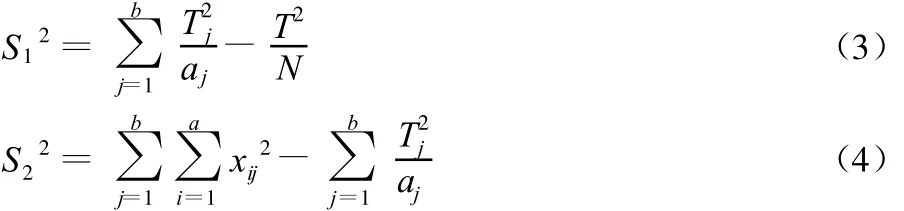
1.3 计算自由度f1、f2及F值并选定信度a

由于在分析周期时,要计算各种试验周期的S12与,而不同的试验周期在分组数目与每组含有的项数上都是不同的。为了能够相互比较,所以还要计算它们的平均情况,即平均组间离差平方和与平均组内离差平方和。

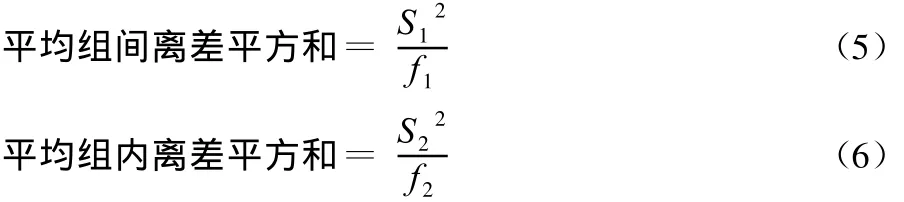
上式中f1(f1=b-1)、f2(f2=N-b)分别为组间离差平方和与组内离差平方和的自由度。

达到什么标准才算组间的平均离差平方和显著地大于组内的平均离差平方和呢?这就需要计算它们之间的比值F来确定:

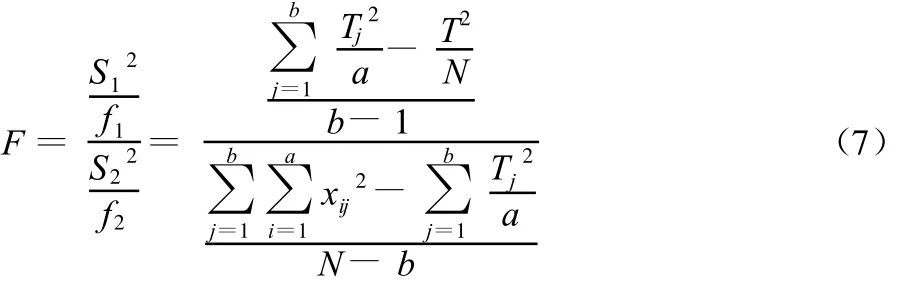
在一定的条件下,可以证明,这个比值F是一随机变量,而且它是服从F-分布的,F-分布有专用的F表可查,因此可以用F检验的方法来检验组间平均离差平方和是否显著地大于组内平均离差平方和。

在实际应用时,可先根据实测资料,用式(7)计算出F值,然后根据已知的自由度 f1、f2选定信度 a,在F分布的专门表中,查出相应的 Fa,如果:

F＞Fa则表明,在这个a水平上,差异显著,有周期存在;

F＜Fa则表明,在这个 a水平上,差异不显著,无周期存在。

以上介绍的是应用方差分析进行周期分析的基本思想,至于计算的全过程可参阅下面的实例。

2 实例分析—泽雅水库雨量中长期预报

2.1 方案的基本思路

泽雅水库1998年建库以来至今只有11 a的历史资料,为此,采用老泽雅站的水文资料 (1958年以来的),共50 a资料 (见表5)。

表5 预报2008年降水量计算表

假设:把泽雅水库的年降水量的变化过程作为一个波动过程来看待,这个波动由2个因素构成:一是由具有周期变化的周期波;二是不具有周期变化的随机波。在周期中,又认为是由几个不同周期的周期波互相叠加而成。

2.2 周期分析

周期分析根据50 a实测资料应用方差分析进行,具体计算过程如下:

2.2.1 计算各年降水量距平值 Δ Pi、Δ Pi2Δ Pi=Pi-

式中:Pi为各年的实测降水量(mm);

计算结果见表5第2、3列

2.2.2 试验周期分组排列

将各年的距平值按各种试验周期进行分组排列,泽雅水库共有50 a资料,n为奇数,=25,因此,试验周期从25 a排至2 a。泽雅水库5a周期的排列情况列表。根据表中的资料计算出各组的:组合计Tj、Tj2、Tj2/aj、均值,结果见表6。

表6 试验周期进行分组排列 (泽雅水库)表

2.2.3 计算组间、组内离差平方和S12、S22

=134 620.3+45 516.61+479 890.4+471 046.3+365 879.8=1 496 953.3

组间自由度f1=b-1=5-1=4 试验周期为5,则b=5

组内的自由度f2=N-b=50-5=45 N为观测资料年数,即 N=50

2.2.5 选定信度a

根据自由度f1、f2在F分布表中查出相应的Fa值。试验周期为5时,f1=4,f2=45,在 F分布表中查得:F0.05=2.59,F0.25=1.40。

F值:1.40＜2.08＜2.59即:F0.25＜F＜F0.05

可信度在a0.05～ a0.25

2.2.6 挑选周期

通过对5,6,7 a周期分析,6,7 a周期(分析过程在此不作介绍,结果见表5)不明显,故挑选5 a周期为泽雅水库的第1周期。

2.2.7 计算5 a周期波各年的振幅及新序列x1(t)

计算滤去5 a周期波以后的新序列x1(t):计算方法是将原序列x(t)减去5 a周期波P1(t)的序列即得,其结果见表5第6列。

2.3 余波项的计算

如前所述,把这一余波是作为符合平衡时间序列的要求来处理的。泽雅水库的前期量采用5项,其预报方程为:

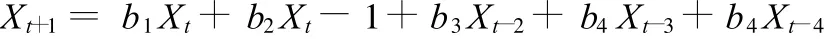
预报系数b1,b2,b3,b4,b5由下列线性方程组决定

计算过程不作介绍。计算结果:b1=0.139 055,b2=0.119 32,b3=0.113 651,b4=-0.130 08,b5=-0.26975。余波计算结果见表5第7列。

2.4 预 报

2.4.1 距平计算值的计算

将5 a周期波各项与余波各项相加所得,所得结果见表5第8列。

2.4.2 各年的预报值的计算

这种预报方法就是所谓方差分析周期迭加法。由此法计算的年降水量过程线与实测过程线的比较见图1。

3 结 论

(1)利用方差分析来分析周期时,采用了方差比F来判断周期是否显著的检验。而统计量F是有一定条件的,因此所得到的分析结果应是近似的。

(2)应用周期迭加来作预报时,应注意自然界是在不断变化和发展的,当水文要素演变的规律性发生了转折时,再用这种周期去预报时就会招致失败。

(3)应用周期迭加来作预报时,关键是分析第1周期,如果第1周期分析不可靠,那么其余周期也受影响;而且应用周期迭加来作预报时,实际上假定了分析出来的周期在未来一段时间内仍然保持,因此分析出来的周期比较稳定,才能使预报较准确。