基于向前选择变量法的我国粮食总产量多元线性回归预测模型
刘 东,白雪峰,孟 军
(1.东北农业大学水利与建筑学院,哈尔滨 150030;2.东北农业大学农林经济管理博士后科研流动站,哈尔滨 150030;3.东北农业大学理学院,哈尔滨 150030)
目前,预测粮食产量常用的方法有支持向量机、粗糙集理论、马尔柯夫模型、组合模型、模糊回归等方法[1-6],但这些方法有的精度不高,有的原理复杂。多元线性回归是一种简单实用的多元统计分析方法,已经广泛应用于社会、金融、医学以及水质预测等众多自然科学领域中[7-10]。由于区域粮食总产量受到粮食单产、粮食播种面积等众多复杂因素的制约[11-12],因此,本文尝试采用多元回归分析方法建立我国中长期粮食总产量多元线性回归预测模型,为保障我国粮食安全提供决策依据。
1 我国粮食总产影响因子变化趋势分析预测
粮食总产受到多种因素的影响,其中粮食单产、粮食播种面积、化肥施用量、有效灌溉面积、农机总动力及农田成灾面积是最为重要的6个影响因子。现选取前述6个影响因子1983~2006年序列资料(见图1、2)进行分析预测,结果见表1。
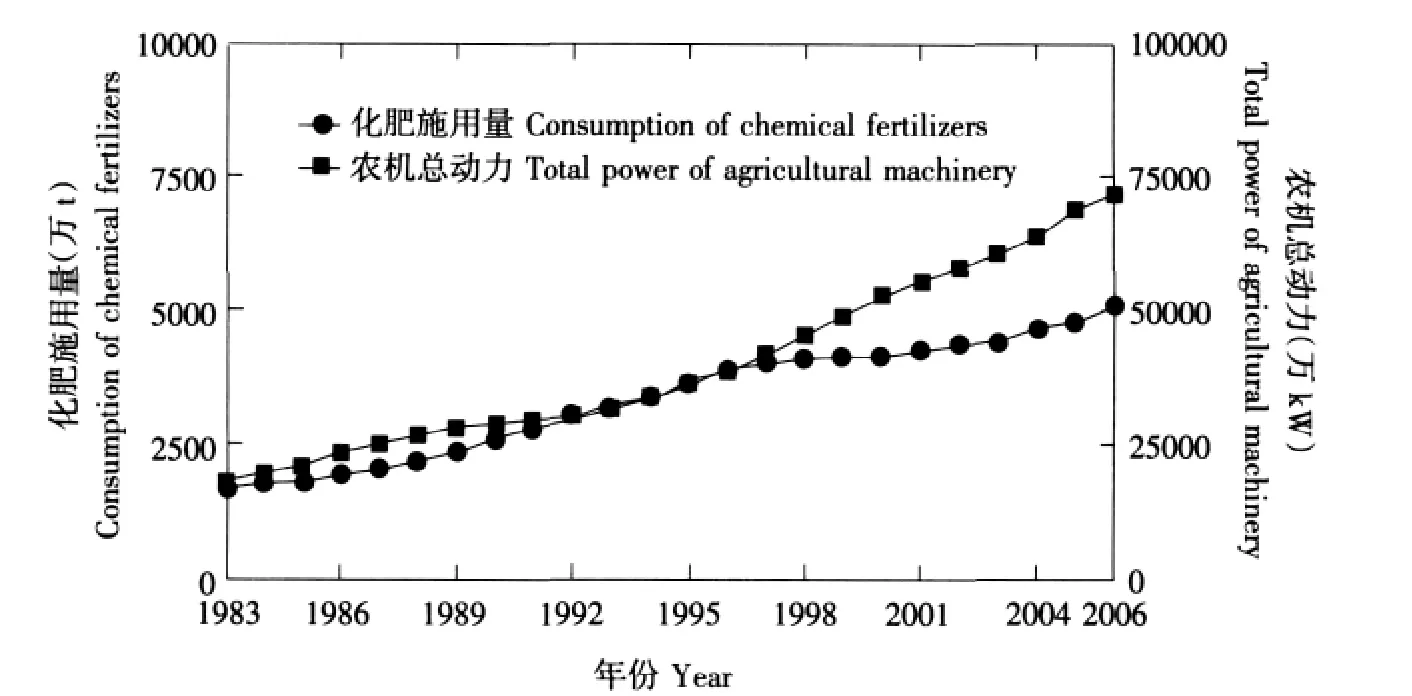
图1 我国化肥施用量与农机总动力变化曲线(1983~2006)Fig.1 Variation curve of Chinese fertilizer application rate and total power of agricultural machinery from 1983 to 2006
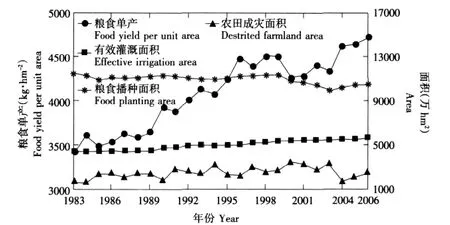
图2 我国粮食单产、粮食播种面积、有效灌溉面积及农田成灾面积变化曲线(1983~2006)Fig.2 Variation curve of Chinese food yield per unit area,food planting area,effective irrigation area and destroyed farmland area from 1983 to 2006

表1 我国粮食总产影响因子变化趋势Table 1 Variation trend of food yield increase influence factors of China
2 我国中长期粮食总产量预测
取我国未来粮食总产量(Y)作为因变量,与我国粮食增产密切相关的粮食单产(X1)、粮食播种面积(X2)、化肥施用量(X3)、有效灌溉面积(X4)、农机总动力(X5)、农田成灾面积(X6)作为自变量,采用EXCEL软件中的数值分析工具进行多元线性回归分析。
2.1 回归方程
根据我国1983~2006年因变量及各自变量数据,采用Excel软件进行回归分析,得到我国粮食总产量数学模型:
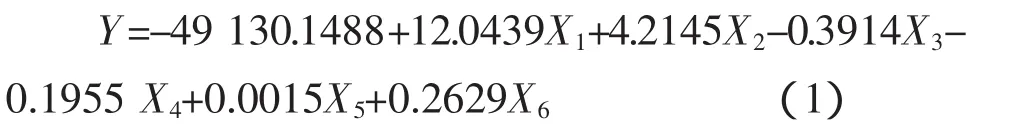
该模型R2=0.9998。
2.2 F检验
对模型进行F检验。F=13 120.74,当α=0.05时,F0.05=2.70,F>F0.05,说明回归效果非常显著。
2.3 t检验
对各回归系数进行t检验,结果见表2。

表2 回归系数t检验结果Table 2 Inspection results of regression coefficient t
2.4 模型调整
采用向前选择变量法对自变量集合进行调整[15]。
首先,计算粮食总产量Y与6个潜在自变量之间的简单相关系数,结果见表3。
选择相关系数最大的X1首先进入模型:Y=7 544.5287+9.0888X1,R2=0.8519
F 检验:F=126.54 ,F0.05(1,22)=4.30,F>F0.05,说明回归效果非常显著。
t 检 验 : t0=2.2711, t1=11.2489,t0.025(22)=2.0739,t0、t1均大于t0.025(22),说明各回归系数估计值通过t检验。
除X1外,还有5个潜在自变量在模型外。现以 X1与 Y为减模型,以 X1、Y与 X2、X3、X4、X5、X6中的任意一个作为全模型,依次进行偏F检验。在通过偏F检验的变量中,选择Fj最大者进入模型,其余依此类推,计算结果见表4。
根据上述变量选择结果,以粮食总产量(Y)作为因变量,粮食单产(X1)、粮食播种面积(X2)、化肥施用量(X3)、农田成灾面积(X6)作为自变量,采用1983~2002年自变量和因变量序列资料(n=20)进行多元线性回归分析,得到最终模型为:
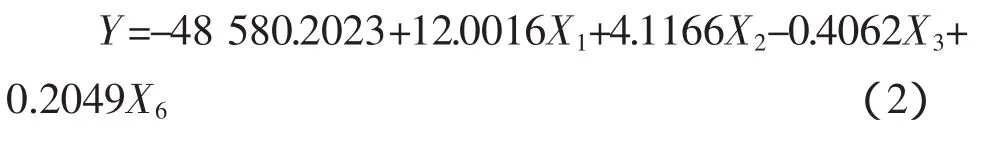

表3 Y与X1~X6的简单相关系数Table 3 Simple related coefficients between Y and independent variables(from X1to X6)

表4 向前选择变量法计算结果Table 4 Calculation results of forward selection variables method
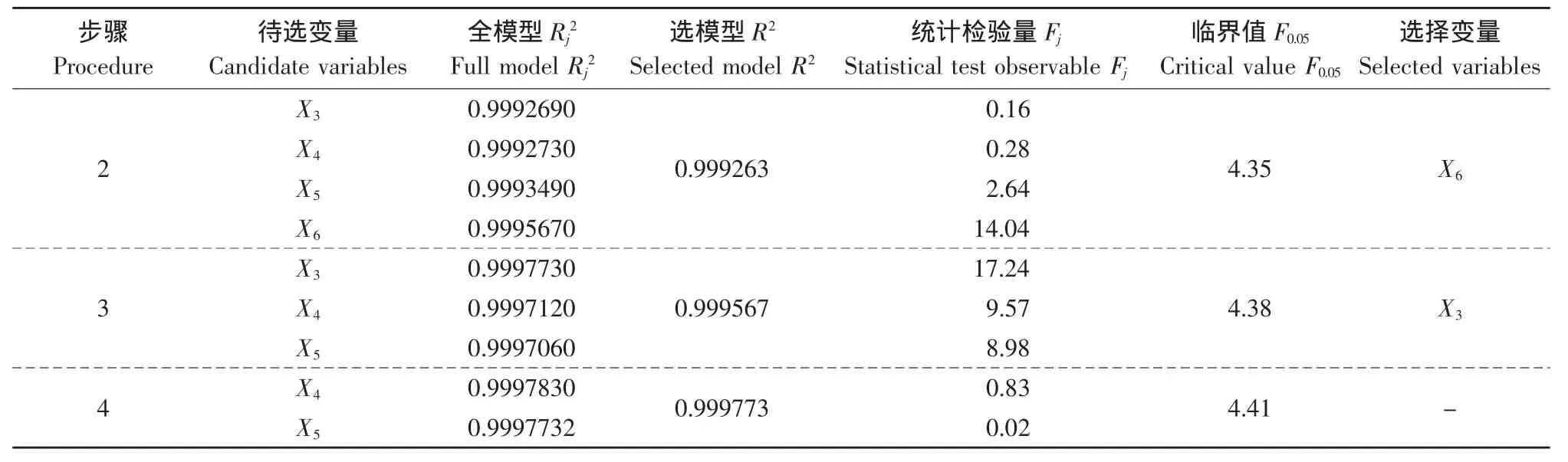
续 表
该模型R2=0.9998。F检验:F=18 363.43,F0.05(4,15)=3.06,F>F0.05,说明回归效果非常显著。t检验:t0=-57.2746,t1=45.9726,t2=50.2722,t3=-3.4242,t4=3.5443,t0.025(15)=2.1315,均大于t0.025(15),说明各回归系数估计值通过t检验。
2.5 回归模型精度检验
采用建立的我国粮食总产量多元线性回归方程对1983~2002年我国粮食总产量进行拟合,见图3。
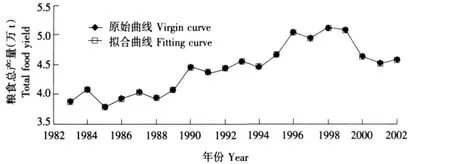
图3 我国粮食总产量拟合曲线(1983~2002)Fig.3 Fitting curve of total food yield of China from 1983 to 2002
经过计算,拟合准确率为100%(相对误差e<20%为合格[13-14])。从图1可以看出,所建粮食总产量多元线性回归模型拟合效果良好。
采用式(2)计算出2003~2006年我国粮食总产量的预测值,然后采用未参加建模的2003~2006年我国粮食总产量的原始数据进行后验预测检验,见表5。
经过计算,预测检验合格率为100%(相对误差e<20%为合格),达到1级标准。因此,所建的我国粮食总产量多元线性回归模型可靠性和预测精度较高,可用于预测我国未来粮食总产量。
2.6 回归模型预测
预测结果见表5。

表5 2003~2006年我国粮食总产量后验预测误差Table 5 Total food yield posterior forecasting error of China from 2003 to 2006
将表1中粮食单产(X1)、粮食播种面积(X2)、化肥施用量(X3)、农田成灾面积(X6)2010年、2020年、2030年的预测值代入式(2),得到2010年、2020年、2030年我国粮食总产量的预测值:
Y2010=50 065 万t,Y2020=60 268 万 t,Y2030=71 613万t
本文预测结果与丁晨芳的预测结果51 369.6万t(2010年)[5]和王海全[15]的预测结果60 267~64 975万t(2020年)、69 351~73 019万t(2030年)[18]基本一致。
3 结 论
a.采用多元线性回归分析方法构建了我国中长期粮食总产量预测模型。经过计算,2007~2010年、2011~2020年、2021~2030年我国粮食总产量年平均增长率分别为0.16%、2.04%、1.88%。计算结果表明,只要措施得当,未来我国完全可以在耕地资源不可逆转减少的前提下实现粮食总产量的持续增长。
b.由上述建模过程可以看出,粮食单产、粮食播种面积、化肥施用量及农田成灾面积是我国粮食总产量的关键制约因素,因此,加大科技投入、提高粮食单产、提高复种指数、扩大粮食种植面积、合理增加化肥施用量以及加强水利投入、控制农田成灾面积实现我国粮食增产的根本措施。
c.需要指出的是,虽然所建多元线性回归模型通过了精度检验,但式(2)中自变量化肥施用量(X3)和农田成灾面积(X6)的回归系数出现了与生活常识相反的符号,对因变量粮食总产量(Y)的解释作用不强,这主要是由于各变量间存在较严重多重相关性所导致的,有待于今后进一步进行研究。
[1]李晓东,席升阳,潘立.基于最小二乘支持向量机的中国粮食产量预测模型研究[J].水土保持研究,2007,14(6):322-324.
[2]尹宗成.运用粗糙集理论对我国粮食产量的预测[J].统计与决策,2008(6):46-48.
[3]贺福利,胡勇,陈淳.用灰色马尔柯夫链预测模型对我国粮食产量的预测[J].数学的实践与认识,2003,33(12):45-47.
[4]Singh R,Ibrahim A E.Use of spectral data in Markov chain model for crop yield forecasting[J].Journal of the Indian Society of Remote Sensing,1996,24(3):145-152.
[5]丁晨芳.组合模型分析方法在我国粮食产量预测中的应用[J].农业现代化研究,2007,28(1):101-103.
[6]Kandala V M,Prajneshu.Fuzzy regression methodology for crop yield forecasting using remotely sensed data[J].Journal of the Indian Society of Remote Sensing,2002,30(4):191-195.
[7]王惠文,孟洁.多元线性回归的预测建模方法[J].北京航空航天大学学报,2007,33(4):500-504.
[8]苗菁,吴小花.聚类回归与多元线性回归的对比研究[J].现代预防医学,2006,33(4):491-493.
[9]罗娅妮,郭永洁.试论多元线性回归模型在股票定价中的运用[J].财会通讯:理财版,2008(9):26-28.
[10]吴宏斌.地下水水质预测的多元线性回归分析模型研究[J].山西建筑,2007,33(32):201-202.
[11]刘晶,王世新,周艺.我国粮食生产主要影响因子的灰色关联动态分析[J].国土与自然资源研究,2007(1):54-55.
[12]付强.数据处理方法及其农业应用[M].北京:科学出版社,2006.
[13]张欣莉,丁晶,金菊良.基于遗传算法的参数投影寻踪回归及其在洪水预报中的应用[J].水利学报,2000(6):45-48.
[14]金双彦,秦毅,李雪梅,等.黄河下游夹河滩站洪水最大含沙量预报研究[J].泥沙研究,2008(2):58-61.
[15]王海全.我国粮食生产增长潜力及激励措施究[J].湖北经济学院学报,2006,4(3):83-89.

