高速磁浮线路道岔钢梁移位过程及其数值分析
张宏君
(上海磁浮交通发展有限公司,201204,上海∥工程师)
1 道岔梁基本结构及几何参数
高速磁浮线路道岔钢梁主体结构截面形式为箱形等截面梁,其主梁截面如图1所示。
道岔主体结构部分钢梁长77.338 m,支承在0~5号共6个支墩上(其中0号支点为固定端)。其等效示意图见图2。轨道切换时,道岔在0号支点固定,位于3、5号支墩处的驱动系统对道岔施加侧向力,道岔钢梁发生弹性变形,使道岔各支点达到系统要求的预定位置(第3点的侧移位移为1.17 m,第5点的侧移位移为3.553 m,其它3个点为从动点),并使整个道岔曲线形状满足系统要求。
道岔切换过程中活动端的变形约为梁长度的1/20,变形较大,故道岔切换过程需采用大变形分析;整个过程分多步模拟,提供支点移动过程、道岔变形过程、驱动力要求,以及相应内力、支反力等关键数据。
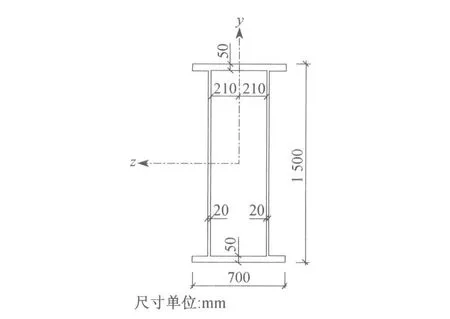
图1 道岔钢梁主截面图
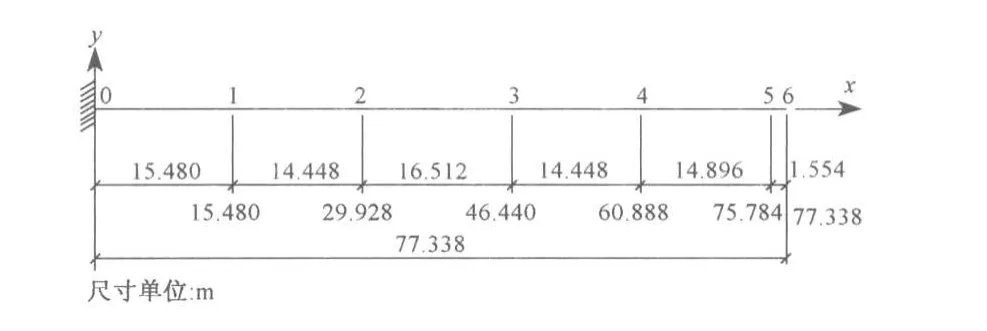
图2 道岔钢梁等效示意图
2 梁的移位方式及变形特性
2.1 梁的移位方式
道岔移位时,支点3、5通过驱动电机向道岔提供驱动力,0支点固定,1、2、4支点随动,各活动支点分别沿其导轨移动,在导轨端部设有限位。道岔的曲线形式由行车要求确定,与梁的弹性变形曲线不完全一致。由于只有两个主动力可以调整,理论上讲,道岔梁在这两个力的作用下发生弹性变形,即使这两个力可正可负,能任意组合,也只可保证两点的位置,无法直接达到行车要求的位置;故需借助插销或限位提供的反力调整曲线形状,满足车辆行驶要求。
2.2 道岔钢梁的弯曲特征
弯曲道岔的形成基于以下边界条件:
·有利于列车的平稳运行;
·保证乘客足够舒适度;
·车辆运行过程中惯性力分布利于弹性弯曲道岔钢梁的内力及疲劳强度。
从以上条件出发,考虑钢梁弯曲状态曲率半径变化规律,道岔曲线部分宜采用5段分段函数,即直线——缓和曲线——圆曲线——缓和曲线——直线。道岔变形曲线如图3所示。
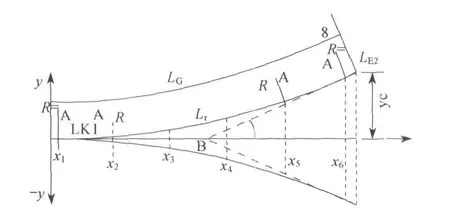
图3 道岔变形曲线
3 道岔钢梁切换过程的力学分析
道岔切换过程,即为道岔钢梁在两个驱动电机驱动下发生弹性变形,使5个支承点达到系统要求的位置的过程。
切换方案的基本过程为:位于支点3和支点5的两个驱动电机均匀同步地行进,驱动力逐步增加,支点1、2、3逐个到位;支点3到位后,位于支点5的电机继续前进,使支点4、5逐个到位;然后5个支点同时插销,电机断电停机,道岔切换完成。
为保证道岔侧线曲线段与直线段平滑连接,道岔固定端以刚接为宜。本计算分析中假定其为固定点刚接。根据实际采用的道岔固定端的节点构造形式,节点基本可实现抗弯约束,但也可能发生微小转动,因此本文除对固定端按刚接计算外,也对部分状态按铰接假定进行了分析,以便为道岔设计提供全面的参考依据。
3.1 加载方式
整个驱动过程大致均匀地分为若干步。根据初步分析数据,以驱动点5为主要参照点,以该点每移动约0.15~0.16 m为一步,全程分23步。各步加载的位移见表1。表中给出支点3、5两个驱动点各步的位移,3个从动点的位移由计算确定。其中第7、17、20、22、23步分别使 1~ 5支点到达其最终位置。

表1 切换过程中加载的位移m
3.2 固定端刚接梁模型分析
使用 ANSYS软件进行数值模拟计算,选择BEAM 4梁单元进行计算,采用大变形分析方法。
3.2.1 切换过程的驱动力和随动点限位支承反力变化
道岔梁切换过程中两个电机驱动力及20步以后支点3电机的被动力变化过程见图4、图5。至第20步驱动点3到位,此后该电机位置保持,该点的力变为被动力。
3.2.2 切换到位后道岔钢梁的曲线
经上述驱动过程,道岔达到其侧道弯曲位置。转角和曲率半径沿纵向x的变化见图6、图7。
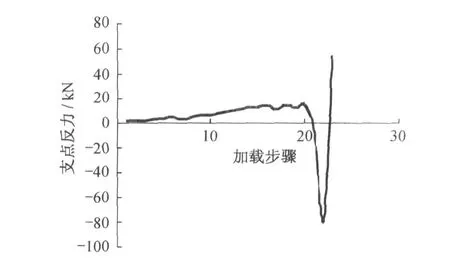
图4 支点3反力变化
3.3 固定端铰接梁模型分析
为与刚接模型比较,把固定端换为铰接进行计算分析,列出关键步骤数据。
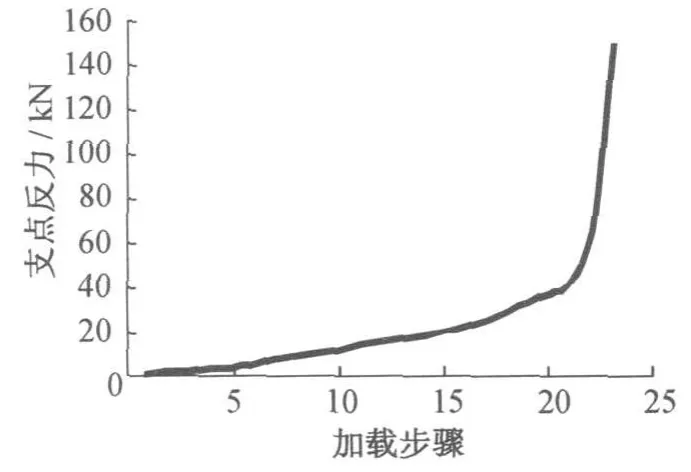
图5 支点5反力变化
驱动过程中5个支点到位时各关键点相应的位移和转角见表2,相应驱动力和支点反力见表3。驱动过程中5个支点到位时梁的变形曲线见图8。
从铰接模型驱动力和反力的数据看,其与刚接模型相差不大,说明即使固定端不能实现绝对刚接,对驱动电机的选型和限位设计的影响也不大。从位移数据看,固定端刚接和铰接的曲线形式影响不大,两端转角略有不同。固定端刚接时无转角,而铰接时将产生0.000 25 rad的转角。这个数值是比较小的。铰接自由端转角为0.097 1 rad,与刚接时几乎无差别,说明固定端接点刚度只影响接点附近,距离固定点越远受影响越小,对自由端几乎无影响。

图6 转角沿纵向变化
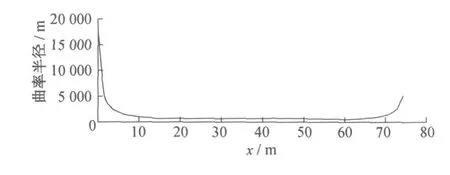
图7 曲率半径沿纵向变化

表2 铰接模型切换过程中各点的位移变化

表3 铰接模型切换过程中主动力与各点的反力变化 k N
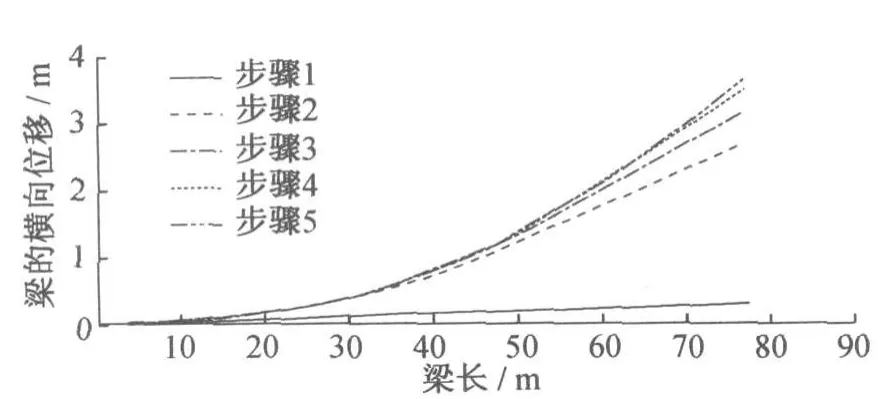
图8 铰接模型变形曲线
3.4 固定端刚接壳模型及与梁模型的比较
使用ANSYS软件进行数值模拟计算,采用梁模型(BEAM4)、壳模型(SHELL63)两种单元分别进行计算,采用大变形分析方法。
为保证数据的可靠性,采用更精确的壳单元模型对切换过程中的5个关键步(分别对应5个支点到位时的状态)进行了校验。计算中认为固定点刚接,采用与梁单元模型同样的位移加载制度(见表4)。

表4 切换过程位移加载制度 m
3.4.1 切换过程驱动点和从动点的轨迹比较
切换过程中各点的位移变化比较见表5。
3.4.2 切换过程的驱动力和随动点限位支承反力变化比较
两种模型切换过程的驱动力和从动点限位支承反力见表6。
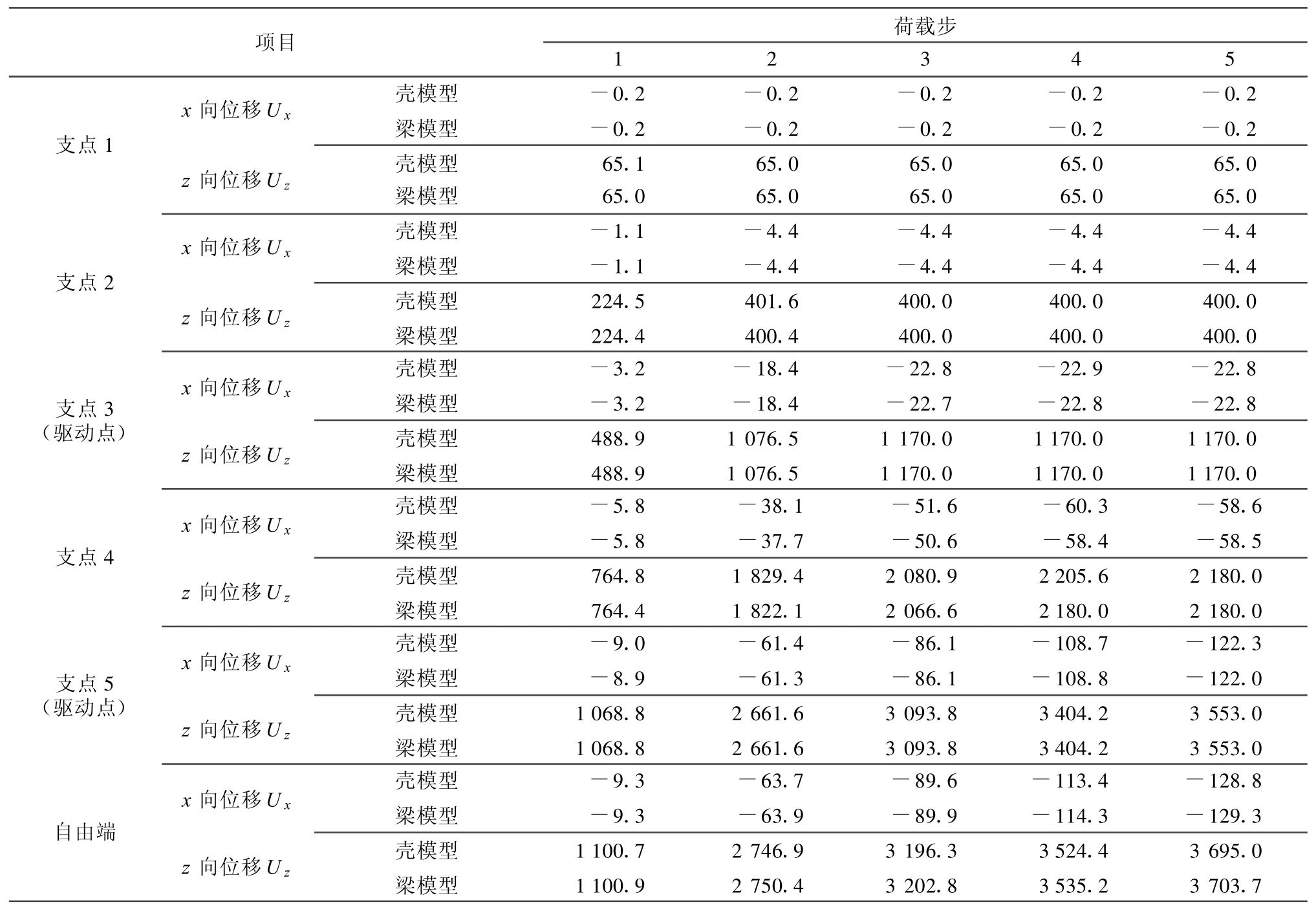
表5 切换过程中各点的位移变化比较mm
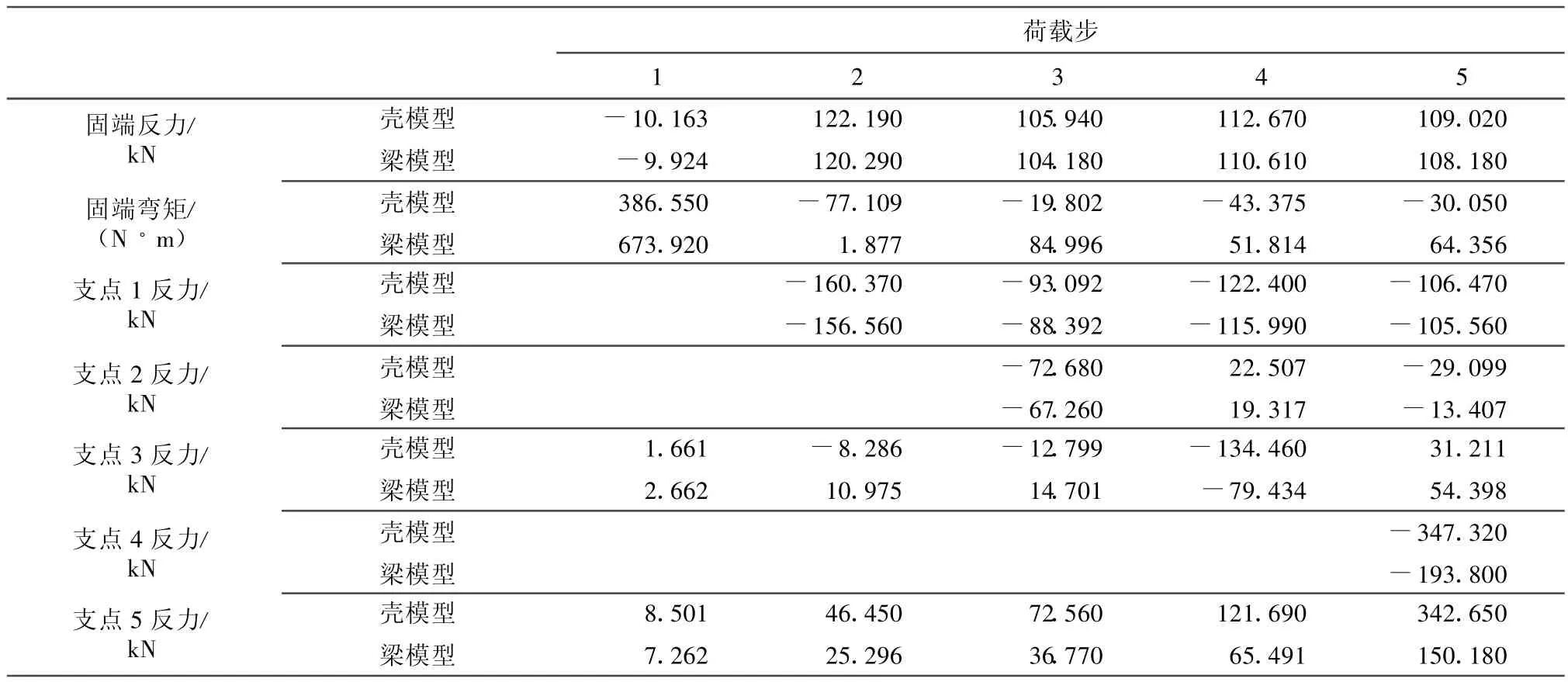
表6 切换过程中主动力与各点反力变化比较
3.4.3 切换到位后道岔梁的曲线比较
两种模型下切换到位后道岔的侧向位移、纵向位移和转角比较如图9~11所示。

图9 两种模型下切换到位后道岔梁的x坐标分布比较图

图10 两种模型下切换到位后道岔梁的z坐标分布比较图

图11 两种模型下切换到位后道岔梁的转角分布比较图
从两种模型计算出的内力和变形数据比较情况看,吻合得还是非常好的,证明了梁单元模型的分析数据是相当可靠的。
4 结语
从固定端铰接模型与刚接模型驱动力和反力的数据看,两者相差不大,说明即使固定端不能实现绝对刚接,对驱动电机的选型和限位设计的影响也不大。从两种模型的位移数据看,曲线形式影响不大,说明固定端接点刚度只影响接点附近,距离固定点越远受影响越小,对自由端几乎无影响。
从BEAM4、SHELL63两种单元模型计算出的内力和变形数据比较结果看,两组数据相当吻合。因此,在进行计算时,如果不要求得到截面上的细部结果,可用梁模型进行计算,这样既快速又节省磁盘空间;如果要得到截面上的一些细部结果,由于梁模型不能反映细部的情况,就必须采用壳模型进行计算,以获取相应的数据。
[1]刘华清,李志业,任恩恩,等(编译).德国磁浮列车Transrapid[M].成都:电子科技大学出版社,1995.
[2]殷宁骏.磁浮线路[J].铁路建筑,1996(8):23.
[3]王国强.实用工程数值模拟技术及其在ANSYS上的实践[M].西安:西北工业大学出版社,2001.
[4]翁秀玲.磁浮线路轨道梁技术方案和特点[J].城市轨道交通研究,2008(4):28.
[5]徐芝纶.弹性力学[M].北京:高等教育出版社,1982.

