城轨列车特性曲线计算系统的实现及应用
骆礼伦
(中铁第四勘察设计院集团有限公司,430063,武汉∥助理工程师)
目前,我国在进行城市轨道交通列车牵引计算时,一般参照铁路列车的牵引计算规程和国外的城市轨道交通牵引计算方法。鉴于此,有必要开发有自主知识产权的城轨列车特性曲线计算系统,为城市轨道交通系统设计提供重要依据和参数。
1 列车牵引制动特性计算数学模型
由于列车行驶过程中受力变化很复杂,因素间的影响具有多重性和非线性,为此对列车的受力分析进行线性简化,认为列车运行在平直轨道上,在足够短的时间内进行匀加速运动。可根据牛顿第二运动定律,分析出列车受力情况和运行规律。城轨车辆牵引制动特性计算相关数学模型包括牵引力、起动阻力、基本阻力、制动力、列车运行过程等。
1.1 牵引力计算
牵引力计算模型是根据电机运行特性建立的,在不同的列车速度区间具有不同的数学模型。
在恒力区时,
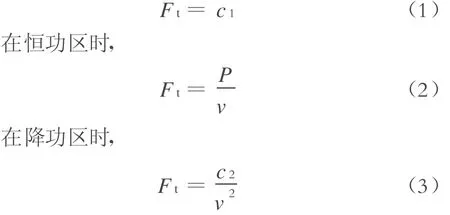
式中:
Ft——牵引力 ;
c1——常数;
P——恒功区轮周功率;
v——速度;
c2——常数,其值为恒功区轮周功率与降功点速度的乘积。
1.2 起动阻力计算
起动阻力的速度范围,一般界定在0~5 km/h,其经验公式为:

式中:
fs——单位起动阻力,N/k N;
fu——零速度时单位起动阻力,N/k N;
v0——起动阻力消失点速度,m/s。
1.3 基本阻力计算
基本阻力的计算是一个非常复杂的过程,为简化起见,一般采用大量试验总结的经验公式。单位基本阻力的计算公式一般形式为:

式中:
wo——单位基本阻力,N/k N;
b1、b2、b3——常数,其值由试验总结确定。
1.4 制动力计算
列车制动力是由制动装置产生的与列车运动方向相反的外力,是人为的和可控的。制动力和列车运行阻力都阻止列车的运动。列车制动过程受到的阻力是制动力、运行阻力之和。
1.5 列车运行过程数学模型
1.5.1 加速度计算模型
(1)牵引过程的加速度:
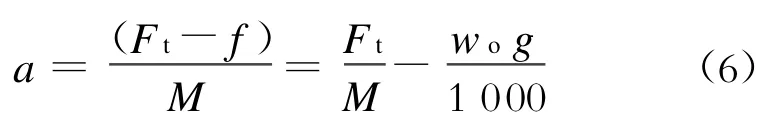
式中:
a——列车运行加速度,m/s2;
f——列车运行总阻力,N;
M——列车总质量,kg;
g——重力加速度,取9.8 m/s2。
(2)制动过程的加速度:

式中:
c3——列车制动加速度,其值为常数。
1.5.2 运行速度数学模型

式中:
v2——本步长终点速度;
v1——上一步长终点速度;t——时间步长。
1.5.3 运行距离数学模型
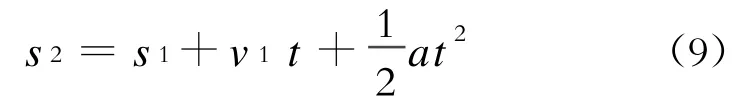
式中:
s2——本步长列车运行距离;
s1——上一步长列车运行距离。
2 系统主要模块的实现
系统采用0.03 s作为一个迭代步长。系统首先运行牵引模块,每迭代一次就进行一次制动判断,如果满足制动要求,运行制动模块。制动模块的迭代过程和牵引模块相似,故本文只介绍牵引模块迭代过程。
牵引模块算法如下:
步骤1:初始化迭代步长、速度、加速度、区间长度、列车参数等。
步骤2:如果第一次进行迭代,速度、运行距离为零;反之,根据上一次迭代的速度、加速度、运行距离计算此次迭代的速度、运行距离;如果计算的速度大于最高速度时,需修正此次迭代步长。
步骤3:根据步骤2计算的结果,运用基本阻力公式计算列车运行阻力。
步骤4:根据步骤2计算的速度值,判断速度小于起动阻力消失点速度,则比较起动阻力与基本阻力大小,取大值作为运行阻力值;反之,取基本阻力值为运行阻力值。
步骤5:根据步骤2计算的速度值,判断牵引状态属于区域(恒力区、恒功区、降功区等),并计算对应牵引力。
步骤6:根据步骤4和步骤5的计算结果,计算列车加速度值。
步骤7:根据列车停车精度要求,采用线性插值法判断列车是否达到制动要求。如果没有达到制动要求,系统转到步骤2;反之,牵引模块结束,系统进入制动模块。
3 系统实现的技术路线
以普通PC机为系统硬件,以MATLAB编程技术为基础,针对用户的实际需要和城市轨道交通列车运行的特点,综合数值分析、数据处理等相关技术开发本系统。图1为系统的内部组成结构。该系统体系结构共包括五层。当系统运行时,底层的模块能实时地为上层模块服务,同一层的模块间有信息传递。
第一层为基础层。该层由MATLAB编程平台和Excel数据库软件构成,为整个仿真系统提供最基本的软件支持。
第二层为信息载体层。输入参数文件由Excel数据库软件制作而成。输入参数检查模块能更好地服务和辅助用户使用该系统。牵引模块接收来自界面或输入参数文件的参数并分析计算,把计算结果传递给制动模块。制动模块仿真列车制动过程。
第三层为动态模块层。牵引制动计算模块直接面向用户并为上层模块服务。计算结果文件是保存分析结果的载体。
第四层为交互层。参数输入模块是控制输入参数的界面,在输入参数检查模块的支持下,可以很好地辅助用户完成输入操作。绘图模块把牵引制动计算模块的分析结果以图形的方式表现出来。参数输出模块完成计算结果的保存。
第五层为系统高级界面。该界面是用户直接面对和操作的界面,它将可操作的相互联系、彼此服务的各功能模块提供给用户。
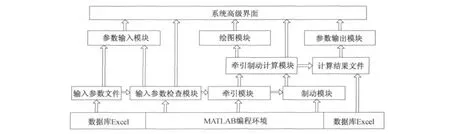
图1 系统体系结构
4 实例分析
实例计算参数:列车编组为2动2拖;动车自重35 t,载客量为250人;拖车自重29 t,载客量为230人;列车(0~36 km/h)的平均起动加速度为0.83 m/s2,制动加速度为1.0m/s2;列车最高运行速度80km/h。运用列车特性曲线计算系统获得的列车牵引力、阻力特性曲线,以及列车制动力、阻力特性曲线如图2、图3所示。图2和图3的输出结果进行了单位转换。
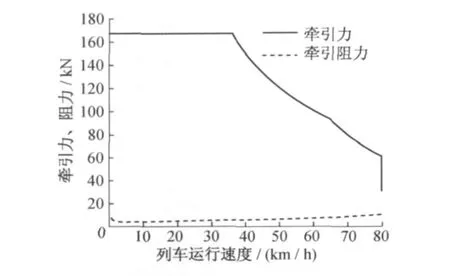
图2 列车牵引力、阻力特性曲线

图3 列车制动力、阻力特性曲线
5 结语
城市轨道交通列车的牵引、制动计算过程是一个复杂的、非线性的过程。本文依托经验公式建立了城市轨道交通列车牵引、制动计算的单质点模型,并借助MATLAB软件对列车在平直轨道上的牵引和制动过程进行模拟研究,较好地实现了列车牵引和制动特性曲线的模拟。目前,该系统已经在武汉、郑州、苏州、无锡、昆明等城市的轨道交通工程设计中得到应用。实践证明,本系统对城市轨道交通系统的设计具有很好的指导意义。
[1]TB/T 1407—1998 列车牵引计算规程[S].
[2]王午生,许玉德,郑其昌.铁道与城市轨道交通工程[M].上海:同济大学出版社,2003.
[3]孙章,何宗华.城市轨道交通概论[M].北京:中国铁道出版社,2000.
[4]徐安.城市轨道交通电力牵引[M].北京:中国铁道出版社,2000.
[5]孙中央.列车牵引计算规程实用教程[M].北京:中国铁道出版社,1999.
[6]彭其渊,石红国,魏德勇.城市轨道交通列车牵引计算[M].成都:西南交通大学出版社,2005.

