主动移相式孤岛检测的一种改进的算法

刘芙蓉 康 勇 王 辉 段善旭 唐爱红

（1. 武汉理工大学自动化学院 武汉 430070 2. 华中科技大学电气与电子工程学院 武汉 430074）

1 引言

孤岛检测是并网光伏（PV）系统及其他分布式发电系统必备的功能，指在公共电网失压后，光伏系统能及时检测出失压状态并作处理，避免非计划性孤岛引起的人身或设备损失。

过（欠）电压保护和高（低）频保护能有效减少非计划性孤岛，但在光伏系统发出的有功、无功恰好与本地负载消耗的有功、无功相当时，失压前后频率、电压没有明显变化，被动式孤岛检测失效，要依靠主动式孤岛检测才能辨识孤岛，即要对光伏并网逆变器的输出施加扰动，使电压或频率偏离正常范围，实现孤岛保护。

并网光伏逆变器采用电流控制模式与公共电网相连，控制量为逆变器输出电流，对输出电流的扰动可加在幅值、频率或相位上。现在公认为有效的方法有：针对幅值施加扰动的电压正反馈法[1]、有功功率扰动法[2]，针对频率施加扰动的主动移频法[3-5]，针对相位施加扰动的无功功率扰动法[6]、主动移相法[7-8]等。这些方法都能通过软件实现并取得较好的效果，但如果技术处理不好，会加重DSP的运算负担，或导致孤岛检测性能不达标[9]、或使输出电能质量畸变率增大等。

主动移相式孤岛检测方法对相位θ 施加扰动来实现孤岛检测，具有检测能力强、电流畸变小、适用于多光伏系统等优点。文献[7-8]提出的滑模频率偏移法（Slip-Mode Frequency Shift，SMS）和文献[10-11]提出的自动移相法（Automatic Phase Shift，APS）为主动移相式孤岛检测算法的典型代表，它们能有效地检测出孤岛状态，但算法及判断逻辑较复杂，增大了DSP实现的难度。本文提出一种改进算法，能简化DSP的实现，且对电能质量不良影响小，检测能力完全满足孤岛检测的标准[9,12]要求。

2 主动移相式孤岛检测的常用算法

对光伏逆变器的输出电流进行控制时，电流给定信号是按周期给出的（见图1）：取上一周期公共点电压的频率（锁相环PLL测得）作为本周期电流的频率，周期的起始时刻为公共点电压的过零上升时刻，初始相位由主动移相算法计算得出。

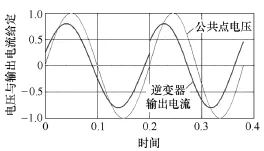
图1 SMS孤岛检测方法示意图Fig.1 Illustration of SMS method

最早出现的主动移相算法称为 SMS算法[7-8]，它对初始相位角的计算公式为

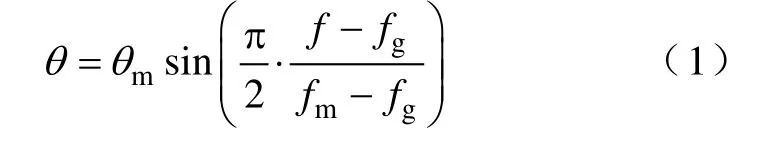
式中，θm为移相算法设置的最大相移角；fm为最大相移发生时的对应频率；fg为电网额定频率；f为测得的公共点频率。

在其后出现的主动移相算法APS中[10]，初始相位角按下式计算。

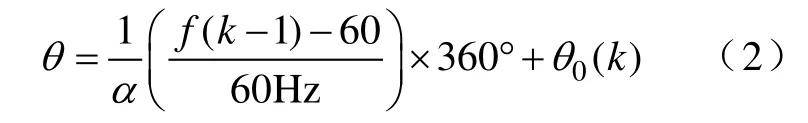
为解决APS算法中“孤岛稳态”的判断问题，文献[11]提出了“自适应逻辑移相算法（ALPS）”，通过前N个周期的频率变化趋势统计来判别附加小量∆θ 的引入与否。该方法实施相对容易，但其依据的判断逻辑不适用于所有容性负载，容性负载下该判断逻辑可能使附加小偏置的功能失效，产生θ0(k)=0而起不到增强扰动、减小盲区的作用。

3 新算法的提出

由于实际电网及负载参数的变化有一定范围，使移相算法的设计及参数整定有了限定依据，只要移相算法能满足实际负载涵盖的负载群的孤岛检测要求，就是有效的孤岛检测算法。电网中的实际负载在孤岛检测中的效应可以用 RLC并联谐振负载来等效[2]，它也是孤岛检测测试标准[9]中采用的测试负载。为更好地讨论孤岛检测与负载特性间的关系，对负载参数重新定义如下[14]：

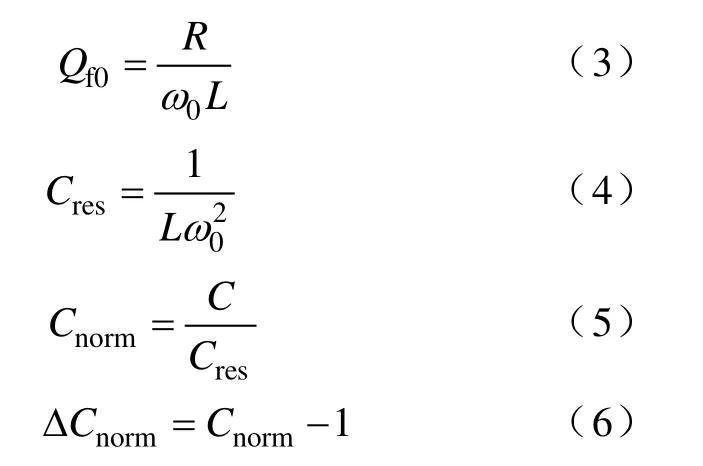
式中，R、L、C分别为RLC并联谐振负载的电阻、电感、电容值；ω0为电网角频率（额定值）；这里Qf0有别于负载品质因数，但当负载谐振频率与电网频率相等时，两者大小相等。

本文提出的新算法可以表示为

式中，k为主动移相算法的反馈系数。

比较式（1）、式（2）、式（7），可知新算法比式（1）简洁、又省掉了式（2）算法繁琐的稳态判断和附加小量θ0(k)。下文将说明，只要反馈系数 k选择合理，式（7）算法完全可以满足孤岛检测技术标准[9]的要求。

4 新算法的参数整定

从 PV逆变器的电流控制通道看，电流与公共点电压的相位差受孤岛检测算法（即主动移相角θ）和RLC负载相位角 ∠ G (jω)的影响，如图2所示。当θ+∠G (jω)＞0时，PLL检测到的新电压周期将变短，导致下一周期电流给定频率增加，使公共点电压的频率有增大趋势；当θ+∠G (jω)＜0时，PLL检测到的新电压周期将变长，会降低给定电流的频率，使公共点频率有减小趋势。因此，要使电网断开后公共点频率偏离电网频率，只要满足

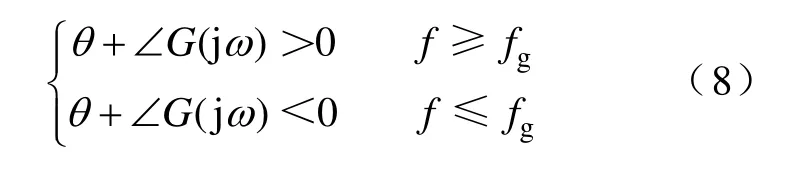
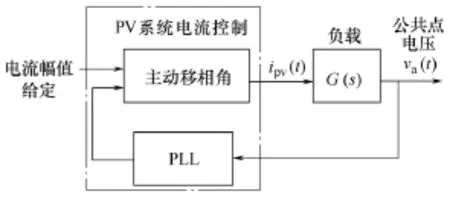
图2 PV系统的等效模型Fig.2 Control scheme of PV system

如果上述关系保持不变，频率将被单向推高（或降低），直到超出正常范围，孤岛便能被检测。

图3为断网后主动移相算法成功检测孤岛的示意图，其中曲线1、2、3为负载的相位角/频率特性曲线，分别代表额定电网频率下呈阻性、感性和容性的RLC负载，曲线4为移相算法θ = 0.2∆f的移相角/频率曲线，曲线5、6、7为三类负载的(j)Gθω+∠频率特性曲线（由于讨论的频率变化范围较小，特性曲线看起来像一组平行直线）。当(j)Gθω+∠位于坐标水平轴线上方时，有(j)Gθω+∠＞0，公共点频率在电流控制作用下有增大的趋势；(j)Gθω+∠位于水平轴线下方时，公共点频率有变小的趋势。

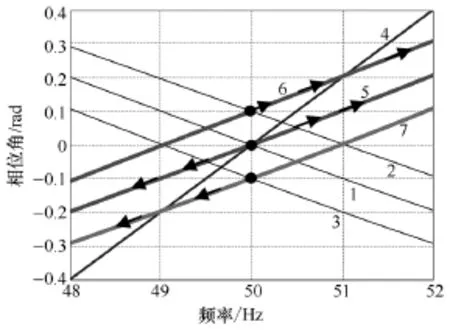
图3 谐振负载电容值发生变化时负载相位角随频率变化的情况以及电网失压后公共点频率变化轨迹Fig.3 Phase vs. frequency behavior of parallel RLC loads,and frequency deviation locus after grid is disconnected

因此，电网失压后频率变化如下：

（1）如谐振负载并网时呈阻性，如曲线1，则频率在扰动下将向上或向下偏离原值，如曲线5箭头所示。

（2）如果谐振负载在电网频率下呈感性，如曲线2，电网失压时θ+∠G(jω)＞0，公共点频率将单向变大，轨迹如曲线6箭头所示。

（3）如果谐振负载在电网频率下呈容性，如负载曲线3，电网失压时θ+∠G(jω)＜0，公共点频率将单向变小，轨迹如曲线7。

综上分析，孤岛检测成功的充分条件是θ+∠G(jω)穿越水平轴时切线斜率大于零，即

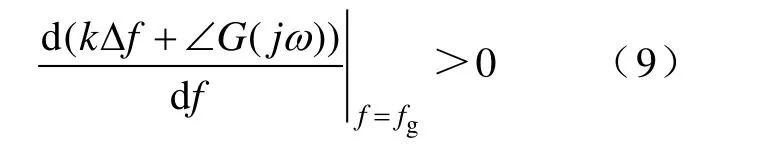
其中

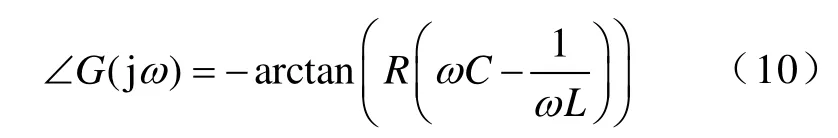
将式（3）～式（6）代入式（9），得

式（11）为主动移相算法（式（7））的正反馈系数k与孤岛检测能力间的关系，将几组不同参数代入得到下表。

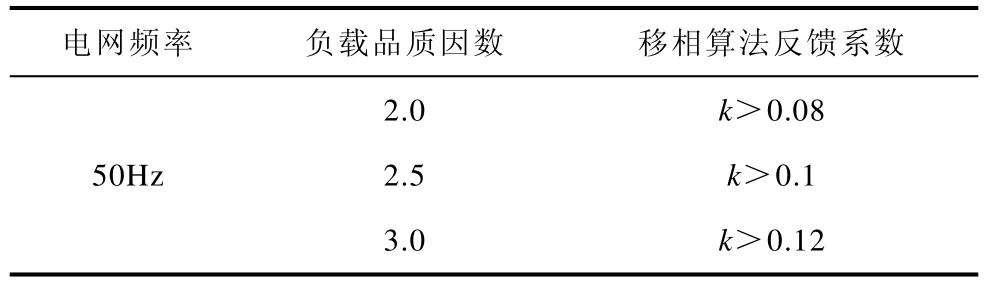
表 不同负载下孤岛检测成功的条件Tab. Boundary condition of a successful detection

5 θ =k·∆ f算法对电能质量的影响

相邻周期间的相位差是造成电流畸变的主要因素，而相位差与频率偏差成正比。公共点频率对电网频率的偏差信号包含：①偏差信号的直流分量；②偏差信号的交流分量。

频率偏差信号的直流分量不会引起 PV输出电流畸变，因为它对初始相位的影响在每个周期都相同，使电流波形前后相连为连续的正弦波，这也是主动移相式孤岛检测方法比主动移频式孤岛检测方法优越的地方。对频率偏差信号的交流分量引起的输出电流畸变，可通过减小移相算法的反馈系数 k来降低其影响，但降低k后孤岛检测能力随之降低，按式（11）进行参数整定，可以在满足孤岛检测性能要求的情况下，最大限度地减小算法引起的电流畸变率。

下面对算法θ =0.1∆f产生的电流畸变按不利情况进行粗略估算：若电网相邻周期的频率偏差为0.2Hz，将导致逆变器输出电流相邻周期的相位差为0.1×0.2=0.02rad，占整个周期的比例为 0.02/2π=0.0032，引起的总谐波畸变约为 0.3%，几乎可以忽略不计。

6 验证

本文对新算法进行了仿真和实验研究，采用Matlab/Simulink对 3kW 用户用光伏发电系统进行建模，模型中逆变器采用恒电流控制模式，逆变器输出的电能通过 LC滤波后送给负载，并与电网相连。负载采用与逆变器输出功率相平衡的品质因数为2.5的RLC并联负载，电网在0.06s后自动断开。仿真中采用的电网电压为 220V(RMS)，电网频率50Hz。

图4为采用孤岛检测算法θ = 0.1∆f时电网失压后频率偏移情况，它处于检测成功的临界状态，频率虽可被推至下限，但不满足标准中“失压后 2s内检测出孤岛[9]”的要求。图 5为采用孤岛检测算法θ =0.11∆f时电网失压后频率偏移情况，公共点频率在0.8s内被推至频率下限，孤岛能被顺利检出。该组仿真证实了对品质因数为 2.5的 RLC谐振负载，孤岛检测算法中正反馈系数应大于 0.1才能满足检测要求。

图4 孤岛检测算法为θ =0.1∆f，负载Qf=2.5Fig.4 Simulation of frequency deviation after grid is disconnected: θ =0.1∆f, Qf=2.5

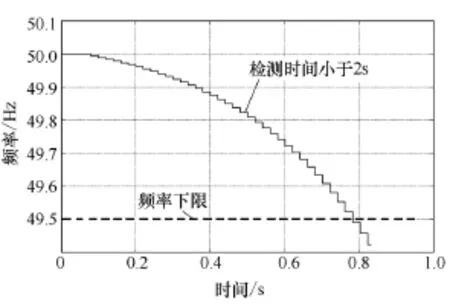
图5 孤岛检测算法为θ =0.11∆f，负载 Qf=2.5Fig.5 Simulation of frequency deviation after grid is disconnected: θ =0.11∆f, Qf=2.5

为进一步验证本文观点，作者利用实验室现有台架（3kW单相逆变器）进行了孤岛实验，实验中采用品质因数约为2的RLC并联谐振负载（谐振频率通过可变电抗器调至50Hz），图6和图7为录下的相关波形。图6为采用θ =0.07∆f时断网前后公共点的电压和频率波形，断网后公共点频率略作偏移即达到稳态，孤岛状况不能有效检出。图7为算法采用θ =0.09∆f时的情况，失压后公共点频率增加，孤岛状况在0.6s内被顺利检出。该组实验验证了品质因数为2的负载，主动移相算法的反馈系数应大于0.08，结果与表一致。

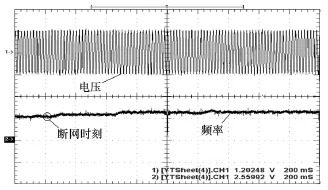
图6 孤岛检测算法采用θ =0.07∆f、负载Qf=2时，电网失压前后公共点的电压和频率Fig.6 Experimental results of IDM with θ =0.07∆f and Qf=2

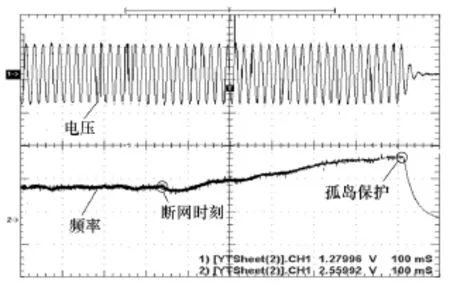
图7 孤岛检测算法采用θ =0.09∆f、负载Qf=2时，电网失压前后公共点的电压和频率Fig.7 Experimental results of IDM with θ =0.09∆f and Qf=2

7 结语

本文对现有主动移相式孤岛检测算法提出了一种改进算法，并对该算法的有效性和参数设置准则进行了讨论，仿真和实验验证了新算法及参数设置准则的有效性。新算法在DSP实现上算法简单，有较好的工程应用价值。

[1]Stevens J, Ginn J, Gonzalez S, et al. Development and testing of an approach to anti-islanding in utilityinterconnected photovoltaic systems[R]. Aug. 2000,Sandia National Laboratories: Albuquerque, NM.

[2]张纯江, 郭忠南, 孟慧英, 等. 主动电流扰动法在并网发电系统孤岛检测中的应用[J]. 电工技术学报,2007, 22(7): 176-179.Zhang Chunjiang, Guo Zhongnan, Meng Huiying, et al. Active current disturbing method for islanding detection of grid-connected inverters[J]. Transactions of China Electrotechnical Society, 2007, 22(7):176-179.

[3]Ropp M E, Begovic M, Rohatgi A. Analysis and performance assessment of the active frequency drift method of islanding prevention[J]. IEEE Transactions on Energy Conversion, 1999, 14(3): 810-816.

[4]郑诗程, 丁明, 苏建徽, 等. 光伏发电系统及其孤岛效应的仿真与实验研究[J]. 系统仿真学报, 2005,17(12): 3085-3088.Zheng Shicheng, Ding Ming, Su Jianhui, et al.Simulation and experiment research of photovoltaic generation system and its islanding[J]. Journal of System Simulation, 2005, 17(12): 3085-3088.

[5]陈卫民, 陈国呈, 吴春华, 等. 基于分布式并网发电的新型孤岛检测研究[J]. 电工技术学报, 2007,22(8): 114-118.Chen Weimin, Chen Guocheng, Wu Chunhua, et al,Research on a novel islanding detection based on grid-connected distributed generations[J]. Transactions of China Electrotechnical Society, 2007, 22(8):114-118.

[6]禹华军, 潘俊民. 并网发电逆变系统孤岛检测新方法的研究[J]. 电力系统及其自动化学报, 2005,17(5): 55-59.Yu Huajun, Pan Junmin.Study on new islanding detecting method for grid-connected power system[J].Proceeding of the CSU-EPSA, 2005, 17(5): 55-59.

[7]Smith G A, Onions P A, Infield D G. Predicting islanding operation of grid connected PV inverters[J].IEE Proc Electr. Power Appl., 2000, 147(1): 1-6.

[8]Ropp M. Design issues for grid-connected photovoltaic systems[D]. Atlanta: Georgia Institute of Technology, 1998.

[9]IEEE Std. 929—2000, IEEE Recommended Practice for Utility Interface of Photovoltaic (PV)Systems [S].Institute of Electrical and Electronic Engineers, New York, Editor. 2000.

[10]Hung G K, Chang C C, Chen C L. Automatic phasephotovoltaic inverters[J]. IEEE Transactions on Energy Conversion, 2003, 18(1): 169-173.

[11]Yin J, Chang L, Diduch C. A new adaptive logic phase-shift alogrithm for anti-islanding protections in inverter-based DG systems[C]. IEEE 36th Power Electronics Specialists Conference, 2005: 2482-2486.

[12]中国国家标准化管理委员会. GB/T 19939—2005光伏系统并网技术要求[S]. 北京: 中国标准出版社,2005.

[13]郭小强, 赵清林, 邬伟扬. 光伏并网发电系统孤岛检测技术[J]. 电工技术学报, 2007, 22(4): 157-162.Guo Xiaoqiang, Zhao Qinglin, Wu Weiyang.Islanding detection method for photovoltaic grid-connected power system[J]. Transactions of China Electrotechnical Society, 2007, 22(4): 157-162.

[14]Liu Furong，Kang Yong, Duan Shanxu. Analysis and optimization of active frequency drift islanding detection method[C]. Proceeding on APEC, 2007:1379-1384.