基于ART神经网络的FCM聚类多目标跟踪方法

李 乐,嵇成新,王春雨

(海军大连舰艇学院,大连 116018)

1 问题的提出

当雷达跟踪空间目标时,往往接收到热噪声、虚警、背景杂波以及其他目标引起的回波,这些非目标回波使估计器进行错误的更新,估计器性能由此大大下降,有时甚至发生目标丢失现象。同时,多部雷达同时监视某一空域,在空域出现多批目标时,由于通信延迟、雷达天线扫描周期不同等原因,在某一时刻,融合中心接收到多部雷达的测量数据构成的空中态势呈现出团状,源于同一目标的测量不可能重合等特点,因此出现了各种数据关联技术。随着模糊理论处理技术和神经网络技术研究的不断深入,将模糊技术与神经网络技术进行有机结合,应该说可以同时发挥以下优势:模糊理论的逻辑推理能力,容易进行高阶的信息处理优势,神经网络技术学习和自动模式识别,并且弥补各自的不足,这是对两者结合的目标跟踪算法进行深入研究的一种必然趋势。

近年来,人们将应用模式识别理论中模糊和聚类理论运用于数据关联的研究,其中基于模糊均值聚类的模糊C均值(FCM)算法研究比较广泛。FCM算法是利用模糊均值聚类的原理,计算量测与航迹之间的隶属阵,根据最大隶属度确定量测与航迹的关联关系。FCM算法的性能强烈地依赖类中心的初始化,但其初始类中心又是随机选取的。如果能选择与实际类中心近似的初始类中心,将减少算法的迭代次数,缩减聚类时间,并很快收敛于实际的类中心。

2 FCM算法

在众多的模糊聚类算法中,应用最广泛且较成功的是1974年由Dunn提出并由Bezdek加以推广的FCM算法。FCM算法是把n个数据Xi(i=1,2,…,n)分成c个模糊簇,并求得每个簇的类中心,使目标函数达到最小。同时,FCM算法通过优化模糊目标函数得到每个样本点相对类中心的隶属度,自动对数据样本进行分类,从而决定样本点的分类。FCM算法的目标函数为:

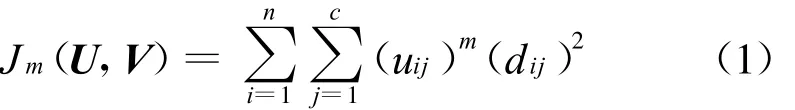
为使Jm最小,类中心和隶属度更新如下:

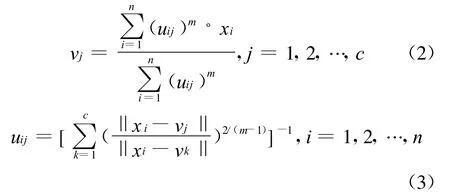
当dij=0时,则 uij=1,uik=0,k≠j,i=1,2,…,n。

但其有一些自身的缺点:

(1)聚类的类数不能自动确定,使用时必须确定聚类的有效性准则;

(2)类中心的位置和特性不一定事先知道,必须由随机初始化产生;

(3)对大数据集进行聚类时,运算开销太大;

(4)在很多情况下,算法对噪音数据比较敏感。

3 ART神经网络

3.1 ART神经网络理论

神经网络理论中的自适应谐振理论(ART)是由美国Boston大学的A.Grossberg和A.Carpentet提出的。ART是一种无教师、矢量聚类、竞争学习算法。它成功地解决了学习中的稳定性(固定某一分类集)与可塑性(调整网络固有参数的学习状态)之间的矛盾。

3.2 ART神经网络学习方法

传统ART神经网络算法的学习方法详见参考文献[6]。

由于在实际情况中,各传感器性能不尽相同以及外部条件等因素的影响,不一定会有多少个传感器就反馈回多少个目标参数,由此造成空间向量分布不均匀的特点。初始设置的警戒参数在聚类过程中往往会存在主观性和全局性等缺陷,使得分类效果不均,降低跟踪精度,故对警戒参数调整规则如下:

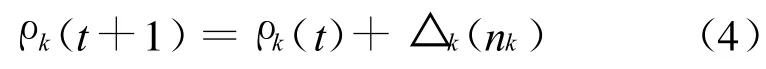
修正量△k(nk)使新的警戒参数和原始警戒参数与空间向量的密度成同向关系。当类别内包含较密集的输入向量时差值较大,形成的新警戒参数值较大,在新一次聚类循环中此类将被细分为较多的子类别;而当类别内输入向量较稀疏时差值较小,形成的新警戒参数值较小,在新一次聚类循环中此类别会被划分为较少的几个子类别。

4 多目标数据关联

M个传感器(局部节点)跟踪T个目标的动力学方程为:

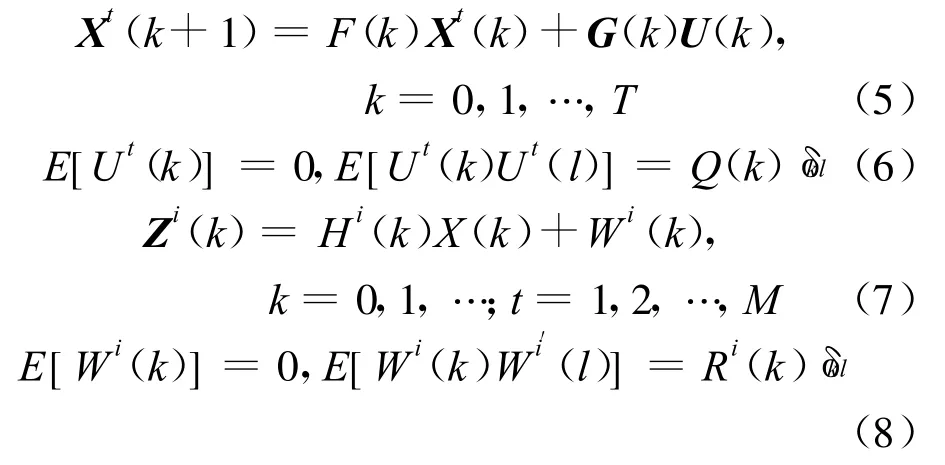
式中:X(k)为k时刻状态向量;过程噪声U(k)和测量噪声Wi(k)均为高斯过程,协方差分别为Q(k)、R(k);Zi(k)为第i个传感器在k时刻的测量矢量。

4.1 数据关联过程

设有N个传感器对M个目标进行跟踪,在杂波环境下,每个传感器得到的量测数据可能来自目标也可能来自杂波,这时就需要用数据关联将传感器的量测区分开来。把目标数作为聚类个数c,传感器得到的观测数据作为样本点,目标状态预测值作为类的中心,设传感器融合系统系统已形成航迹,且各传感器的量测数据在时间上同步,在空间上已转换为同一坐标系,则数据关联的具体步骤如下:

(1)由k时刻目标t的状态融合估计,在Kalman状态估计滤波后到k+1时刻各个目标的状态预测 xj′(k+1/k)、新息vjt(k+1)及信息协方差阵Sjt(k+1)。目标状态预测即为k+1时刻传感器融合系统得到的量测分类中心作为ART神经网络“粗聚类”的初始聚类中心。

(2)根据ART神经网络学习方法对输入数据Xi(i=1,2,…,n)按照以Kalman状态估计滤波得到的初始聚类中心进行“粗聚类”。对于匹配度较差的量测点,很明显是杂波,因此利用ART神经网络先行排除。网络收敛后,根据输出节点的响应,完成样本数据集的聚类。

(3)输出聚类数目C和聚类中心Z={Z1,Z2,…,ZC}。

(4)进行模糊C均值聚类,计算各测量点对聚类中心的隶属度矩阵U。对加权指数m的取值,文献[3]根据聚类有效性问题结果,采用取值范围1.5≤m＜2.5,选择加权指数m=2。这是一个最简洁的取值,较具有代表性。

由于任一目标只能有一个观测量来自同一个传感器,因此把多传感器观测数据聚类转化为多个单传感器聚类,把源于同一个传感器的观测量按最大隶属度来分配给各个目标,这样有效降低了聚类的复杂度,避免了错误关联的概率,更符合实际。

因此本文基于ART神经网络的FCM聚类算法大致可分为2个阶段:第1阶段,由ART神经网络进行初聚类——“粗聚类”,在排除显著的杂波干扰前提下得出聚类数目和各类中心点;第2阶段,将第一阶段的聚类输出结果作为FCM聚类的初始输入,进行迭代比较,直至收敛并输出聚类信息。

4.2 数据融合与跟踪滤波

4.2.1 传感器观测数据融合

由于每个传感器测量误差不尽相同,故σw2(i)可能两两不等,其中i=1,2,…,N。对经过数据关联的某N个量测组成的一类C={Zi(tc)│i=1,2,…,N}作线性组合。

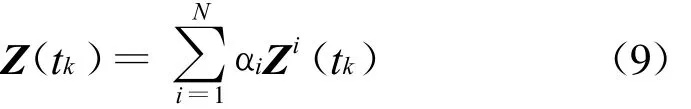
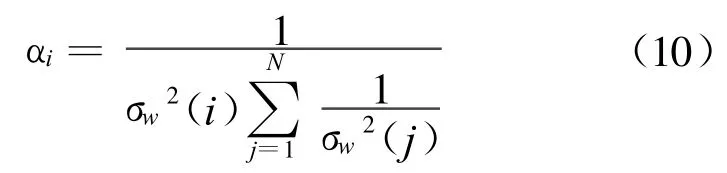
4.2.2 跟踪滤波

完成量测与目标的互联后,下一步便是更新目标的状态,预测目标的新状态了。对于新目标,则是产生目标的轨迹,同时预测其下一时刻的状态。对于已测得的轨迹,利用Kalman滤波器得出当前时刻的状态及下一时刻的估计状态,计算步骤如下:

(1)验前状态估计(预测)方程:

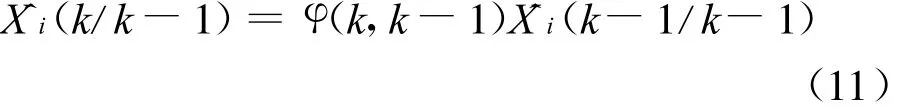
(2)验后状态估计(滤波)方程:

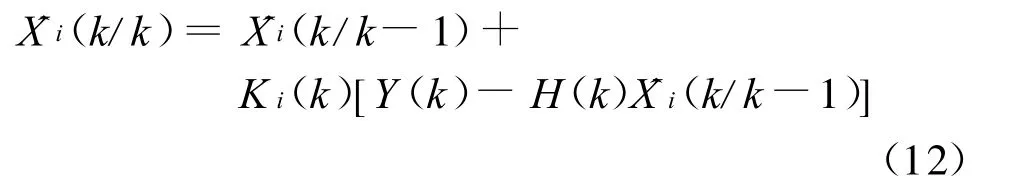
(3)卡尔曼滤波增益(最优增益)方程:

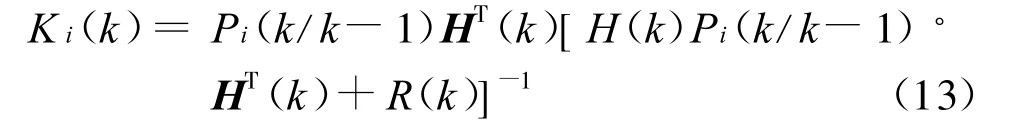
(4)验前误差协方差(预测)方程:

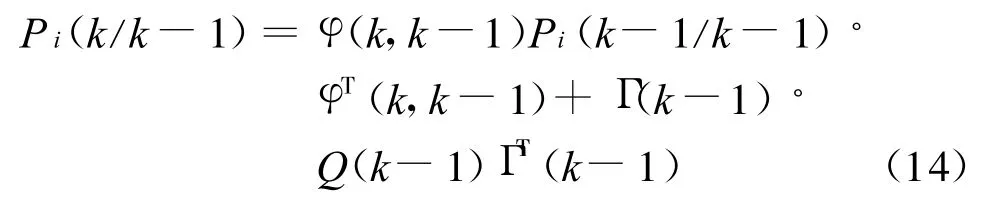
(5)验后误差协方差(滤波)方程:

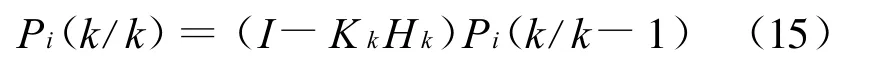
5 仿真实验

仿真战场范围是一个11 km×11 km的空间区域,仿真时间为40 s,其中杂波密度为1×10-5个/km3。假设只有位置测量可以利用,忽略目标在高度范围内的变化。战场中舰艇编队共有2艘驱逐舰,采用大间距单纵队防御队形,每艘舰艇有两部传感器提供量测数据,融合中心设在第一艘舰艇上。仿真程序每隔1 s发送一批仿真数据,这些数据是传感器在场景中采集到的信息,包括位置和速度,并进行100次Monte Carlo仿真实验。

航路想定:本仿真采用4部传感器实时提供的量测数据,传感器的测量精度(均方误差)为100 m,跟踪2个做近似交叉机动的目标。

目标1:初始位置位于5000m,初始速度为200 m/s,初始加速度为-10 m/s2,目标以大约2°/s的角速度进行转弯运动;

目标2:初始位置位于8 600 m,初始速度-200 m/s,初始加速度10 m/s,目标以大约2°/s的角速度进行转弯运动;

其中,目标1与目标2在第10～25个采样周期进行近似交叉机动,仿真及跟踪轨迹如图1(a)、(b)所示,。

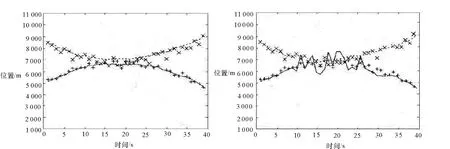
图1 跟踪效果比较

由表1、2可明显看出,在中等杂波条件下,初始机动跟踪时,两算法跟踪精度及数据关联正确率相差不大;但到两目标进行交汇机动时(10～25 s左右),传统算法跟踪效能明显不如改进后算法跟踪效能,容易出现目标的合并或丢失,而错误估计甚至无法估计目标,增加了误警概率,导致跟踪精度明显降低,见表1、2。从反应时间上,传统算法为 4.5 s,本文提出的模型算法比其提高了近50%,为2.4 s,为武器系统的有效利用,提高编队整体防御预警时间,提供了有力的基础。

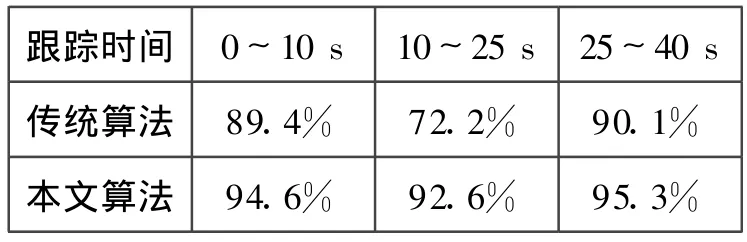
表1 两种跟踪算法平均关联正确率对比

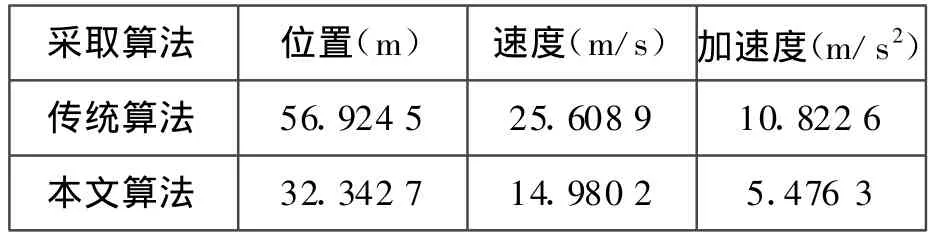
表2 两种跟踪算法跟踪精度对比(x轴均方误差平均值)

6 结论

本文利用ART算法自动聚类的优点对数据集先行“粗聚类”,克服了FCM算法的性能强烈依赖类中心的初始化,初始类中心又是随机选取的不足。通过将改进的ART神经网络与FCM算法的结合,达到了减少算法的迭代次数,缩减聚类时间,并很快收敛于实际的类中心的效果。仿真实验表明,对观测值进行ART-FCM聚类处理后的滤波跟踪航迹精度较高,时间较短,对多目标跟踪理论的实际应用有一定的理论参考价值。

[1]胡炜薇,李争,蒲书绍,杨苹元.杂波环境下雷达组网的多目标聚类融合跟踪[J].哈尔滨工程大学学报,2006,27(4):584-587.

[2]Bezdek C James.Convergence theoryfor fuzzy cmeans:counter examples and repairs[J].IEEE Transaction on Systems,Man and Cybernetics,1987,17(6):889-914.

[3]陈松生.王蔚.改进的快速模糊C-均值聚类算法[J].计算机工程与应用,2007,43(10):167-169.

[4]由大德,程树昌,嵇成新,等.火控理论基础[M].大连:海军大连舰艇学院,2005.

[5]钱晓东.基于改进ART2算法的数据聚类方法[J].计算机工程与设计,2007,28(11):2629-2632.

[6]王永骥.涂健.神经元网络控制[M].北京:机械工业出版社,1999.

[7]徐毓,李锋,金以慧.基于聚类融合的多目标跟踪算法[J].传感器技术,2002,21(7):31-34.