基于储量价值评估的油田开发规划模型及应用①
迟国泰,王化增,程砚秋
(大连理工大学 管理学院,辽宁 大连 116024)
一、引 言
油田开发规划是指通过分析油田开发的状况、限制条件,协调油田各个开发规划目标之间的关系,确定油田开发的目标,提出实现目标的最佳执行方案,使油田开发既遵循自身规律,又能实现高效的可持续发展。现有油田开发规划研究大体可以分为4类:一是以总成本最低为目标函数的油田开发规划研究。代表性人物主要有Babayev[1]、张在旭[2]和刘志斌等[3]。二是以产量最大为目标函数的油田开发规划研究。代表性人物主要有刘志斌[4]和辛文等[5]。三是以利润最大为目标函数的油田开发规划研究。代表性人物主要有 McFarland[6]、Wackowski[7]、殷爱贞[8]、宋艳波[9]和张圆圆[10]等。四是油田开发的多目标规划研究。代表性人物主要有范江[11]、尚明忠[12]和刘志斌[13]等。
现有油田开发规划研究仍存在的主要问题:一是现有油田开发规划[13]采用规划年的原油价格作为整个开发规划期的原油价格,忽略了原油价格具有很强波动性的特点。二是现有油田开发规划[2]对新投产油井的产量、已往投产油井的产量未加区分地等同看待。三是现有油田开发规划或是研究油田开发某阶段最佳井数的确定[11]或是研究整个油田开发过程开发总井数的确定[2],较少关注整个油田开发过程中各阶段最佳井数确定的问题。
针对现有研究存在的上述三个问题,本文分别提出如下解决思路:
思路1:本文综合考虑整个开发规划期内欧佩克的目标价格区间 (438美元/吨—584美元/吨[14])和近三年国际油价的实际水平 (438美元/吨—730美元/吨[14]),通过随机函数确定开发规划期内各年的原油价格。
思路2:本文根据油田的初始产量Q0、加权平均自然递减率d分别测算在规划期内未来第k年新投产油井的产量和未来第1年至第k-1年投产油井的产量,其中,第k-1年投产油井的产量等于(1-加权平均自然递减率d)倍的第k年投产油井的产量,真实地反映了油井产量逐年递减的客观规律,克服了现有研究将新投产油井、已往投产油井的产量等同看待的问题。
思路3:本文对油田开发中累计净现值最大的总目标函数进行分阶段求解,确定了油田开发各阶段的最佳井数,改变了现有研究较少关注整个油田开发过程中各阶段最佳井数确定的问题。一是以油田开发规划过程中各阶段最佳井数xk为决策变量,建立了油田储量从第1年至第n年的累计净现值最大化的目标函数。二是将石油储量开发规划的总目标函数转化为多个各阶段目标函数。三是通过对各阶段目标函数进行优化,确定了油田开发各阶段的最佳井数。其原理如图1所示。

图1 基于储量价值评估的油田开发规划原理
二、基于储量价值评估的油田开发规划模型的建立
(一)参数的确定
1.原油价格的确定
原油价格受到国际政治、经济、汇率以及投机炒作等多方面因素影响,具有波动性强、预测准确度低的特点。现有储量价值评估方法多采用评估期初的价格作为原油价格。而规划初期的原油价格与实际价格水平往往存在较大差异。本文综合考虑规划期内欧佩克的目标价格区间 (438美元/吨—584美元/吨)和近三年国际油价的实际水平 (438美元/吨—730美元/吨),通过随机函数rand确定原油价格。
设:[a,b]为原油价格的波动区间,[a1,b1]为规划期内欧佩克的目标价格区间,[a2,b2]为近三年国际原油价格区间,则确定规划期原油价格波动区间为:

其中,规划期原油价格波动区间 [a,b]的左端点a取欧佩克的目标价格区间 [a1,b1]的左端点a1和近三年国际原油价格区间 [a2,b2]的左端点a2的最小值。规划期原油价格波动区间 [a,b]的右端点b取欧佩克的目标价格区间 [a1,b1]的右端点b1和近三年国际原油价格区间 [a2,b2]的右端点b2的最大值。
设:pk为第k年的原油价格,rand(a,b)为随机函数,随机生成一个属于区间 [a,b]的数值,服从 [a,b]上的均匀分布,则能确定原油价格序列:

式 (2)通过随机函数确定第k年的原油价格pk。由式 (3)知,第k年的原油价格pk服从 [a,b]上的均匀分布,其原因是:第k年的原油价格pk是区间 [a,b]内的任何一点,其概率密度详见参考文献 [15]。这一过程可以方便地通过随机函数rand实现[15]。
2.油田产量水平
油田产量水平主要取决于孔隙度、含油饱和度等地质条件,还与油藏类型和开发工艺密切相关。本文采用类比法[16]确定油田产量的初产水平Q0。
3.油田产量的自然递减率
油田开发一定时间后,产量将按照一定的规律递减。油田产量的自然递减率是指扣除各种增产措施增加的产量之后,下一阶段采油量与前一阶段采油量之比。
设:d为加权平均自然递减率,di为第i年自然递减率,wi为第i年自然递减率权重系数,n为项目总的开采年限 (本研究中n=20年),则:

式 (4)的含义是油田产量第i年自然递减率di和权重系数wi的乘积。
式 (5)的含义是油田产量第i年自然递减率di作用年限 (n-i+1)占油田产量全部自然递减率di作用年限的比重。这样做的好处是:油田产量第i年自然递减率di作用年限 (n-i+1)越长,油田产量第i年自然递减率di的权重系数wi越大。
计算加权平均自然递减率d,通过油田产量加权平均自然递减率d分别对第k年新投产油井的产量和累计至第k-1年末拥有的油井产量进行加权,真实地反映了油井产量逐年递减的客观规律,克服了现有研究将新投产油井、已往投产油井的产量等同看待的问题。
应该指出,本文采用类比法确定式 (4)中的油田产量第i年的自然递减率di,即将渗透率、绝对渗透率、地层压力等地质条件相似的油田区块的第i年的自然递减率di作为研究乌兹别克斯坦安基延油田第i年的自然递减率di。
4.总井数的确定
设:sk为第k年末的总井数,xk为第k年新投产井数,SN为储量开采项目的设计总井数,SL为年度钻井工程可用资金总额所决定的钻井数,n为项目总的开采年限,则:

式 (7)的含义是:第k年新投产井数xk大于等于0,小于等于第k年末的总井数sk和储量开采项目的设计总井数SN中的最小值。
应该指出,年度钻井工程可用资金总额所决定的钻井数SL可以通过式 (8)确定。
设:SL为年度钻井工程可用资金总额所决定的钻井数,M为每年钻井资金限制,C1'为单井钻井费用,C2'为单井投产及地面建设费用,则:

式 (8)的含义是:每年钻井资金M除以单井开发费用 (C1'+C2')就是年度钻井工程可用资金总额所决定的钻井数SL。其中,单井开发费用 (C1'+C2')包括单井钻井费用C1'和单井投产及地面建设费用C2'。
5.第k年的现金流
第k年的现金流vk包括第k年新投产井产生的净现金流vk1和累计至第k-1年末拥有的油井产生的净现金流vk2。
(1)第k年新投产井产生的净现金流vk1
设:vk1为第k年新投产井产生的净现金流,xk为第k年新投产井数,Q0为单井年产量,d为加权平均自然递减率,pk为第k年的原油价格,t为税金及其附加,C1为钻井费用,C2为投产及地面建设费用,C3为操作成本,则[17]:

式 (9)的含义是第k年新投产井产生的净现金流。其中,第k年新投产井产生的现金流入为第k年新投产井的销售收入 (xk×Q0× (1-d)×pk),第k年新投产井产生的现金流出包括税金及其附加t、第k年新投产井的投资额C1+C2+C3。
(2)累计至第k-1年末拥有的油井产生的净现金流vk2
设:vk2为累计至第k-1年末拥有的油井产生的净现金流,xi为第i年新投产井数,Q0为单井年产量,d为平均自然递减率,pk为第k年的原油价格,t为税金及其附加,C3为操作成本,则[17]:

式 (10)的含义是累计至第k-1年末拥有的油井产生的净现金流。
应该指出,式 (9)与式 (10)是油田开发规划第k年现金流的两部分。其中,式 (9)表示第k年新投产井产生的净现金流vk1,式 (10)表示累计至第k-1年末拥有的油井产生的净现金流vk2。
(3)第k年的净现金流vk
设:vk为第k年的现金流,vk1为第k年新投产井产生的净现金流,vk2为累计至第k-1年末拥有的油井产生的净现金流,则:

6.第k年的净现值
设:NPVk为第k年的净现值,vk为第k年的现金流,r为财务贴现率,则[17]:

(二)基于储量价值评估的油田开发规划模型
1.目标函数
(1)目标函数的建立
设:NPV为从第1年至第k年末累计的净现值,n为项目总的开采年限,NPVk为第k年的净现值。通过使从第1年至第n年末累计的净现值NPV最大建立模型目标函数为:
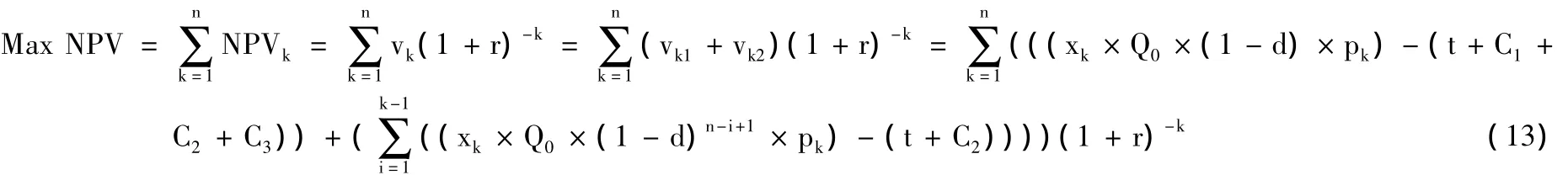
式 (13)的含义是第1年至第n年的净现值总和最大化。这样做的好处是保证油田储量从第1年至第n年的累计净现值最大。
(2)各阶段目标函数的建立
由式 (13)可知,油田储量从第1年至第n年的累计净现值最大化以第i年新投产井数xi(1≤i≤n)为变量。下面分别建立油田开发的最后一年、油田开发规划的第j年和油田开发规划的第1年的目标函数。
第一,油田开发规划最后一年的目标函数
在油田开发的最后一年 (第n年),式 (13)可以用式 (14)表示。
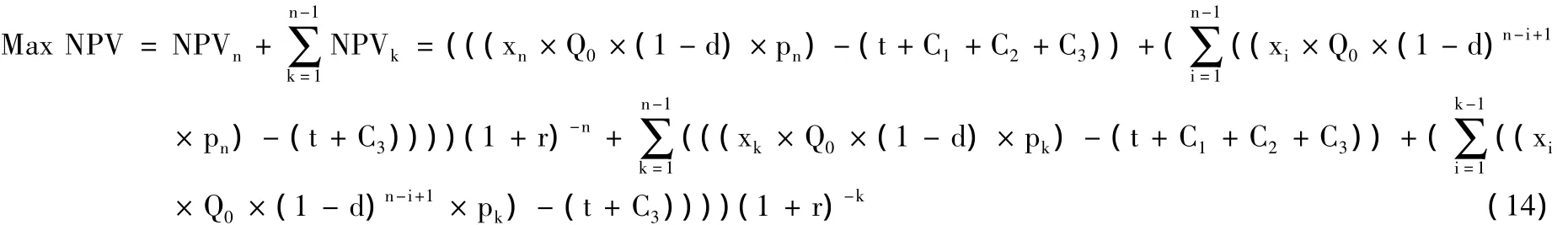
油田开发的最后一年 (第n年),式 (14)的含义是油田储量从第1年至第n年的净现值总和最大化,也就是油田第n年的净现值、油田前n-1年的净现值的总和最大化。
由式 (14)可知,在油田开发的最后一年 (第 n年),油田前 n-1年的净现值是定值,故式 (14)最大化仅与油田第n年的净现值NPVn有关。
第二,油田开发的第j年 (1<j<n)的目标函数
在油田开发的第j年 (1<j<n),式 (13)可以用式 (15)表示。
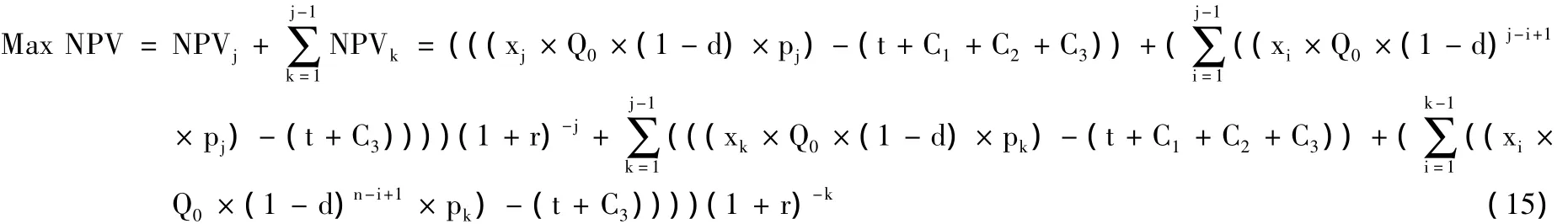
油田开发的第j年,式 (15)的含义是油田储量第1年至第j年的净现值总和最大化。
由式 (15)可知,油田开发的第j年 (1<j<n),油田前j-1年的净现值是定值故式 (15)最大化仅与油田第j年的净现值NPVj有关。
第三,油田开发规划第1年的目标函数
油田开发的第1年,式 (13)可以用式 (16)表示。
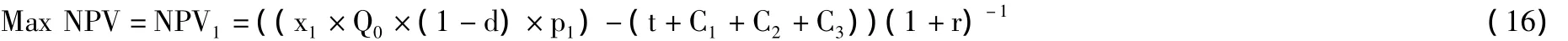
油田开发的第1年,式 (16)的含义是油田第1年的净现值NPV1最大化。
综上,式 (13)—(16)建立了油田各开发规划阶段的累计净现值最大化的目标函数。
2.约束条件的建立
由式 (6)—(7)得到约束条件。
(1)累计油井数sk的约束条件
设:sk为从第1年至第k年末累计油井数,xk为第k年新投产井数,SN为储量开采项目的设计总井数,则累计油井数sk的约束条件为:

(2)第k年新投产井数xk的约束条件
设:sk为从第1年至第k年末累计油井数,xk为第k年新投产井数,SL为第k年资金容许下可能形成的井数,则第k年新投产井数xk的约束条件为:

3.开发规划模型的建立
以式 (13)—(16)为目标函数,以式 (17)—(18)为约束条件,建立了基于储量价值评估的油田开发规划模型,保证了油田储量从第1年至第n年的累计净现值最大。
其中,式 (13)为油田开发规划的总目标函数。式 (14)—(16)为油田开发规划的分阶段目标函数,式 (14)为油田开发规划最后一年的目标函数,式 (15)为油田开发规划第j年的目标函数,式 (16)为油田开发规划第1年的目标函数。
三、应用实例与对比分析
(一)基本数据及处理
1.油田基本数据
本文采用乌兹别克斯坦安基延油田的数据[18-19]。实证研究乌兹别克斯坦安基延油田的单井日产量为17吨/天,每年生产天数为300天。总开发年限n为20年,开发规划方案中总井数SN为110口。此油田每年钻井资金限制M为2 000万美元,平均井深为1 500米,钻井成本为500美元/米,单井投产费用为161千美元,单井地面建设费为249千美元。此油田综合税金及附加费t为销售收入的17%,现金操作成本为39.055美元/吨,单井初始年产量为300吨,贴现率取14%。
2.相关参数的计算
(1)单井年产量Q0
根据油田基本数据中的单井日产量、油井每年生产天数计算单井年产量Q0。

(2)油田产量的平均自然递减率d
本文通过类比法得到乌兹别克斯坦安基延油田的自然递减率,如表1第3行第3—22列所示。将表1第3行第3—22列数据代入式 (4)得加权平均自然递减率d=15%。
(3)原油价格pk
将评估期内欧佩克价格区间 (438美元/吨—584美元/吨)和近三年国际油价的实际水平 (438美元/吨—730美元/吨)代入式 (1),得到规划期间原油价格的波动区间为 [438美元/吨,730美元/吨]。根据乌兹别克斯坦安基延油田的总开发年限n=20年,从规划期间原油价格的波动区间[438美元/吨,730美元/吨]随机选取20个数,作为原油价格序列pk,列入表1第4行第3—22列。这一过程可以方便地通过随机函数rand实现[15]。
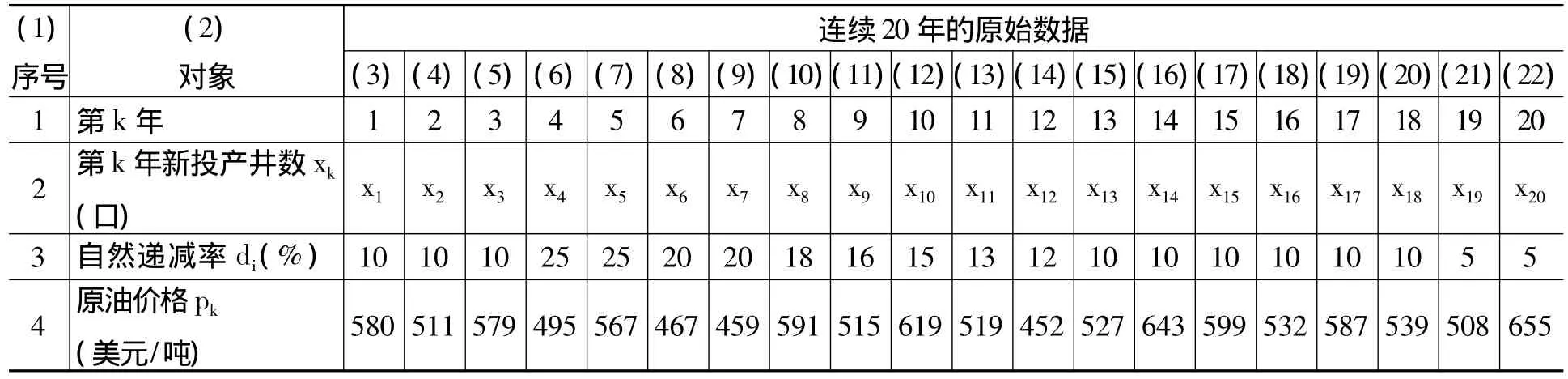
表1 连续20年的原油价格和自然递减率
(4)单井钻井费用C1'
根据油田基本数据中的平均井深、每米的钻井成本计算单井钻井费用C1'。
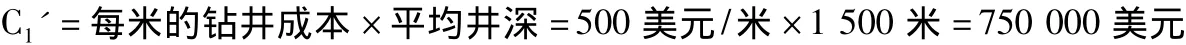
(5)单井投产及地面建设费用C2'
根据油田基本数据中的单井投产费用、单井地面建设费计算单井投产及地面建设费用C2'。
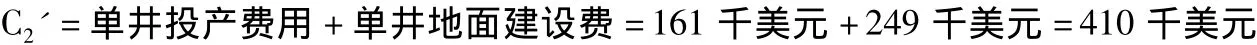
(6)第k年资金容许下可能形成的井数SL
根据油田基本数据中的每年钻井资金限制M、单井钻井费用C1'、单井投产及地面建设费用C2'计算第k年资金容许下可能形成的井数SL。
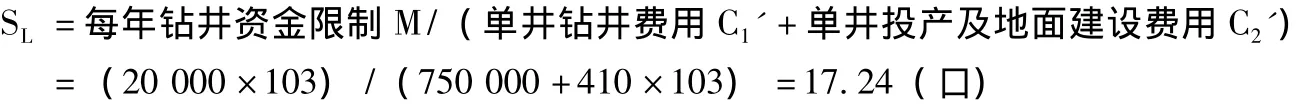
(二)油田第1年的开发规划
1.第1年油田开发目标函数的建立
在本文中,第1年就是油田开发的第1期,应该运用式 (16)求解油田开发规划的目标函数。
将前文的的油田基本数据、相关参数和表1第1—4行第3列的数据代入式 (16),则第1年的目标函数为:
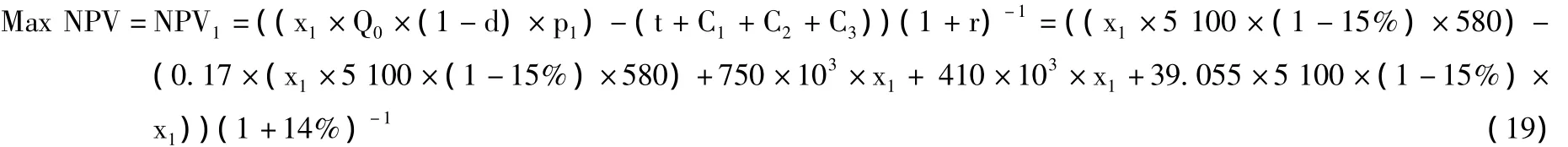
2.第1年油田开发约束条件的建立
(1)第1年累计油井数s1的约束条件
将前文的开发规划方案中预计钻110口井,代入式 (17),得累计油井数s1的约束条件为:

即累计油井数s1的取值范围是从0到110的所有整数。
(2)第1年新投产油井数x1的约束条件
将前文的开发规划方案中预计钻110口井、累计油井数s1的年度钻井工程可用资金总额所决定的钻井数sL=17.24代入式 (18),则第1年新投产井数x1的约束条件为:

3.第1年油田开发规划
求解由目标函数式 (19)及约束条件式 (20)、(21)组成的线性规划模型[13],可得出油田开发的第1年最优方案,列入表2第1行第3列。上述过程可以利用Visual C++编程求解。
将表2第1行第3列的优化结果代入目标函数式 (19)得到第1年的累计净现值10 609.16千美元,如表2第1行第4列所示。

表2 开发方案及评估结果
(三)油田第2年的开发规划
1.第2年油田开发目标函数的建立
在本文中,第2年就是油田开发的第2期,应该运用式 (15)求解油田开发规划的目标函数。
将前文的油田基本数据、相关参数和表1第1—4行第4列的数据以及表2第1行第4列的数据代入式 (15),则第2年的目标函数为:
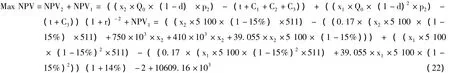
2.第2年油田开发约束条件的建立
(1)第2年累计油井数s2的约束条件
将前文的开发规划方案中预计钻110口井,代入式 (17),得累计油井数s2的约束条件为:

(2)第2年新投产油井数x2的约束条件
将前文的开发规划方案中预计钻110口井、累计油井数s2和年度钻井工程可用资金总额所决定的钻井数sL=17.24代入式 (18),则第2年新投产井数x2的约束条件为:

3.第2年油田开发规划
求解由目标函数式 (22)及约束条件式 (23)、(24)组成的线性规划模型[13],可得出油田开发的第2年最优方案,列入表2第2行第3列。上述过程可以利用Visual C++编程求解。
将表2第2行第3列的优化结果代入式 (22)得第2年累计净现值,列入表2第2行第4列。
仿照油田第1、第2年开发规则,运用表1第4—22列的数据、表2第1—2行第3—4列的优化结果,可得出油田开发第3—20年的最优方案和累计净现值。
(四)对比分析
1.对比分析所采用的模型及其结果
(1)对比分析所采用的模型
本文所采用的5个对比分析模型如表3所示。

表3 对比分析所用模型
模型1:本文所建立的基于储量价值评估的油田开发规划模型。它通过式 (13)保证油田储量从第1年至第k年末累计的净现值最大。
模型2:基于评估初期原油价格的油田开发规划模型。在模型1的基础上,第k年的油价pk用评估期初的油价p1替代。
以油田第1年的开发规划为例,其目标函数如 (19)式所示,约束条件如 (20)、(21)式所示。
模型3:基于算术平均自然递减速率的油田开发规划模型。在模型1的基础上,加权平均自然递减率d用式 (25)的算术平均自然递减率d'替代。

以油田第1年的开发规划为例,其目标函数为:
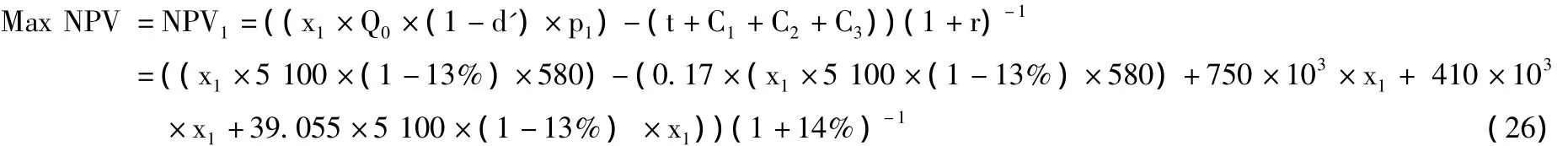
约束条件为:

模型4:基于原开发方案的油田开发规划模型。在模型1的基础上,油田钻井开发方案用油田原有的开发方案替代,即第k年新投产井数xk不是采用最优方案得到,而是采用现有方案中的规划xk'。现有油田开发规划方案xk'如表2第9列所示。
油田开发规划第1年的净现值为:
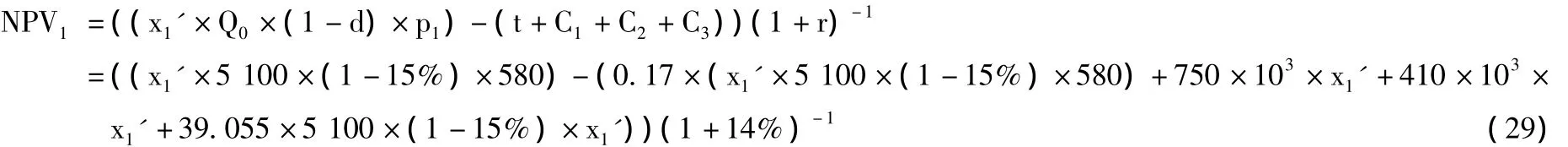
模型5:基于评估初期原油价格—算术平均自然递减速率—原开发方案的油田开发规划模型。在模型1的基础上,第k年的油价pk用评估期初的油价替代,油田的加权平均自然递减率d用算术平均自然递减率替代,油田钻井开发方案xk用油田原有的开发方案xk'替代。现有油田开发规划方案xk'如表2第11列所示。
油田开发规划第1年的净现值为:
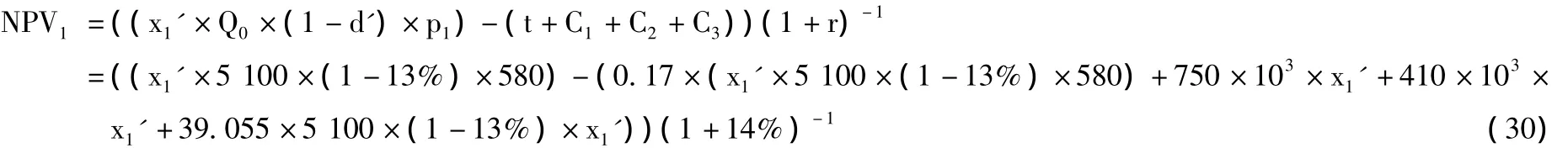
(2)对比分析模型的结果第一,模型2的优化结果
求解目标函数为式 (19)、约束条件为式 (20)—(21)的线性规划模型2[13],可得油田开发规划的优化结果如表2第5列第1行所示。将表2第5列第1行的分配结果代入式 (19)得到累计净现值,如表2第6列第1行所示。
同理,运用表1第4—22列的数据和表2第1行第5列的优化结果,可得出模型2油田开发第2—20年的方案和累计净现值。模型2油田开发第2—20年的方案如表2第2—20行第5列所示。累计净现值如表2第2—20行第6列所示。
第二,模型3的优化结果
求解目标函数为式 (26)、约束条件为式 (27)—(28)的线性规划模型3[13],可得油田开发规划的优化结果,列入表2第7列第1行。将表2第7列第1行的分配结果代入式 (26)得到累计净现值,如表2第8列第1行所示。
同理,运用表1第4—22列的数据和表2第1行第7列的优化结果,可得出模型3油田开发第2—20年的方案和累计净现值。模型3油田开发第2—20年的方案如表2第2—20行第7列所示。累计净现值如表2第2—20行第8列所示。
第三,模型4的优化结果
现有油田开发规划方案如表2第9列所示。将表2第1行第9列的数据代入式 (29)得模型4第1年的净现值,如表2第1行第10列所示。
同理,运用表2第1—20行第9列的数据可得模型4第2—20年的净现值,如表2第2—20行第10列所示。
第四,模型5的优化结果
现有油田开发规划方案如表2第11列所示。将表2第1行第11列的数据代入式 (30)得模型5第1年的净现值,如表2第1行第12列所示。
同理,运用表2第1—20行第11列的数据可得模型5第2—20年的净现值,如表2第2—20行第12列所示。
2.对比分析的结论
模型1和模型2的最优开发规划方案一样。由表2第3列和第5列知,模型1的最优开发方案和模型2的最优开发方案是一样的。模型2的累计净现值高于模型1的累计净现值。由表2第20行第4列和第6列知,模型2的累计净现值高于模型1的累计净现值。由表1第6行第3—22列知,规划初期原油价格较高导致了模型2的累计净现值较高。
模型1和模型3的最优开发规划方案一样。由表2第3列和第7列知,模型1的最优开发方案和模型3的最优开发方案是一样的。模型3的累计净现值高于模型1的累计净现值。由表2第20行第4列和第8列知,模型3的累计净现值高于模型1的累计净现值。由表1第4行第3—22列知,加权平均自然递减率较高导致了模型1的累计净现值较低。
模型1的累计净现值高于模型4的累计净现值。由表2第20行第4列和第10列知,模型1的累计净现值高于模型4的累计净现值。
模型1的累计净现值高于模型5的累计净现值。由表2第20行第4列和第12列知,模型1的累计净现值高于模型5的累计净现值。
四、结 论
本文以油田累计净现值最大化为目标函数,以油田开发资金限制为约束条件,建立了油田储量开发规划模型,并采用乌兹别克斯坦安基延油田的数据进行实证研究。
第一,通过对油田开发规划总目标函数的分阶段求解,确定了油田开发各阶段的最佳井数,改变了现有研究较少关注整个油田开发过程中各阶段最佳井数确定的问题。一是以油田开发规划过程中各阶段最佳井数xk为决策变量,建立了油田储量从第1年至第n年的累计净现值最大化的目标函数。二是将油田储量开发规划的总目标函数转化为多个各阶段目标函数。三是通过对各阶段目标函数进行优化,确定了油田开发各阶段的最佳井数。
第二,综合考虑规划期内欧佩克的目标价格区间和近三年国际油价的实际水平,通过随机函数确定原油价格,反映了原油价格变动的特点;避免了现有研究采用规划初期的原油价格作为整个规划期的原油价格的问题。
第三,根据油田的初始产量Q0、加权平均自然递减率d分别测算在规划期内未来第k年新投产油井的产量和未来第1年至k-1年投产油井的产量,真实地反映了油井产量逐年递减的客观规律,克服了现有研究将新投产油井、已往投产油井的产量等同看待的问题。
[1]Babayev D.A.Mathematical Models for Optimal Timing of Drilling Multilayer Oil and Gas Fields[J].Management Science,1975,21(12):1361 -1369.
[2]张在旭,冯德田.油田开发规划模型[J].系统工程理论与实践,1997,5(5):124-127.
[3]刘志斌,丁辉,高珉,等.油田开发规划产量构成优化模型及其应用[J].石油学报,2004,25(1):62-65.
[4]刘志斌,贾闽慧,康小军.石油生产函数及在产量最大化中的应用[J].西南石油学院学报,2006,28(6):98-99.
[5]辛文,詹婷婷.石油企业优化决策与油田开发规划[J].知识经济,2009,24(9):111-112.
[6]McFarland J.W.,Lasdon W.L.,Verne L.Development Planning and Management of Petroleum Reservoirs Using Tank Model and Non - Linear Programming[J].Operations Research,1984,32(2):270 -289.
[7]Wackowski R.K.,Stevens C.E.,Masoner L.O.,Attanucci Vince,Larson J.L.,Aslesen K.S.Applying Rigorous Decision Analysis Methodology to Optimization of a Ter- Tiary Recovery Project:Rangely Weber Sand Unit,Colorado [M].London:Society of Petroleum Engineers,1992.24-34.
[8]殷爱贞,张在旭,李嘉庆.油田产量优化的目标规划模型[J].石油大学学报(自然科学版),2003,27(5):119-121.
[9]宋艳波,潘志坚,胡永乐,等.适用于油气田配产的交互式规划新方法[J].天然气工业,2004,24(12):149-151.
[10]张圆圆,叶鹏.油田开发多年规划单目标产量优化模型及应用[J].断块油气田,2009,16(6):59-61.
[11]范江.确定油田开发最佳井数的多目标数学规划方法[J].石油学报,1996,17(4):105-108.
[12]尚明忠,盖英杰,李树荣,等.油田开发规划非线性多目标优化模型研究[J].石油钻采技术,2003,31(4):59-61.
[13]刘志斌,张锦良.油田开发规划多目标产量分配优化模型及其应用[J].运筹与管理,2004,13(1):118-121.
[14]British Petroleum.BP Statistical Review of World Energy[EB/OL].http://www.bp.com,2009 -04 -20.
[15]戴维M.莱文,戴维F.斯蒂芬.商务统计轻松学[M].北京:机械工业出版社,2008.93-95.
[16]李斌,张欣赏,刘丹江.类比法定量模型及在油田开发中的应用[J].承德石油高等专科学校学报,2006,8(3):24-27.
[17]李志学.以产量递减和成本递增为基础的石油储量价值评估模型[J].油气地质与采收率,2005,12(l):46-48.
[18]李晓清,王兴科.安基延油区勘探开发潜力分析[R].东营:胜利油田东胜精攻石油开发集团股份有限公司,2007.115-154.
[19]李晓清,孙怀福,马季托夫.乌兹别克斯坦安基延油田开发项目可行性研究报告[R].东营:胜利油田东胜公司与乌兹别克斯坦国家石油公司外资局,2007.53-68.

