H.264/AVC率失真优化技术综述*

马宏兴，张 伶

（北方民族大学 电气信息工程学院，宁夏 银川 750021）

1 引言

H.264/AVC视频编码标[1]在编码模式、编码参数、熵编码、参考帧、高精度预测、去块滤波以及抗误码等方面采取了一系列切合实际的技术措施，相对于H.263和MPEG-4，视频压缩比提高1倍，节约了50%的码率[2]。然而，H.264/AVC仍以传统的混合编码框架为基础，编码器依据图像内容，采用率失真优化的方法[3]，在帧内和帧间众多的可选模式里选取最佳的编码模式，对每一种编码模式都要计算其失真度和比特率，致使编码过程变得复杂，编码时间增加。但是，正是率失真优化技术的应用，H.264/AVC在运动估计及编码模式的选择过程中，尽可能获得最佳运动信息，得到最佳匹配，从而保证了图像的质量，节省码率，整体编码性得到了显著提高。

2 视频编码的率失真理论

视频压缩是典型的限失真编码，率失真理论同样适应于视频编码。视频编码率失真优化指的是在限比特率为R的条件下，即R值不能超过信道传输率Rc，如何选择最佳编码模式，使得失真D最小，约束条件为R≤Rc[4-5]。要实现该目标，在R和D之间必须选择一个恰当的折中。

在实际解决问题的过程中，可由量化步长、宏块编码模式等组成的编码参数集，对视频序列进行编码，得到一系列相应的编码比特率R和失真D点，从而形成R-D率失真曲线。如果给定一个目标码率Rc，与其对应的最小失真D点必然在这一曲线上。视频编码的率失真优化目标正是寻找这些合适的编码参数集，使其代表的R-D点尽可能地位于或接近这条曲线，如图1所示。

约束条件下的极值求解常用拉格朗日乘子法，部分拉格朗日方法不能很好解决的可以用动态规划求解[4]。拉格朗日乘子法能够找出一个或数个性能最好的编码参数集，这些参数可被用于视频编码器以获得最佳的编码性能。但如果编码参数组合的数目极大，率失真计算的复杂性常常比编码算法本身还高，要使率失真优化方法更实用，可以对编码参数简化。

图1 视频编码的R-D模型

3 H.264/AVC率失真优化

3.1 理论分析

根据率失真理论，H.264/AVC视频标准中，每帧图像的编码模式选择问题便是可选模式中最佳模式的选择问题，使得在限定码率Rc下，D最小。

设 X＝｛X1， X2，…， XN｝表示当前帧中的所有宏块，M表示视频编码可选的编码模式集，那么当前帧率失真优化编码就可以表示为

因为H.264/AVC是基于宏块的编码结构，当前帧的失真和码率可以由各个宏块的失真或比特数累加，即有

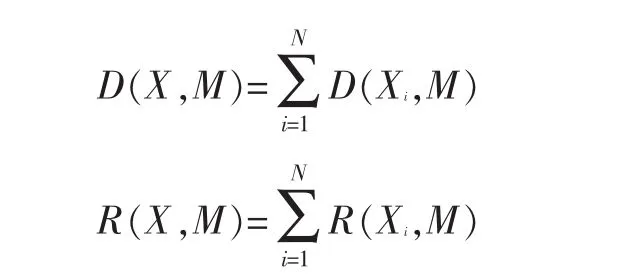
因此，当前帧的率失真函数可以转换成

式中：J（X，M，λ）=D（X，M）+λ×R（X，M）。

显然，只要参数λ可知，该式的极值就可以决定出最优编码模式M*，使得此时的编码失真D（X，M*）就是在限率Rc下的最小失真。但是，由于单个宏块Xi在编码模式M*下的比特数R（Xi，M*）必须在其他所有宏块计算完毕才能获得，所以严格地讲，当前帧各宏块最佳编码模式的决定是相互依赖的，将导致问题非常复杂，难于求解。为了将问题简化，设各宏块的编码模式率失真优化决定是相对独立的，忽略各宏块的码率对其他宏块的编码模式的影响[7]，即有：

式中：Mi表示宏块Xi的编码模式参数集。整帧图像的最优化问题可以进一步分解为

由此，全帧的率失真优化转化为每个宏块的优化，只需要计算单个宏块的率失真开销就行了。

3.2 拉格朗日系数λ的确定

Wiegand等[5-7]依照R-D的近似数量关系和大量的实验结果，得出参数λ与量化步长QP有着某种关系，目前H.264/AVC采用的λ和量化参数QP关系有[3]：

1）对I帧、P帧，如果编码时没有B帧，则

2）对I帧、P帧，如果编码时有B帧，则

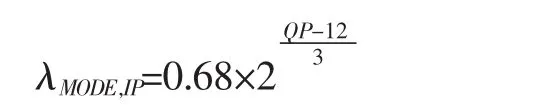
3）对B帧，则有

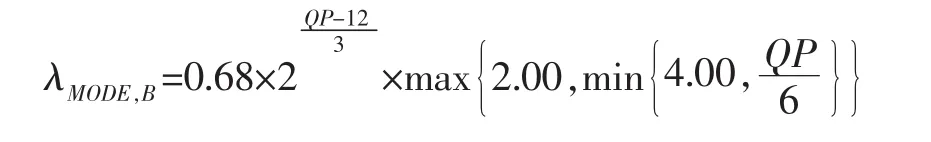
3.3 运动估计的率失真优化

运动估计的率失真优化包括决定最佳运动向量和最佳参考帧及相应的运动信息两个方面。公式分别为

式中：m=（mx，my）T表示运动估计所得到的运动向量；p=（px，py）T表示通过对相邻宏块预测得到的运动向量；λMOTION为拉格朗日参数，R（m-p）表示运动向量差值编码所需比特数，SA（T）D为失真度，计算公式为

式中：B＝16，8 或 4；s表示原始视频信号值；c表示实际编码的视频信号值。如果运动向量是小数精度，则失真度在Hadamard Transform 后采用 SA（T）D 来度量，R（REF）表示选取参考帧REF编码所需的比特数。

3.4 宏块编码模式决定的率失真优化

H.264/AVC在进行宏块模式的选择时，要对各种可选模式进行遍历，计算出每种模式下的编码比特数和失真度，计算公式[8]为

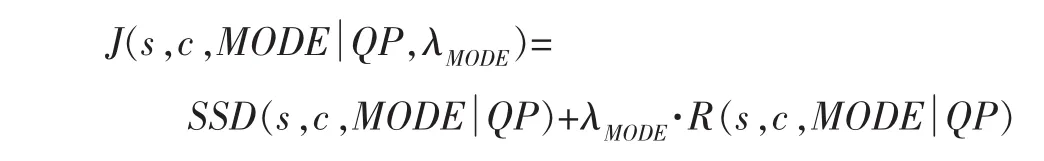
计算拉格朗日函数值J即率失真开销，经过比较，选取最小值下的编码模式MODE做为宏块的最终编码模式。其中QP为宏块的量化参数，s，c分别表示原始图像和重建图像的像素值，R（s，c，MODE|QP）表示在特定QP和 MODE下当前宏块的编码输出比特数，SSD（s，c，MODE|QP）表示图像失真度，计算公式为

式中：λMODE为拉格朗日系数，MODE为当前宏块可选的一种编码模式，针对不同图像类型，编码模式集见表1。

表1 编码模式集

另外，INTRA4×4亦有多种预测模式选择，见图2。

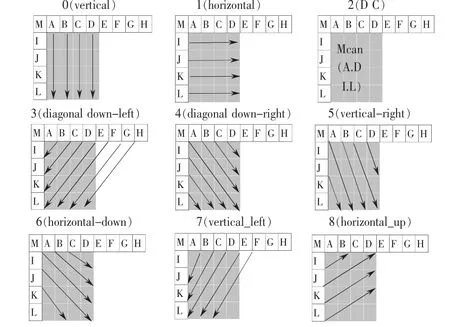
图2 INTRA4×4预测模式

INTRA4×4的预测模式选择率失真优化计算公式为

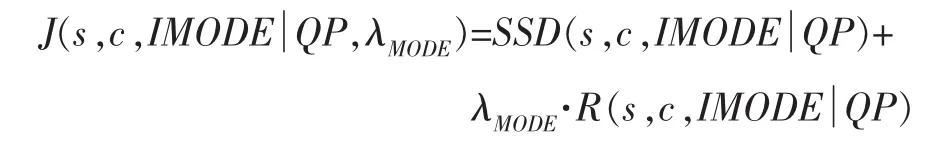
式中 ：IMODE代表可选的多种预测模式，SSD（s，c，IMODE|QP）表示失真，R（s，c，IMODE|QP）表示编码输出比特数，包括帧内预测模式和DCT亮度系数所需比特数。

4 H.264/AVC率失真优化算法及改进情况

4.1 JM7.6率失真优化算法

以测试模型JM7.6为例，下面分析视频标准H.264/AVC在宏块编码所采用的率失真优化算法详细步骤。

算法描述如下：

在三位负责人的带领下，我们身着工作服，参观了从上铝卷到电化学处理、涂布和干燥、在线分切、包装，直至储运、物流的完整生产流程。我们看到，在监控室里高速生产线的实时数据不断闪现，所有数据可以保留2年；生产全过程参数自动检测，全球同步；安装于生产线上的在线检测系统，可检测到50微米缺陷，自动切走缺陷部分；采用环保包装方式，自动打包。此外，我们了解到，其关键材料由总部统一进口；新开发产品，需经过12个月严格测试，才能投入正式生产……或许正因为执行着最严苛的生产要求，无锡工厂才敢于做出最高质量标准的庄重承诺。

1）参数初始化，确定宏块的量化参数QP及参考帧信息，依照当前编码图像类型，计算拉格朗日参数λMODE，λMOTION；

2）决定当前宏块决定最佳INTRA4×4预测模式；

3）通过计算SA（T）D，最小值对应的预测模式为当前宏块最佳INTRA16×16预测模式；

4）为当前宏块选取运动估计的最佳参考帧及相应运动信息；

5）在 2），3），4）基础上，计算各种编码模式下的率失真开销J，选取最小值对应的编码模式作为当前宏块最佳的编码模式；

6）当前宏块编码后续处理，准备下一宏块的编码。

4.2 各种改进率失真优化算法

在H.264/AVC进行编码时，要依据率失真优化，对I，P，B帧的多种模式（见表1）进行遍历计算。但在实际的编码过程中，可以依据图像中的某些相关信息，例如纹理，对编码模式进行预判，从而减少计算的复杂性。D.Wu，F.Pan等人就提出了一种改进的算法[8]，该算法对纹理比较均匀，变化比较缓慢的视频，在视频质量PSNR减少小于0.06 dB时，编码时间可节省近50%。目前，针对H.264/AVC的率失真优化技术的改进较多，大致分为：1）建立视频图像在时间、空间域相关性基础之上的算法，此类方法可处理帧内及帧间众多编码模式；2）建立运动估计和补偿基础之上的率失真算法，利用残差大小在众多编码模式中快速选择。还有诸如基于DCT变换、直方图等改进的率失真优化算法，在此不再一一赘述。

1）如果当前宏块的平均绝对差MAD值小于T1，则当前宏块采用SKIP/DIRECT模式；

2）如果当前宏块的宏块平均绝对差MAD值小于T2，则当前宏块采用 16×16，16×8，8×16 的宏块进行预测；

3）否则，按标准算法进行预测。其中 T1，T2定义如下

式中：MADSKIP/DIRECT为当前宏块之前所采用SKIP/DIRECT模式的宏块所对应的MAD值，MAD16×16为当前宏块之前所采用 16×16 模式的宏块所对应的 MAD 值；△1，△2为修正值，其随着MAD值的变化而变化。

在采用测试模型JM7.6的标准参数时，该算法的实验结果如表2所示，其中△t为所用时间差，△PSNRY为亮度峰值信噪比之差，△Rbit为新算法码率之差，Rbit264为原H.264码率，负值表示改进算法比H.264/AVC算法节省或减少，正值表示增加。由实验结果来看，该算法基本能够保持图像质量，码率没有太大增加的情况下，各种视频序列在编码时间上都有不同程度的节省，从而弥补了标准算法在进行帧间模式选择时计算时间的不足，提高了编码器的工作效率。

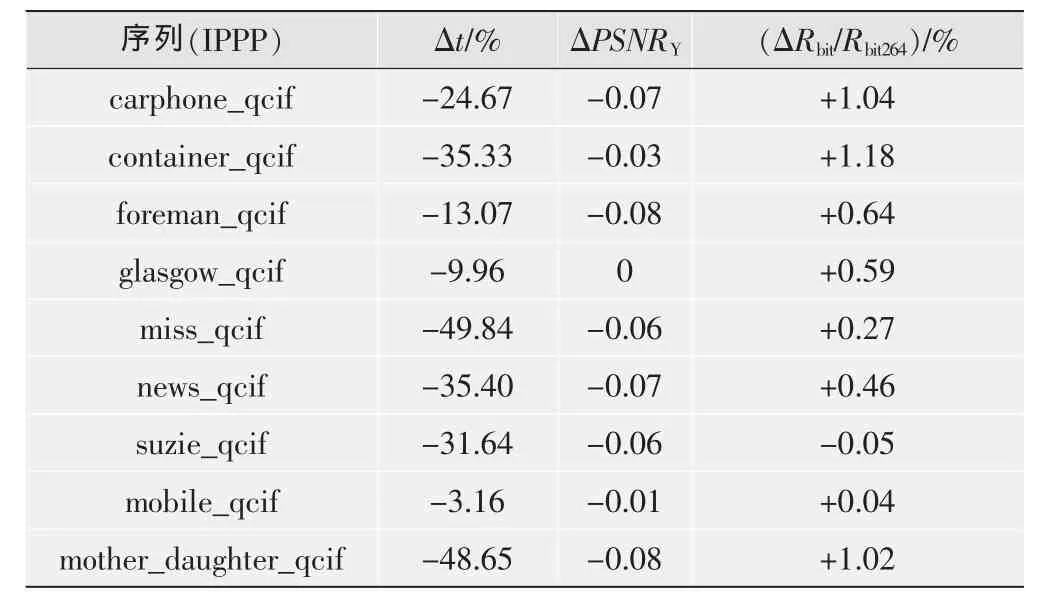
表2 实验结果

5 小结

率失真优化技术是当前图像视频处理中的一项十分活跃的技术，在H.264/AVC视频标准中，其应用虽然保证了图像的质量，节省了码率，但也会致使编码过程变得复杂，编码时间增加。针对这种情况，现有很多的改进率失真优化算法，可在保证图像质量，码率不会有太大变化的情况下，节省编码时间，减少计算的复杂性。随着人们更进一步的研究，相信在未来几年内，该领域内一定会出现大量的学术研究和成果。

[1]Joint Video Team （JVT）of ISO/IEC MPEG and ITU-T VCEG.H.264|ISO/IEC 14496-10 AVC,Document JVT-G050[S].2003.

[2]WIEGAND T，SULLIVAN G J，BJOTEGAARD G，et al.Overview of the H.264/AVC video coding standard[J].IEEE Trans.Circuits and Systems for Video Technology，2003，7（13）：560-572.

[3]WIEGAND T，SCHWARZ H，JOCH A，et al.Rate-constrained coder control and comparison of video coding standards[J].IEEE Trans.Circuits and Systems for Video Technology，2003，13（7）：688-703.

[4]ORTEGA A，RAMCHANDRAN K.Rate-distortion methods for image and video compression[J].IEEE Signal Processing Magazine，1998，15（11）：23-50.

[5]SULLIVAN G J，WIEGAND T.Rate-distortion optimization for video compression[J].IEEE Signal Processing Magazine，1998，15（11）：74-90.

[6]WIEGAND T，LIGHTSTONE M，MUKHERJEE D，et al.Rate-distortion optimized mode selection for very low bit rate video coding and the emerging H.263 standard[J].IEEE Trans.Circuits and Systems for Video Technology，1996，6（2）：182-190.

[7]WIEGAND T，GIROD B.Lagrange multiplier selection in hybrid video coder control[EB/OL].[2009-09-20].http：//www.asicfpga.com/site_upgrade/asicfpga/pds/image_pds_files/icip01c.pdf.

[8]WU D，PAN F，LIM K P，et al.Fast intermode decision in H.264/AVC video coding[J].IEEE Trans.Circuits and Systems for Video Technology，2005，15（7）：406-409.