摊铺起始时间对组合箱梁沥青摊铺温度场的影响分析
陈 研,陈晓强
(1.南京长江第四大桥建设协调指挥部,南京 210008;2.东南大学,南京 210096)
沥青摊铺是一个短暂的施工过程,所引起的温度场对结构的作用具有时效性,不象日照温度场具有重现性,而且温度场在桥梁纵向上也有所变化。影响结构温度场的因素主要有一天中摊铺起始时间、摊铺季节、桥位处纬度、自然环境条件 (如风速、气温、天气状况)、沥青摊铺厚度和摊铺温度等。由于篇幅所限,本文仅讨论在夏季一天中摊铺起始时间变化对沥青摊铺温度场的影响。对于自然环境条件的影响按不利情况进行考虑,默认风速较小、天气晴朗、空气清晰,让日照作用与沥青高温作用充分地叠加。
1 温度场计算方法及边界条件讨论
任意截面温度变化在时间跨度上分为两阶段:摊铺前和摊铺后。摊铺前,混凝土表面接受太阳照射及与空气之间换热;摊铺后,增加高温沥青部分,混凝土表面转换为内部界面。由于混凝土和沥青材料热量传导缓慢,笔者认为可从纵向上将桥梁切分出有限数量的截面,对每一个横截面单独用横向平面模型来进行温度场计算,以反映出全桥的温度场情况。各截面温度场计算时按两阶段进行,以沥青面层摊铺时刻作为分界点,之前按照日照温度场的计算模型算得温度场,作为摊铺之后的初始温度场[1]。
1.1 太阳辐射
夏季 (林克氏浑浊系数TL=4.0)不同纬度地区水平接受面太阳辐射强度日变化如图1[1,2]所示。高纬度地区正午的辐射强度比低纬度地区的要小10%以内,但日照时间更长;日辐射总量随纬度增加而增大,靠近40度后减小,日辐射总量相差在5%以内。本文计算的太阳辐射强度与文献[3]相比,中高纬度城市建筑物指定的辐射值基本一致,低纬度城市中略小 (9%左右),这是因为南方城市夏季湿度大,大气浑浊度比计算采用的条件(TL=4.0)要大些。
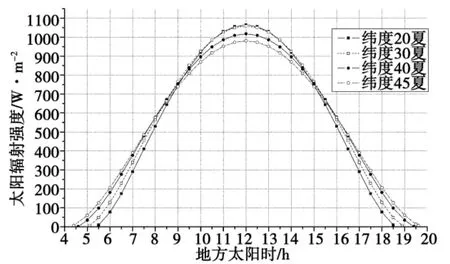
图1 夏季低海拔地区水平接受面太阳辐射强度日变化Fig.1 Daily changes of solar radiation intensity on horizontal surface in the summer of lower altitude
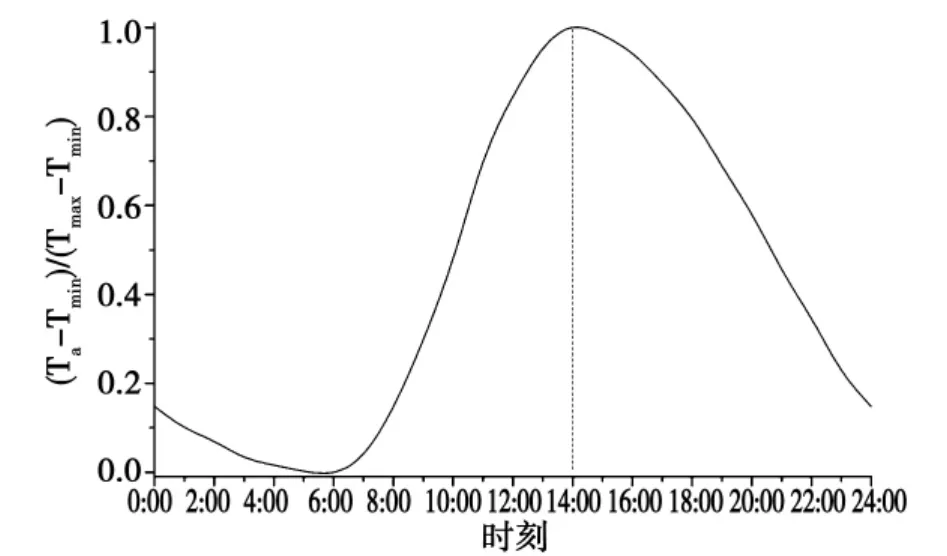
图2 日气温变化标准化曲线Fig.2 Standard curve of daily air temperature change
地面对太阳的辐射,绝大部分被吸收掉,剩余的少部分以漫反射的形式向四周反射,计算时仅对桥面板外侧悬挑、外侧腹板和底板考虑太阳辐射的反射能量,地面平均反射率为0.2。
1.2 大气温度
桥梁结构表面与大气之间进行着对流和辐射换热,在同一风速下,大气温度越低,则结构表面散失的热量越多。每天的气温变化规律,除了某些日子发生天气气候的突变以外,一般都是较为一致的,标准变化曲线[4]如图2所示。文献[2]中列举了60个大中城市夏季最高气温和波幅值,其中绝大部分地区夏季最高温度达到36℃,最大达到40℃,波幅在5.5℃左右。
桥下的空气流动性小,比遮荫气温要略低,而在夜间两者可达到一致的最低气温,因此桥下气温仍按图2进行标准化处理,只是最高气温有所降低,在夏季比气象台最高遮荫气温低1~2℃。
1.3 箱内温度
由于空气导热系数极小,箱内空气与钢箱和混凝土之间主要通过对流换热。箱内空气处于密闭状态,气体流动性取决于箱壁的形状和温度分布情况。在对结构进行复杂的热分析的同时,再考虑箱内气体的流体力学分析,存在边界处理和不同物理场耦合的问题。本文为了回避这些问题,通过试验研究和流体分析[1],按以下过程进行简化处理。
(1)鉴于箱内气温滞后于箱外气温,空气温度的中值与大气遮荫气温的中值相同,波幅值取大气遮荫气温波幅值的一半。钢腹板及底板内壁对流换热系数取 4.74 W/m2·K[5]。
(2)先将上壁面设为绝热条件,按 (1)设置侧、下壁面对流模式,进行计算。
(3)所得某时刻侧、下壁面的平均温度值作为对应时刻的上壁面箱内对流空气温度时变化值,取上壁面与箱内空气之间的对流换热系数为0.5 W/m2·K,重新进行温度场计算。
1.4 空气对流换热
风速越大,则结构表面与空气之间的对流换热越剧烈,则结构温度场的正温差越小,为得到结构不利温度场分布,风速应尽量取小值,一般取1.0 m/s[2]。任意时刻空气与结构上表面的对流换热系数按公式 (1)计算;桥下空气与结构侧表面的对流换热系数取4.74 W/m2·K;由于空气流动性差,与大气接触的桥面板下表面,对流换热系数取2.0 W/m2·K。
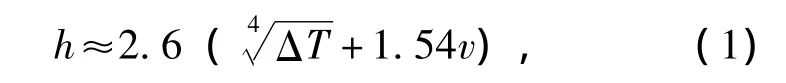
式中:v为风速,v≤5.0 m/s;ΔT为表面温度与周围空气温度之差,以绝对温度计[2]。
2 温度场对结构作用的计算原理

图3 温度自应力计算示意图Fig.3 Calclation schematic diagram of temperature self-stress
非线性温差分布的情况下,梁的变形仍然按平截面假定考虑,对于静定梁式结构,梁在挠曲变形时,因导致截面上的纵向纤维因温差的伸缩将受到约束,从而产生纵向约束应力,称为温度自应力σs。在超静定梁式结构中,还应考虑多余约束阻止结构挠曲产生的温度次内力引起的温度次应力σs。总的温度应力为σt=σ0s+ σs[6]。
2.1 箱梁的温度自应力
设温度梯度沿梁高按任意曲线T(y)分布,如图3所示,取一单元梁段,当纵向纤维之间不受约束,能自由伸缩时,沿梁高各点的自由变形为:
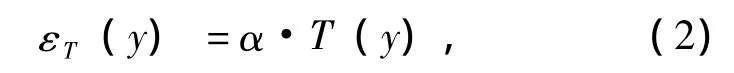
式中:α为混凝土的线膨胀系数。
但因梁的变形必须服从平面假定,所以截面实际变形后,应变为:
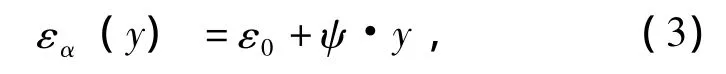
式中:ε0为沿梁y=0处的变形值;ψ为单元梁段挠曲变形后的曲率。
图3中阴影部分的应变,即由纵向纤维之间的约束产生的应变为:
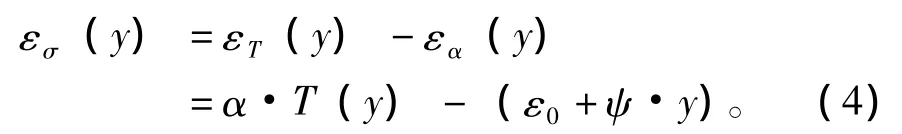
则温度自应力为:
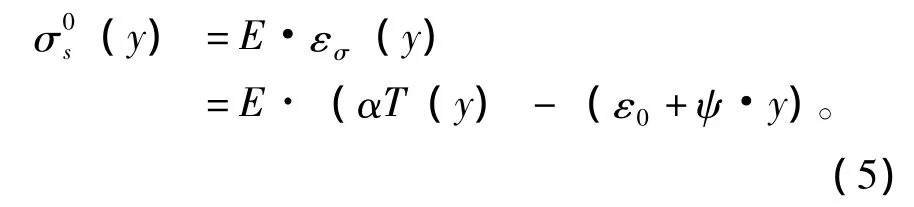
由于在单元梁段上无外荷载作用,可利用截面上应力总和为零和对截面中性轴的力矩为零的条件,求出ε0与ψ值。
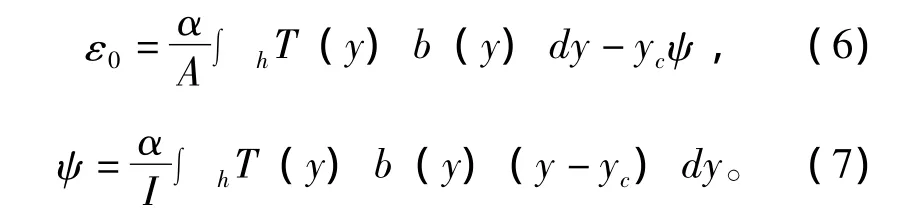
2.2 超静定结构中的温度次内力及其次应力
对于连续梁,曲率ψ将受到超静定赘余约束的制约,引起温度次内力,这可按一般结构力学方法求得,也可按矩阵位移法求解。
公式 (2)~(7)是按匀质材料截面推导的,在计算钢-混凝土组合截面温度应力时,应根据混凝土与钢材的弹性模量进行换算。
3 摊铺时间对沥青摊铺温度场的影响
对于某一个截面,在一天中不同时刻进行沥青摊铺,则之前无沥青铺装时,由混凝土桥面直接吸收太阳辐射能,截面上形成了初始温度场;在沥青高温摊铺后,沥青层中的热量一部分通过大气向外散发,另一部分则向混凝土桥面中进行传递,而且同时沥青层还吸收太阳辐射能,因此存在高温沥青产生的温度场和日照温度场相叠合的过程。为了简化计算分析的过程,先对纵向某一个截面的温度场情况进行分析研究,然后推广至全桥。
3.1 计算条件
计算分析在如下假定条件下进行:
(1)日平均风速为1 m/s,气温在32~37℃,太阳辐射为图1中北纬30°夏季气候条件。
(2)初始时刻为上午5∶00,初始结构温度场为混凝土桥面板均匀32℃,钢箱均匀32℃。持续5 d高温,以达到日照温度场动态平衡 (即温度场稳定周期性变化),第6天进行沥青摊铺。
(3)剪力键数量充足,混凝土桥面板与钢箱之间无滑移,截面变形满足平截面假定。
(4)混凝土强度等级为C50,钢材为16 Mn。
(5)取混凝土、沥青表面太阳辐射吸收系数为 0.65[7,8]和 0.8[9]。混凝土导热系数 1.7 W/m2·K,密度2500 kg/m3,比热容920 J/kg·K;钢材导热系数58.2 W/m2·K,密度7850 kg/m3,比热容480 J/kg·K。
(6)沥青层厚度为6 cm,摊铺温度为140℃。以下分别考虑摊铺时间为6∶00、7∶00、8∶00……18∶00的温度场情况。
根据以上确定的计算参数和边界条件,借助Ansys有限元分析软件进行瞬态热分析[10,11]。计算截面的尺寸如图4所示。分析时采用plane55平面单元对混凝土桥面板及钢箱梁进行建模,为了在同一表面上同时施加太阳辐射热流密度、对流以及辐射换热三种不同的边界条件,在截面外表面上增加表面效应单元 (surf151)。太阳辐射以热流密度的形式施加到表面plane55上,表面与空气的对流换热和辐射换热通过表面效应单元来实现,热流密度、对流及辐射换热的参照点温度均以时间表格数组的形式输入。
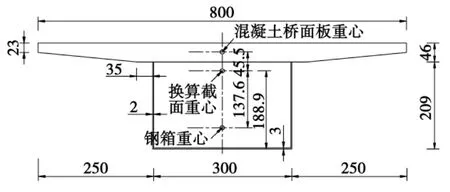
图4 温度场计算截面/cmFig.4 Calculation section of temperature field/cm
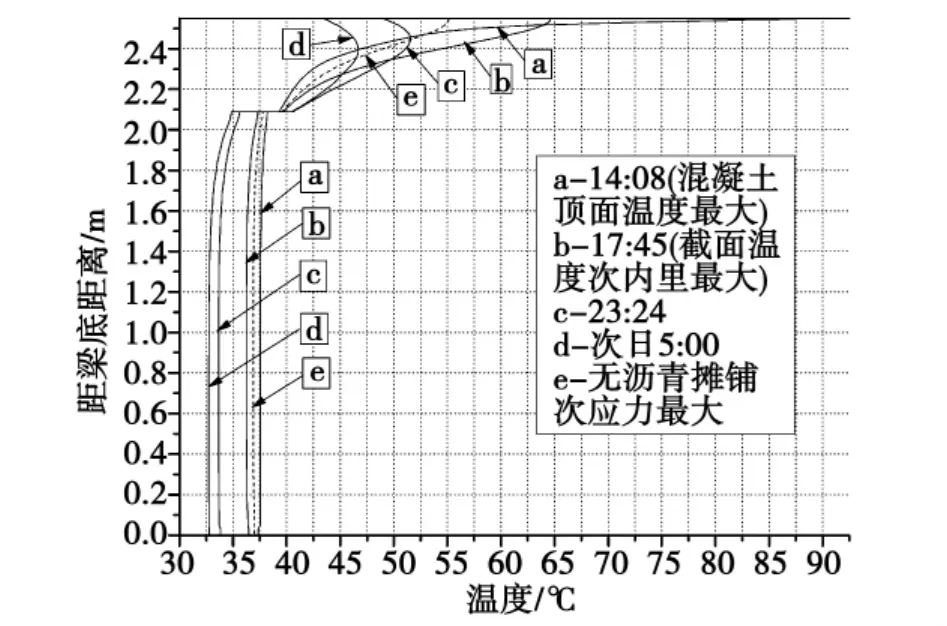
图5 14∶00开始沥青摊铺的温度场Fig.5 Temperature field of asphalt paving from 14∶00
3.2 沥青摊铺温度场特点
14 ∶00 摊铺时截面在不同时刻的理论计算竖向温度场分布如图5所示 (图中e曲线是无沥青铺装最不利日照温差曲线[1])。不同时刻摊铺的混凝土顶面计算温度时程曲线如图6所示。
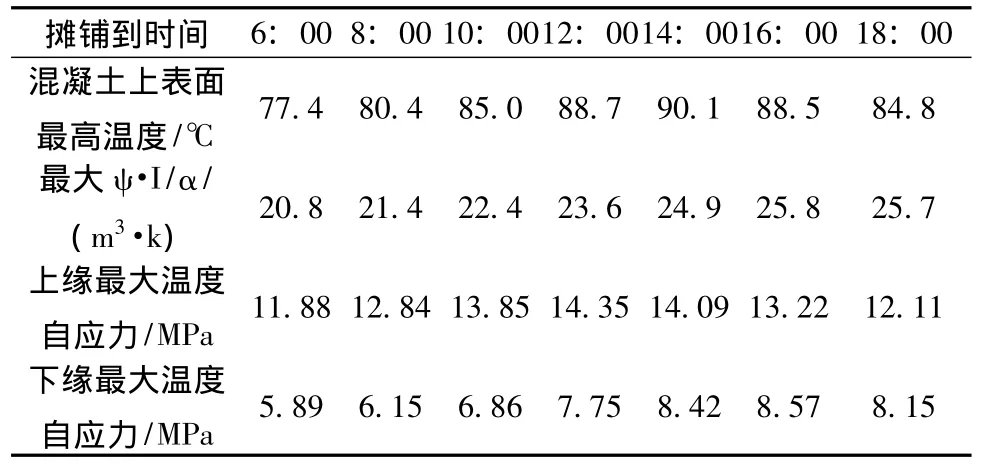
表1 截面温度场情况及上、下缘最大温度自应力Tab.1 Interface temperature conditions and the maximum temperature self-stress in upper and lower edges
由图6、图7及表1可知,截面在摊铺8~15 min内,混凝土桥面板顶面温度迅速达到最大,随后也迅速地降温,速率小于升温速率;在14∶00摊铺时桥面板顶面温度达到最大 (90.1℃),比无沥青摊铺情况下的最高温度高28℃;各截面在摊铺4~9 min内,上缘温度自应力达到最大。
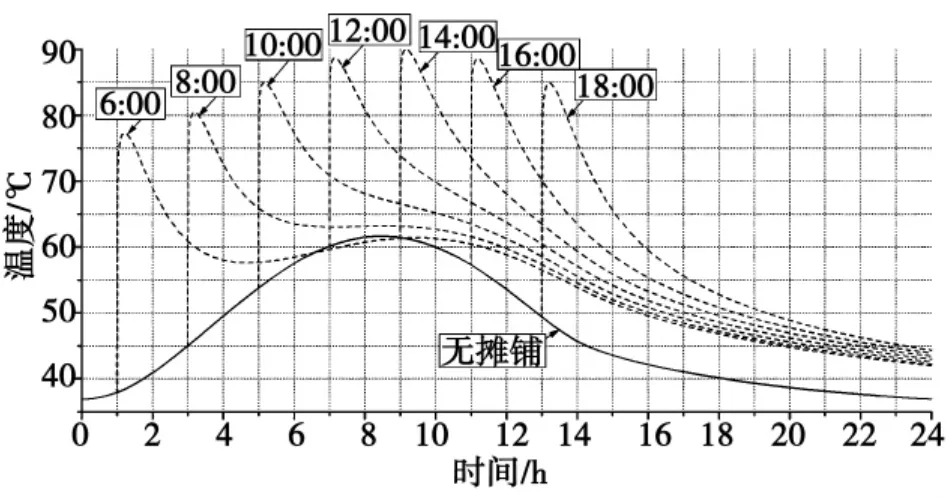
图6 混凝土顶面温度时程曲线Fig.6 Temperature time-history curve on top surface of concrete
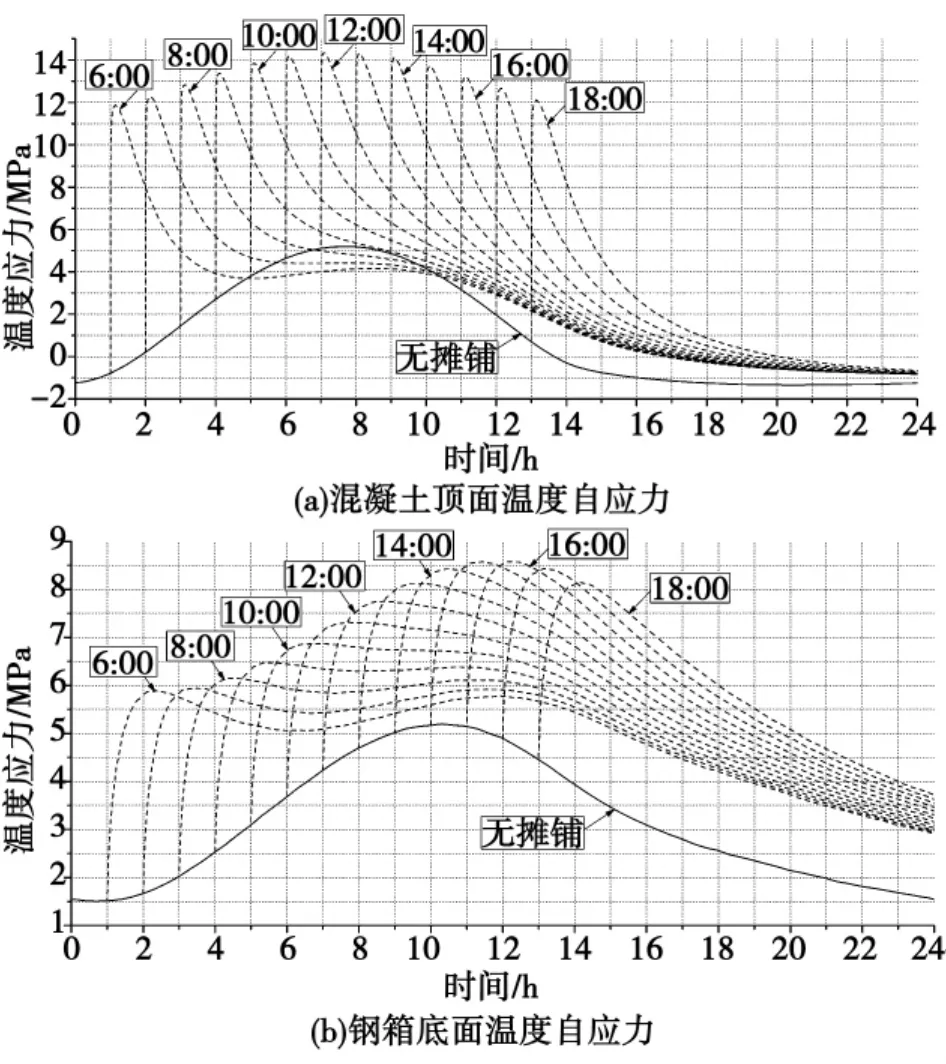
图7 组合截面上、下缘温度自应力时程曲线Fig.7 Time-history curve of temperature self-stress in upper and lower edges of composite section
3.3 温度应力计算方法讨论
各个截面上的温度应力是自应力和次应力的总合,温度自应力只取决于各自截面的温度分布。对于图4的组合截面上、下缘纵桥向温度自应力计算时程曲线如图7所示;而次应力与整个桥跨上的温度场分布 (主要是纵向和竖向两个方向)有关,还与结构的支承条件有关,可以借助某一个截面上的ψ值来反映了次内力作用的强弱[12]。
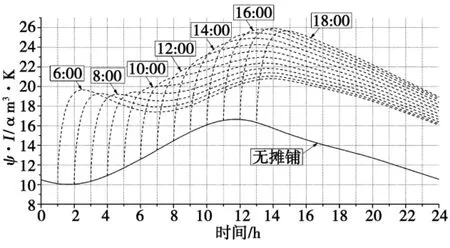
图8 截面ψ时程曲线Fig.8 Time-history curve of section ψ
如图8所示,时间上间隔1 h摊铺的两个截面,在后截面摊铺完1 h之后,两截面的次内力作用相差在5%以内;时间上间隔2 h摊铺的两个截面,在后截面摊铺完1 h之后,次内力作用相差在10%以内,该特点为结构温度次内力的的简化计算创造了条件。在17∶00之前摊铺的截面,最大次内力作用最大时刻基本上在17∶30~19∶00之间,时间越迟,次内力作用越大;在17∶00之后摊铺的截面,摊铺时间越迟,次内力作用越小。
3.4 计算示例
对于跨径布置为30 m+56 m+30 m,截面如图4的桥梁,以2 m/min的速度摊铺,若16∶00时开始摊铺,则17∶00时全桥摊铺完毕。
(1)在19∶00及以后,首铺截面与终铺截面之间ψ·I/α的偏差很小 (5%以内,如图8所示),为此可将17∶00开始摊铺的截面温度场作为全桥的次内力计算温度场,得到跨中截面的温度次应力,再叠加相应时刻的温度自应力,即可得温度总应力 (见表2)。
(2)在19∶00以前,将16∶00开始摊铺的截面温度场作为全桥的次内力计算温度场,得到跨中截面的温度次应力 (结果偏大些),然后再叠加相应时刻的截面温度自应力,即可得到19∶00以前的温度总应力 (见表2)。
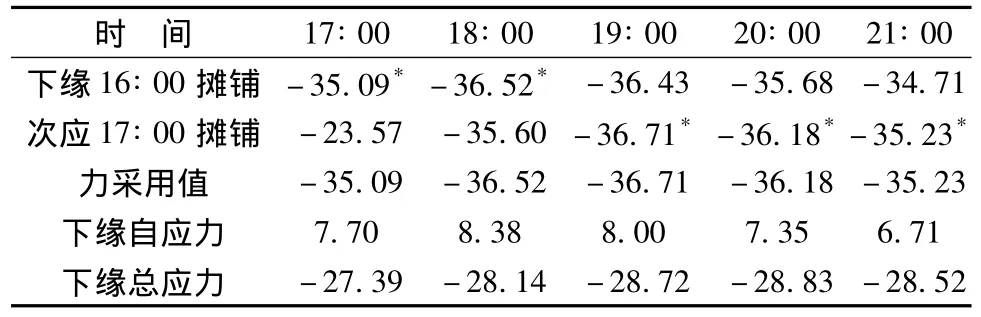
表2 中跨跨中下缘温度应力计算表 (MPa)Tab.2 Table of temperature stress calculation of mid-span section in lower edge
参照以上方法,可得到其它不同时刻开始对全桥摊铺,中跨跨中所达到的最大温度应力,计算结果如下。
(1)白天不管在什么时间 (17∶00之前)开始摊铺,中跨跨中下缘拉应力基本上在19∶00~20∶00达到最大;上缘压应力在该截面摊铺到沥青后5~9 min之内达到最大。
(2)对于混凝土桥面板顶面,摊铺开始时间越早上缘所达到的最大压应力越小,在12∶00摊铺时,上缘压应力达到最大。
(3)一天中摊铺开始时间越早,温度场作用越小,在16∶00开始摊铺,下缘温度场作用最为不利。
4 结论
(1)沥青摊铺阶段,温度场存在时空变化问题,可从纵向上将桥梁切分出有限数量的截面,对每一个横截面单独用横向平面模型来进行温度场计算,以反映出全桥的温度场情况。以沥青面层摊铺时刻作为分界点,之前按照日照温度场的计算模型算得温度场,作为摊铺之后的初始温度场。
(2)截面温度应力是自应力和次应力的总和,自应力取决于各截面的温度分布,而次应力与整个桥跨上的温度场分布有关,还跟结构的支承条件有关。对于连续梁结构,可以借助各截面上的(挠曲变形曲率)来反映次内力作用的大小。
(3)在夏季,一天中摊铺开始时间越早,温度场作用越小,在16∶00开始摊铺时,下缘温度场作用最为不利;对于混凝土桥面板顶面,在中午摊铺时,上缘压应力可达到最大。
[1]陈晓强.钢-混组合连续箱梁桥温度场及温度作用研究[D].南京:东南大学,2009.
[2]F凯尔别克著.刘兴法译.太阳辐射对桥梁结构的影响[M].北京:中国铁道出版社,1981.
[3]中华人民共和国建设部.民用建筑热工设计规范 (GB50176-93)[S].北京:中国计划出版社,1993.
[4]张建荣,周元强,林建萍,等.混凝土结构对流换热效应的研究[J].四川建筑科学研究,2007(3):157-160.
[5]张建荣,刘照球,刘文燕.混凝土表面自然对流换热系数的实验研究[J].四川建筑科学研究,2007(5):143-146.
[6]范立础.预应力混凝土连续梁桥[M].北京:人民交通出版社,2001.
[7]张建荣,徐向东,刘文燕.混凝土表面太阳辐射吸收系数测试研究[J].建筑科学,2006(1):42-45.
[8]Fu H C,Ng S F,Cheung M S.Thermal behavior of composite bridges[J].Journal ofStructural Engineering ASCE,1990,116(12):3302-3323.
[9]韩子东.道路结构温度场研究[D].西安:长安大学,2001.
[10]盛 超,于天来.连续刚构箱梁桥温度场及温度效应的研究[J].森林工程,2008,24(5):49-51.
[11]张朝晖.ANSYS8.0热分析教程与实例解析[M].北京:中国铁道出版社,2005.
[12]周 奇,张 南,许 琦.预应力钢混凝土组合梁预压应力分布研究 [J].公路工程,2008(1):28-31.

