局部多项式回归的图像重建改进

张 明,胡访宇

(中国科学技术大学,安徽合肥230027)

0 引言

图像超分辨率重建 (super-resolution reconstruction,SRR)是指由一幅低分辨率图像或图像序列恢复出高分辨率图像,将获取图像时丢失或降低的高频信息恢复出来的过程。有些文献对SR的定义较窄,只是指基于同一场景的图像序列和视频序列的SRR,实际上,多幅图像的SRR大多数都是以单幅图像的SRR为基础。由于成像系统传感器阵列密度的限制和高昂的成本,SRR技术成为提高图像分辨率的重要方法。在1984年,Tsai和Huang首先提出了基于多幅图像的SRR问题,采用频域方法重建一幅SR图像。此后,研究者们又提出了多种空域方法,如凸集投影法(POCS)、最大后验概率法(MAP)、迭代反投影法(IBP)、最大期望法(EM)等。美国加州大学Milanfar等提出了大量实用SRR算法。本文是在Takeda提出的核函数回归方法进行图像处理和重建[1]基础上,针对像素点随机分布,增加了与像素点数目相关的权重项。

1 局部多项式回归

大小为M×N的灰度图_像可以用_二维函数的观察模型表示。自变量Xi=T,x1i=1,2,…,M,x2i=1,2,…,N。因变量yi是Xi处的像素值,则

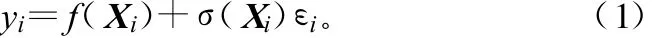
式中,f(◦)为回归函数;σ(Xi)εi是独立同分布零均值方差为σ(Xi)的加性高斯白噪声值,i=1,2,…,P,表示取样窗中像素点数目。

采用不同的基函数都可以将f(◦)展开[2]。X=[x1,x2]T的邻域Xi处的像素值的N阶Taylor展开为:

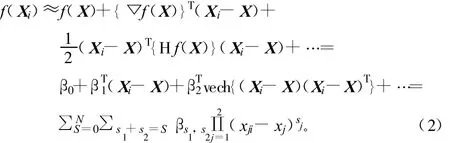
式中,▽和Η分别为梯度算子_和海赛算子;vech(◦)把对称矩阵下三角部分按字典序排成列向量;β0为用回归函数得出的X处的估计值f^(X);{βn}Nn=1为回归函数的n阶梯度系数。

令 β={βs1,s2:s1+s2=S,S=0,…,N},在加权最小二乘下用核函数回归方法求解:

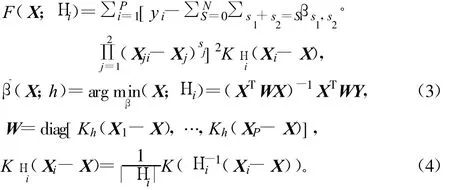
式中,K(◦)代表在中心点处取得最大值的核函数,其限定条件是非负定对称单峰。平滑矩阵 Ηi=hI的求解方法被称为经典核回归(Classical Kernel Regression,CKR)方法。h为全局平滑因子,可以约束取样窗口的带宽,限定取样窗中像素点数目P。h的选定在文献[3]中有进一步的优化,但是计算量比较大。具体推导过程参见文献[4]。

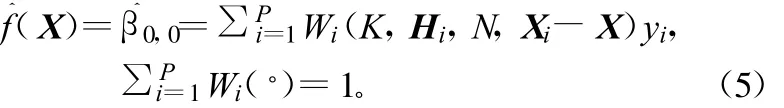
2 改进核回归方法

假设高维空间和低维空间的映射函数是连续平滑的,由Weierstrass估计理论,在低维空间中计算需要重建的像素点和邻域的核函数,并由核函数的线性组合重建高维空间像素点。为获得图像的局部方向信息,假设更精确的平滑矩阵=,梯度向量的协方差矩阵估_计=GTiGi。

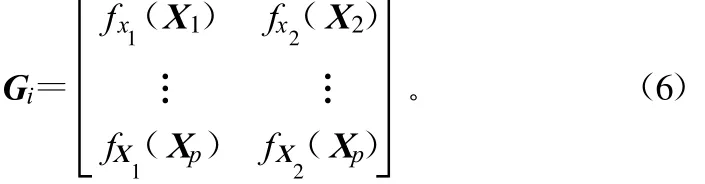
式中,fx1(◦)和fx2(◦)是在x1和x2方向上的梯度;C^i通常是非满秩不稳定的,进行奇异值分解(SVD),处理第一成分和第二成分分量。

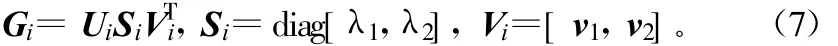
特征向量v1,v2和对应特征值λ1,λ2分别含有图像的局部结构的方向信息和强度信息。

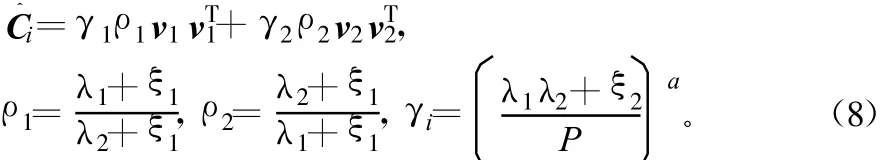
式中,ξi约束缩放因子ρi和尺度因子 γi分母不为零;在图像平坦区域(λ1≈λ2);ρi保持核函数圆形形状,γi步长大 ;在图像边缘(λ1＞ λ2),ρi会沿边缘拉伸核函数的形状,γi步长小。0≤a≤0.5是结构性敏感因子。

这种在CKR的基础上,利用图像的局部方向信息提高重建图像质量的方法称为可控核回归(Steering Kernel Regression,SKR)方法,核函数形式变换如下:

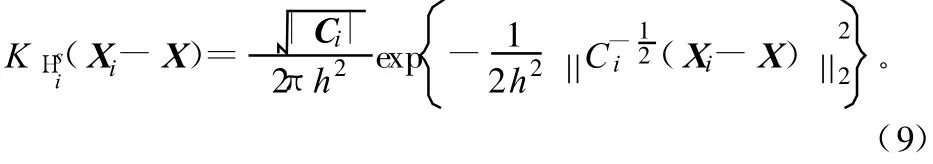
d(Xi , X)=‖ Xi -X ‖22来控制权重大小。考虑到h 一定的情况下, 随机取样像素点数目越多, 则各自的权重应该越小, 改进权重函数因子为:

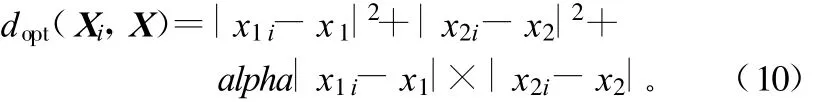
3 实验和结果分析

采用标准测试图像集(512×512)灰度图像,利用随机取样删除85%的像素值。为了保证实验的可重复性和可比较性,设定种子起始状态为0。分别用原来CKR方法和改进CKR方法进行图像重建,利用重建图像的梯度信息运用SKR方法提高图像质量,减小RMSE。

首先,利用lena图像作为测试图像,保持原来CKR方法[1]中设定参数的情况下,在h=2.3时,用原来CKR和SKR方法得RMSE为9.577 dB和8.124 7 dB,用改进 CKR和 SKR方法得RMSE为9.351 9 dB和8.088 9 dB。

h=3时,RMSE随alpha的变化曲线如图1和图2所示。改进CKR方法的RMSE始终下降,改进SKR方法的RMSE先下降,在alpha=1处开始上升。星线对应alpha=0,即原来CKR和SKR方法,各点标出便于比较。改进方法的RMSE曲线始终落在原来方法曲线的下方。

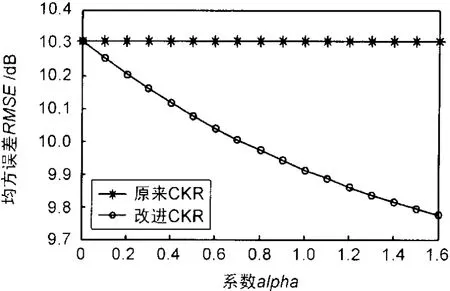
图1 CKR方法的RMSE变化曲线

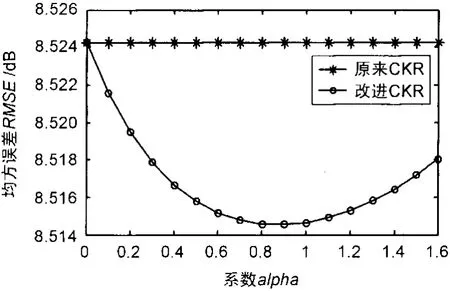
图2 SKR方法的RMSE变化曲线

h=30、alpha=1时,标准测试图像集(512×512)灰度图像数据的实验结果如表1所示。

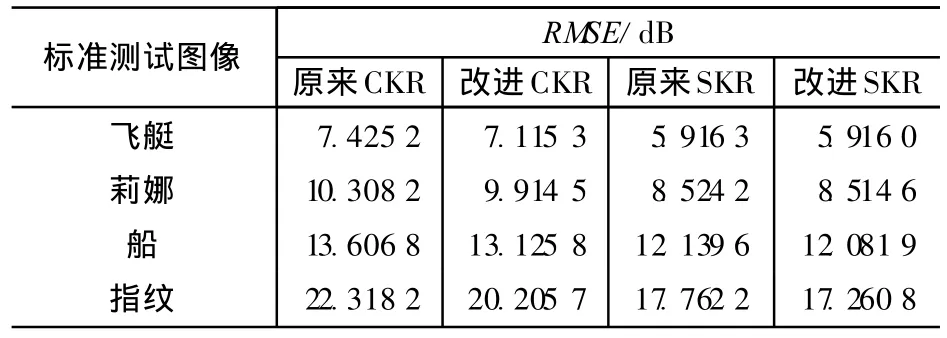
表1 灰度图像数据的仿真结果

4 结束语

在CKR方法基础上考虑权重函数的优化,增加随机取样像素点数目相关的权重项,可以有效降低CKR方法的RMSE。由于SKR方法是利用CKR重建图像的梯度信息进行图像质量的提高,所以改进SKR方法的RMSE降低不会太显著。实验也验证了本方法可以提高图像分辨率,同时降低重建图像的RMSE。

[1]TAKEDA H,FARSIU S,MILANFAR P.Kernel Regression for Image Processing and Reconstruction[J].IEEE Transactions on Image Processing,2007,16(2):349-366.

[2]PHAM T Q,VAN VLIET L J,SCHUTTE K.Robust Fusion of Irregularly Sampled Data Using Adaptive Normalized Convolution[J].EURASIP Journalon Applied Signal Processing,2006(10):1-12.

[3]ZHANG Z G,CHAN S C,ZHANG X,et al.High-resolution Reconstruction of Human Brain MRI Image Based on Local Polynomial Regression[C].IEEE/EMBS Conference on Neural Engineering,April 29-May 2,2009.Antalya,Turkey.NER,2009:245-248.

[4]TAKEDA H.Kernel Regression for Image Processingand Reconstruction[D].Santa Cruz:Univ.of California,2006:32-57.