基于RBF神经网络的自相似业务流预测研究*

欧家成，吴援明

(电子科技大学光电信息学院，成都610054)

1 引言

近年来对局域网和广域网的流量采集和测量表明，网络流量普遍存在自相似或长相关的特性［1］。自相似流量大时间尺度上的突发性会造成网络延迟增加和由于缓冲溢出的失去增大，造成系统资源不必要的浪费。所以网络流量的自相似性给流量控制和网络资源的管理带来了更多的困难，有必要对业务流量作出预测。针对传统的短相关模型在自相似业务分析和预测上的局限性，许多学者根据网络流量的统计特性提出了 FARIMA［2］、小波［3］等数学模型。

相对于复杂的统计模型，神经网络结构简单，并具有自组织、自学习、非线性逼近能力，一些学者提出利用神经网络来解决通信网系统中的一些非线性问题:文献［4］提出用 ARIMA和人工神经网络的组合模型用于流量的短期预测;文献［5］提出一种基于RBF神经网络的网络流量建模与预测。针对通信流量预测的问题，提出用一种简单的径向基(RBF，Radial Basis Function)神经网络预测结构实现自相似业务流的预测，并采用小波方法对数据进行预处理，简化了输入输出关系，提高了预测精度。通过仿真结果与其他预测模型比较，验证了预测结果的精确性和有效性。

2 自相似业务流量的小波预处理

引入极大重叠离散小波变换(MODWT)［6］对数据进行预处理，DWT的计算基于离散紧致集Daubechies小波滤波器。MODWT能够应用于任意大小的样本而且小波系数具有平移不变性，保证了序列具有原始信息一样的有序性和完整性。分别以{gl:l=0，1，...，L －1}和{hl:l=0，1，...，L －1}表示尺度滤波器和小波滤波器，L表示滤波器长度。为了构造 MODWT，重新定义，令cj－1，n=xn，xn为样本序列，j表示分解层数。MODWT塔式算法由{cj－1，n}产生小波系数{dj，n}和尺度系数{cj，n}。

其中，n=1，1，...N －1。在分解层数 j－1 和 j上利用神经网络作逼近会有所不同，因此分解层数j－1上时间序列必须由分解层数j上的序列进行重构。原始信号可以通过逆塔式算法从dj和cj还原得到。

经过预处理的数据在频率成份上比原始流单一，分解后的流量平稳性比原始的流量好得多，有助于简化数据拟合过程。

3 RBF神经网络预测模型

对业务流经过小波分解后，将尺度系数的延迟{cj，n－1，cj，n－2，...，cj，n－q}作为神经网络的输入，q 为神经网络的输入节点数目。网络数据的拟合可以用(4)式来表示。

其中，右边第一项表示网络输出，p为预测步长，ej，n+p为预测值和真实值之间的误差。

3.1 RBF 预测结构

RBF神经网络基本结构如图1所示，隐层为径向基层，输出为一线性层。dist表示取输入向量和权值的欧几里得距离。

图1 RBF网络模型

隐层单元的变换函数是径向基函数，一般用高斯函数作为径向基函数。

网络的隐层单元数目、基函数的中心和权值都需要通过学习决定，采用正交最小二乘(OLS，Orthogonal Least Squares)算法进行网络训练。它是S.Chen［7］等人提出来的，该方法从样本输入中选取数据中心，同时算出输出权值。设 y=［y(1)，y(2)，...，y(N)］T为期望输出序列;隐层输出矩阵为 p= ［p1，p2，...，pM］，其中 pi= ［pi(1)，pi(2)，...，pi(N)］T，1≤i≤M，M 表示隐层神经元数;w=［w1，w2，...，wM］T，为输出权值;E=［ε(1)，ε(2)，...ε(N)］T为学习后误差。将 P 进行奇异值分解P=C×A，A是n×n阶奇异阵。C是N×n阶矩阵且列向量ci是正交的，即CTC=H，H是对角阵，其对角线元素满足基于 OLS解得权值矩阵

确定隐层单元中心的步骤如下:

(1)第一步，令 c1i=pi，对于1≤i≤M 计算

(2)第 k 步，k≥2，对于 1≤i≤M，i≠i1，...，i≠ik－1计算

3.2 RBF网络预测过程

进行自相似业务流量预测的主要思路分为“小波预处理”和“RBF预测”两部分，基本步骤如下:

(1)对业务流量以时间单位进行聚合处理;(2)将数据大小映射到［0，1］之间，选择小波滤波器}和尺度滤波器及分解层数J(本文仿真最大分解层数为2)，根据(1)式和(2)式对1000点数据作MODWT变换;

(3)将变换后的尺度系数构造为神经网络训练样本，训练结束后保存神经网络用作预测结构;

(4)用训练后的RBF神经网络预测训练样本后100点值，并用(3)式进行数据还原。

4 仿真结果

采用Bellcore实验室收集的以太网数据pAug89.TL［8］进行预测研究。首先对数据以时间单位1s进行聚合，选取其中1000点作为样本，将数据大小映射到［0，1］之间，并选择和对样本序列作MODWT变换。将尺度系数作为训练神经网络的输入输出训练样本，仿真中RBF神经网络的输入节点数为20。用训练后的网络预测样本后的100点值。一步预测结果与真实值之间的比较如图2所示。

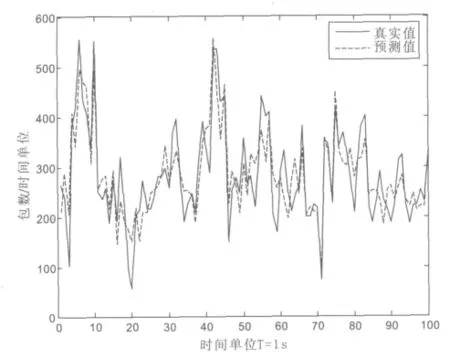
图2 RBF网络一步预测结果与真实值的比较

引入信噪比(SNR，signal to noise ratio)和作为预测性能的评价标准，信噪比越大预测结果越精确。

根据一步预测结果比较了在不同时间尺度下几种不同自相似业务模型的预测性能，这里用作比较的BP神经网络具有三层的10－20－1结构。从表1中可以看出，在不同时间尺度上，网络流量的突发特性仍然不能被平滑掉，具有长相关的性质。RBF预测模型在不同时间尺度上一步预测结果的SNR比AR和FARIMA等数学模型提高了1－2个dB，同BP网络相比有训练过程不受初始值影响，不存在局部极小点的优点，预测结果也更加精确。

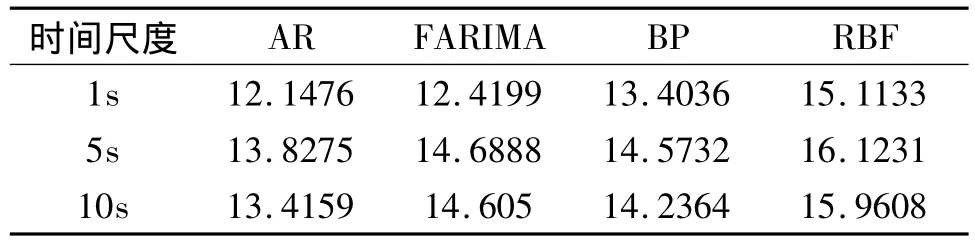
表1 不同预测模型的性能比较

仿照一步预测的实验，用此RBF网络提前五步预测样本之后的100点值，结果如图3所示。

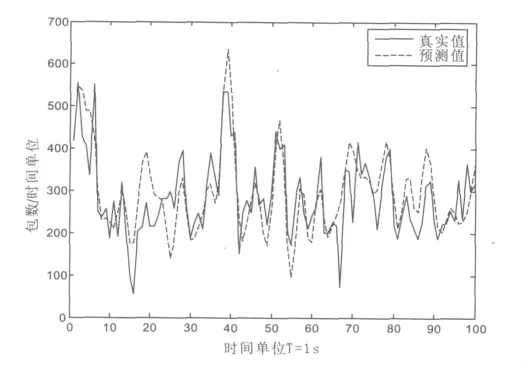
图3 RBF网络提前5步预测结果与真实值间的比较

当预测步长变大时，预测的精度变低。但是此预测方法在多步预测中仍然优于AR和FARIMA等数学模型，这些模型一般预测步长不超过5步时就很快地接近均值了［9］，所以基于小波分解的RBF预测模型在长期预测中仍然有很好的推广性。

5 结束语

提出一种基于MODWT小波预处理的RBF神经网络预测模型，在数据处理中引入了MODWT小波分解，简化了对输入输出关系的拟合，提高了对数据局部信息的跟踪能力和神经网络对数据的处理能力。将RBF神经网络用于自相似业务流的预测研究，采用基于OLS算法的RBF网络，具有结构简单，学习速度快，逼近能力好的优点，能很好地拟合自相似业务流非线性和非平稳的特性。通过仿真比较了在不同时间尺度上一步预测结果的SNR，此预测模型比AR、FARIMA、BP等模型提高了1－2个dB。多步预测的仿真结果说明此预测模型在业务的长期预测中也有很好的推广能力。

［1］W E Leland，M S Taqqu，D V Wilson.On the Self－ similar Nature of Ethernet Traffic［J］.IEE/ACM Transactions on Networking，1994，2(1):1 －15.

［2］Yantai Shu，Zhigang Jin.Traffic Prediction Using FARIMA Models［C］.ICC’99，1999 IEEE International Conference on Communications，1999:891 －895.

［3］Zhang Shuo，Zhao Rongcai，An ke.On Generating Selfsimilar Network Traffic Using Multi－core Processors［C］.2008 International Symposium on Computer Science and Computational Technology.2008:667 －672.

［4］Zeng Dehuai，Xu Jianmin，Liu Liyan.Short Term Traffic Flow Prediction Using Hybrid ARIMA and ANN Models［C］.2008 Workshop on Power Electronics and Intelligent Transportation System.2008:621－625.

［5］王俊松，高志伟.基于RBF神经网络的网络流量建模与预测［J］.计算机工程与应用，2008，44(13):6 －11.

［6］D B Percival，A T Walden.Wavelet Methods for Time Series Analysis［M］.北京:机械工业出版社，2006:159－182.

［7］S Chen，C F N Cowan，P M Grant.Orthogonal Least Squares Learning Algorithm for Radial Basis Function Networks［J］.IEEE Transactions on Neural Networks，1991，2(2):302 －309.

［8］Internet traffic archive［EB/OL］.http://ita.ee.lbl.gov/.

［9］Nayera Sadek.Alireza Khotanzad and Thomas Chen.ATM Dynamic Bandwidth Allocation Using F－ARIMA Prediction Model［C］.The 12th Conference on Computer Communications and Networks.2003:359 －363.