自适应非线性小波在灰度级图像去噪中的应用

胡 欣，张利军

（1.长安大学 电控学院，陕西 西安 710064；2.长城钻探测井公司 国际业务项目部，北京 100101）

1 引言

灰度级图像的信噪比低、边缘模糊、局部空间相关性较强，使灰度图像难以从单一的方法中获得满意的去噪效果，目标局部失真度与图像去噪效果不能达到统一。作为信号处理领域中的一种重要去噪方法，小波变换去相关特性在很大程度上可去除掉图像像素直接相关性，局部时频特性可在小波域维持图像局部几何特性，近年来在图像去噪领域中得到了广泛应用。然而线性小波变换难以描述图像非线性特征。2000年，Heijmans推出了小波与数学形态学理论相结合的形态小波变换，在提升小波框架下提出了非线性小波变换[1-2]，将线性小波变换推广到非线性领域，从而获得对图像边缘和细节较好的保持作用。

线性提升小波构造出的小波基是平滑尺度函数和小波函数[3]，对抑制高斯白噪声较为有效，但图像的失真度大。非线性小波对细节特征的破坏小，但对高斯白噪声的抑制效果差。单一的线性或非线性小波最大的缺点是对所有像素均采用统一的处理方法，为了获得更好的滤波器性能，将线性与非线性自适应地结合，利用图像局部特征自适应地选择更新算子U和预测算子P，从而使更新算子或预测算子与图像数据相关，得到噪声抑制效果好而目标细节保留完整的图像滤波。

笔者在二代小波提升框架下提出一种自适应算法,利用图像的局部特征自适应地选择小波算子，希望在滤除噪声的同时不过多地平滑掉细节信息[4]，通过将线性小波和非线性小波自适应相结合，有效实现了线性小波对高斯白噪声的去除，形态小波对目标细节的保留。实验结果表明，本文方法能有效去除图像的高斯白噪声，减小目标的失真度。

2 形态小波

形态小波兼顾数学形态学的形态滤波特性与小波变换的多分辨力特性，是将小波变换和数学形态学算子相结合的一种非线性小波变换，具有更好的细节保留特性。形态小波中的分析和合成算子需要满足小波变换的一些特性（正交性等），然而算子的选择已不再局限于线性小波算子，而扩展到形态算子。

在二代小波提升框架下，设集合Vj和Wj表示第j级信号空间和第j级细节空间，存在信号分析算子和细节分析算子，存在信号合成算子输入信号 x0∈V0通过分析过程分解为

其中

原始信号x0∈V0通过合成过程精确重建：

提升小波先预测后更新的结构由式（3），（4）构成，预测－更新提升框架的分析、综合算子为

信号x1′和y1′对原始信号x0的重构表示为

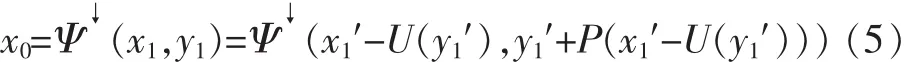
在形态提升小波变换中对原始信号x实现lazy变换，有

将线性小波中的线性算子用非线性形态算子代替，可构成一类非线性形态小波。与线性滤波器加权平均的模糊模型会造成严重的细节损失不同，数学形态学摈弃了传统的数值建模及分析的观点，是作用于物体形状的非线性算子的代数，以上确界 <和下确界 >为基本运算，能够更好地保留图像的细节部分，则一维形态Haar小波取

一维形态Haar小波变换分析算子表示为

一维形态Haar小波的重构运算可表示为

3 自适应提升小波

提升结构是由Sweldens提出的，其中算子P和U都是固定不变的，使实际应用这种结构存在局限性。自适应提升小波变换是根据信号的局部特性来自适应选择预测算子P或者更新算子U，从而得到令人满意的处理效果。

3.1 自适应提升框架

自适应提升框架是由Piella G，Heijmans提出的[5]，本文使用如图1所示的自适应提升框架。

自适应提升框架引入决策参数d控制算子的选取，根据信号的局部特征自适应选取线性和非线性算法，使在侧重保留细节时使用非线性形态小波，在侧重去除噪声时使用线性小波，最优地获取线性小波和非线性小波在图像处理中各自的优点，获得比线性小波和非线性小波更好的结果。由于提升框架是可逆的，自适应变换能够完全重建信号。

3.2 决策信号

定义梯度向量 v（n）=（v1（n），…，vN（n））T∈RN，vj（n）=x（n）-y（n+j），j=-K，…，0，…，N。

二次型半赋范表示为

根据梯度向量本文选取二值函数形式的决策参数

式中：v（n）为梯度向量，p为半范数，T>0为阈值。同时式（12）可写为

若P为真，则[P]=1，否则为0。

4 自适应非线性小波的应用

一维信号中自适应选取小波算法1和小波算法2可实现自适应非线性小波变换。首先实现lazy分解，获取x（n），y（n），计算 dn=D（x，y）（n）=[p（v（n））>T]；当 dn=1 时，采用小波算法1，否则采用小波算法2；得到近似系数x（n）和小波系数 y（n）后，利用阈值来提取疑似目标区域；重构运算得到信号去噪结果。

在自适应提升框架下，笔者提出一种自适应线性小波和非线性小波的提升方法，使在图像去噪过程中获得好的去噪效果同时，不会过多地破坏目标边缘和细节特性。为了验证这种自适应非线性小波算法的有效性和实用性，分别在一维信号和二维图像中进行仿真。

4.1 自适应算法在一维信号去噪中的应用

图2为自适应提升小波算法对信号的一维去噪结果，图2a为不含噪的原始信号，图2b为噪声方差为20的含噪信号，图2c为Haar小波的去噪结果，图2d为db7小波的去噪结果，图2e为形态Haar小波的去噪结果，图2f为自适应算法的去噪结果，其中自适应算法中算法1取形态Haar小波，算法2取Haar小波。

图2c和图2d使用线性小波都不能完全刻画出信号的细节部分，而且db7小波的平滑作用使信号失真。形态Haar小波对目标细节的刻画更加准确，但对噪声的去除不理想。本文提出的自适应形态小波利用自适应参数，在噪声处利用Haar小波去除高斯白噪声的能力，在目标处利用形态Haar小波保留细节的能力，如图2f所示，结合了两种算法的优点达到了更好的去噪效果，证明本文提出的自适应形态小波算法是可行的和有效的。

4.2 自适应算法在二维灰度级图像去噪中的应用

利用二维可分离小波变换，将自适应小波分析在一维所具有的优异特性推广到二维或更高维，可分离的自适应提升小波在灰度图像的去噪算法：

1）分别对图像的每行信号实现一维自适应小波变换；分别对变换后图像的每列信号实现一维自适应小波变换。

2）使用阈值对系数进行阈值处理，提取图像中疑似目标区域。

3）经过重构运算后，得到图像去噪结果。

考虑到算法的实时性和有效性，本文提出了一种自适应算法：小波算法1取形态Haar提升小波，小波算法2取bior2.2提升小波。选取实验的灰度图像长度为200帧，每帧大小为 128×128，图像灰度级是 0～255，实验采用Matlab 7.0.4为软件平台， 阈值 T=Kδ=Kmedian/0.6745，δ为噪声估计方差，ωj，k为原始图像小波变换的小波系数，本文选取文献[6]提出的阈值T=Kδ，取K=3。图3为灰度图像序列的去噪结果。

5 仿真结果及分析

为了说明滤波方法的有效性，引入了信噪比增益和峰值信噪比2个参量来评判滤波质量。信噪比增益（SNR Gain）定义为

式中：（SNR）out是背景抑制后的输出图像信噪比，（SNR）in是输入图像信噪比。峰值信噪比（PSNR）基于图像像素灰度值进行统计和平均计算，是常用的衡量信号失真的指标。尽管对部分图像或视频质量评价时可能与主观感知的质量产生较大的偏差，但PSNR对于多数图像质量仍是有效的[7]，定义为

式中：f（i，j）为不含噪图像，f＾（i，j）为去噪后的图像，图像大小为M×N。

为了分别对目标的局部处理性能进行比较，笔者提出一种新的性能指标参量，称为目标局部峰值信噪比（TPSNR）。TPSNR不同于PSNR，只对目标所在区域的峰值信噪比进行计算，是仅衡量信号中目标信息失真的指标，通过这样的指标能够直观地比较出图像中目标信息的变化，定义为

式中：fT（i）为不含噪信号的目标区域，为去噪后信号的目标区域，信号中目标区域大小为NT。

分别使用db7、形态Haar和本文的自适应算法对3组不同的序列实现去噪处理后，表1为去噪图像的GSNR和TPSNR参数比较。本文提出的自适应形态小波在GSNR上优于形态Haar小波，在TPSNR上优于db7小波。说明本文算法很好地结合了线性小波和非线性的优势，是一种较好的图像去噪方法。

表1 不同提升小波的性能比较

6 小结

在自适应非线性提升框架下，提出自适应非线性提升小波的灰度图像去噪方法，将线性小波和非线性小波自适应地结合起来，有效实现了线性小波对高斯白噪声的去除，形态小波对目标细节的保留，实验结果表明，本文提出的方法能有效去除图像的高斯白噪声，突显图像中的弱小目标。

[1]HEIJMANS HJ.Morphological image operators[M].New York:Academic Press，1994.

[2]GOUTSIAS J,HEIJMANS H J.Multiresolution signal decomposition schemes.Part2： morphological wavelets[EB/OL].[2010-06-01].http：//citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.62.3172&rep=rep1&type=pdf.

[3]吴渝，刘伯红，李刚，等.基于提升方案的自适应小波变换[J].计算机应用研究，2002（6）：18-20.

[4]吴永宏，潘泉，张洪才，等.基于提升框架的一种自适应滤波方法研究[J].电子与信息学报，2005，2（7）：1017-1020.

[5]PIELLA G，HEIJMANS H J.Adaptive lifting schemes with perfect reconstruction[J].IEEE Trans.Signal Processing，2002，50（7）：1620-1630.

[6]DIANI M，CORSINI G，BALDACCI A.Space-time processing for the detection of airborne targets in IR image sequences[J].IEEE Proceedings of Vision， Image and Signal，2001，148（3）：151-157.

[7]佟雨兵，张其善，祁云平.基于PSNR与SSIM联合的图像质量评价模型[J].中国图象图形学报，2006， 11（12）：1758-1763.