直线感应电磁发射器分析与优化

李 献，王秋良，刘建华

(1.中国科学院电工研究所，北京 100190;2.中国科学院研究生院，北京 100190）

直线感应电磁发射器分析与优化

李 献1，2，王秋良1，刘建华1，2

(1.中国科学院电工研究所，北京 100190;2.中国科学院研究生院，北京 100190）

本文对一个两段直线感应电磁发射器进行了分析与优化设计。首先建立了电容驱动的直线感应电磁发射器的数学模型。通过MATLAB编写了系统暂态仿真的仿真程序，给出了系统仿真的流程图。其次比较了直线感应电磁发射器三相电源不同的触发相序对发射性能的影响，得到了最优的触发相序。分析了不同抛体初始位置对出口速度和动能转换效率的影响。最后比较了两段直线感应电磁发射器在第一段电源电压改变时对系统的影响，以及第二段电源电压改变时对系统的影响。从而为下一步的实验提供了理论依据。

直线感应电磁发射器;仿真;出口速度

1 前言

电磁发射器与传统的化学能发射器相比具有效率高，可以获得更大的初速度的优点。美国Sandia实验室在1993年利用一个40级的同步感应线圈炮把400g重的抛体加速到1.1km/s［1］。美国Texas大学为NASA做的一个ETO(earth to orbit）电磁发射装置的初步设计把重量为14kg的物体加速到6km/s［2］。本文对一个两段式的直线感应电磁发射器进行了分析，通过MATLAB编制了仿真程序，对影响直线感应电磁发射器的一些因素进行了比较分析，这为以后的实验提供了依据和理论上的指导。

2 电容驱动的直线感应电磁发射器的数值仿真

直线感应电磁发射器和直线感应电机的工作原理相似。定子驱动线圈串联或并联成多相绕组的连续线圈形式，由多相电源激励，产生一个像异步电动机旋转磁场那样的直线行波磁场，行波速度快于抛体运动速度，借助于其滑差速度引起相对运动，在抛体线圈内感生电流，抛体受到向前的力而加速前进［3，4］。直线感应电磁发射器的供电电源有电容储能，电感储能［5］，飞轮储能［6］。本文中通过不同频率的谐振电容器为两段直线感应电磁器供电。

2.1 电容驱动的直线感应电磁发射器的数学模型

这里采用集中参数的方法建立了电路模型［7］。把铝合金圆筒状的抛体均匀地分为m个圆环。驱动线圈的个数为n。具体的电路模型如图1所示。

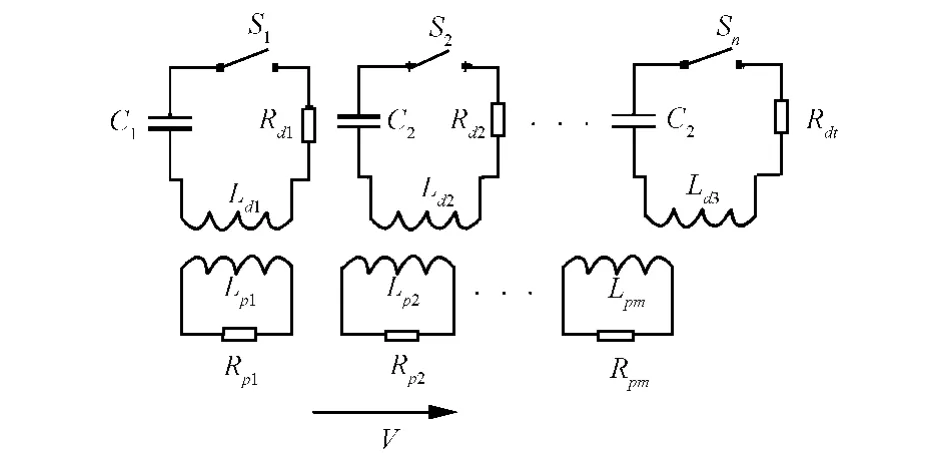
图1 直线感应电磁发射器电路模型Fig.1 Equivalent lumped parameter circuit for linear induction launcher

根据网孔电流分析的方法可以得到以下的电路方程［8］。

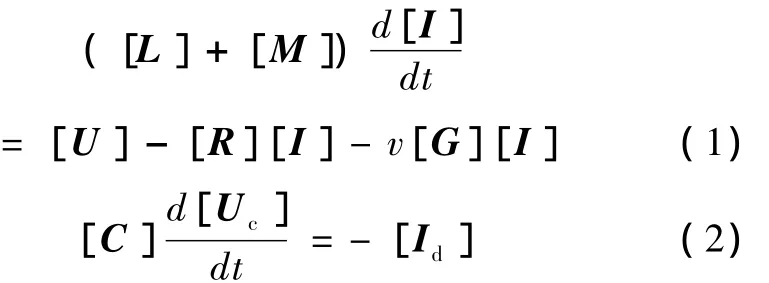
其中

L—驱动线圈和抛体分片的自感，是n+m阶的对角矩阵。

M—驱动线圈和抛体分片的互感，是n+m阶的矩阵。

I=［Id1，Id2…Idn，Ip1，Ip2…Ipm］，是驱动线圈和抛体分片的电流，是个列矢量。

U=［UC1，UC2，…UCn，0，…0］，前 n 项对应是电容电压，后m项是零的列矢量。

R—驱动线圈和抛体分片的电阻，是n+m阶的对角矩阵。

v—抛体的运动速度。

C—是驱动线圈电容容量，是n阶对角矩阵。

同轴感应线圈炮中电枢的受力是驱动线圈和各个抛体分片的总和。与电流和互感梯度的大小有关［9，10］。

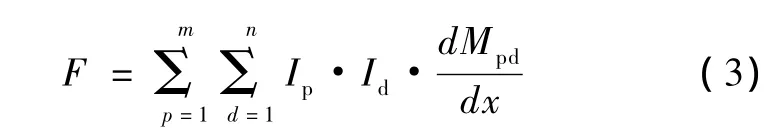
又根据

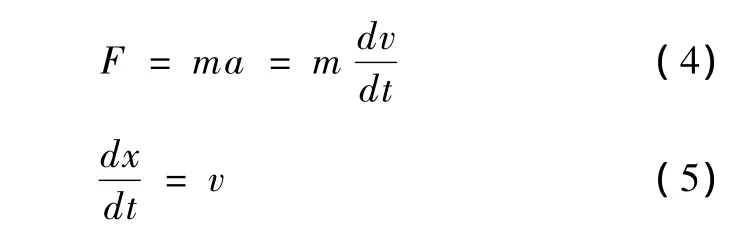
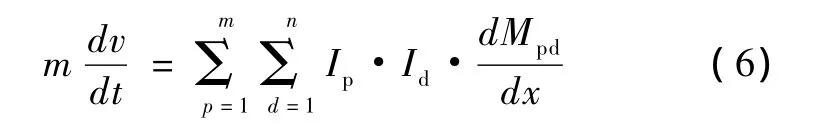
2.2 两段直线感应电磁发射器参数及其数值仿真

线圈参数如表1所示。两段直线感应电磁发射器的电源连接方式如图2所示。

其中a是加速度，v是电枢速度，m是抛体质量，x是位移。

可以得到:

表1 线圈参数Tab.1 Coil parameters

在直线感应电磁发射器的每一段中，几个驱动线圈通过串联或并联形成一相。对于几个驱动线圈串联的情况下，该相电压为几个线圈两端电压的和，该相电流为通过线圈的电流。可以用一个变换矩阵来表示这种关系。

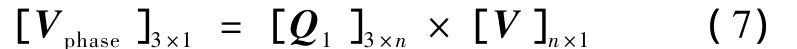
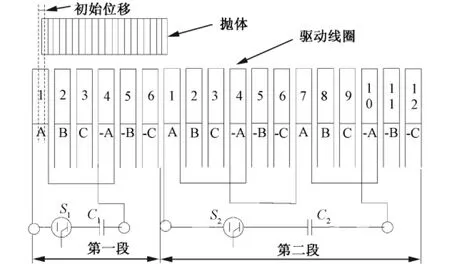
图2 两段直线感应电磁发射器电源中一相的连接方式Fig.2 Terminal connection of one phase of 2 sections linear induction launcher

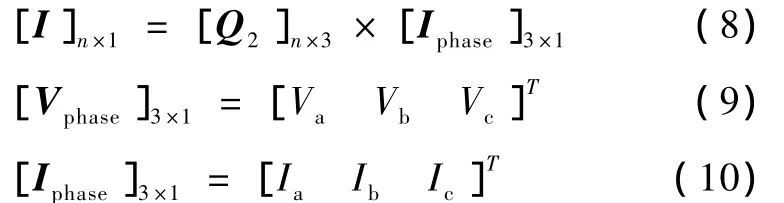
从而公式(1）可以变换为:

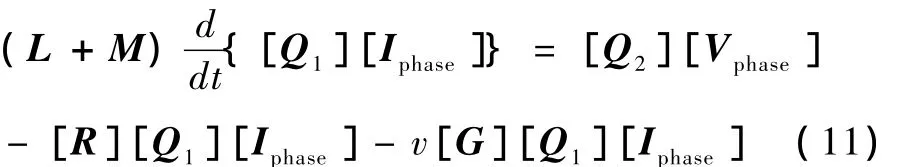
根据变换后的方程式，结合其他的方程可以得到描述整个系统的暂态方程。

利用Matlab编制了两段直线感应电磁发射器的仿真程序。互感，互感梯度采用了 Fawzi法［11］。整个程序的流程图如图3所示。

3 直线感应电磁发射器的设计优化

影响直线感应电磁发射器性能的因素很多，本文对几个主要的方面进行了比较分析。

3.1 三相电源不同触发相序的影响

在这里仅对第一段做了不同触发相序对发射性能的影响，每相电容大小为 C=2200μF，电压大小为U=3.9kV。

图4表示了不同触发相序时位移和速度的关系。曲线 1是 A、-C、B 相序依次相差 30°、60°时位移和速度的曲线;曲线2是相差60°、120°时位移和速度的曲线;曲线3是相差90°、180°时位移和速度的曲线;曲线4是相差120°、240°时位移和速度的曲线。从中可以看出相差 60°、120°时抛体具有最大的出口速度，加速过程平稳。这是一种比较好的相序触发方式。

3.2 抛体不同初始位置的影响

图3 仿真流程图Fig.3 Flow chart of simulation code

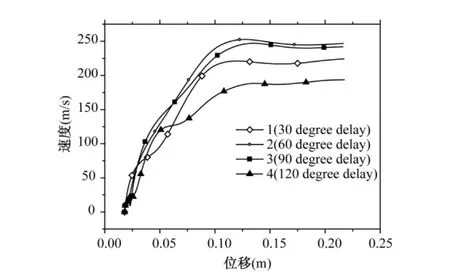
图4 不同触发相序时位移和速度的关系Fig.4 Velocity vs.distance for different firing sequence delay between phases

如图2所示初始位置是指第一个驱动线圈和抛体(分为20个分片）的第一个分片中心之间的距离。在这里仅以第一段为例来比较不同初始触发位置对发射性能的影响。每相电容大小为C=2200μF，电压大小为 U=3.9kV。A、-C、B 相序依次相差 60°、120°。

从表2可以看出，在初始触发位置为0时，系统具有最高的能量转换效率和最大的出口速度。而且在初始位置为4cm时要好于在－4cm时的触发系统。从中也可以看出异步感应线圈炮不必在一个精确时刻触发，在初始位置为0和 －2cm时的效果几乎一样。

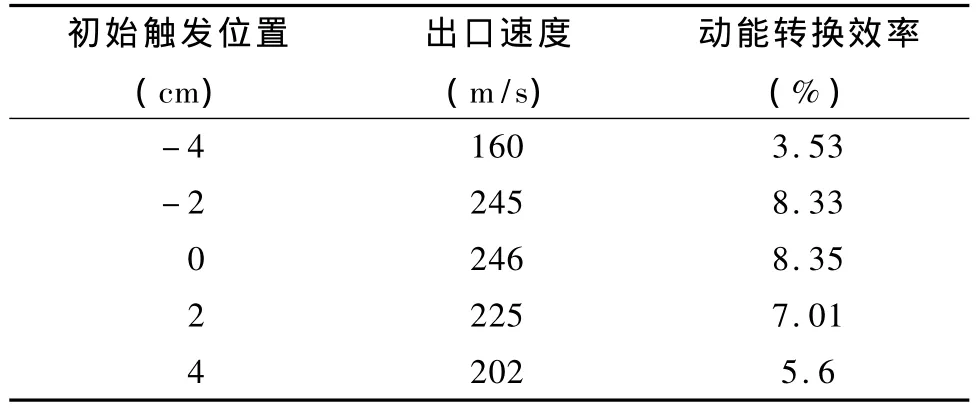
表2 抛体初始触发位置对发射性能影响Tab.2 Effect of initial position of sleeve in first section

3.3 第一段电压改变对发射性能影响

第1段三相电容大小为 C=2200μF。第2段三相电容大小为C=260μF，电压大小为U=15kV。第2段电压保持不变，第1段电压分别为1.8kV、2kV、2.2kV、2.4kV时的位移速度曲线如图5所示。

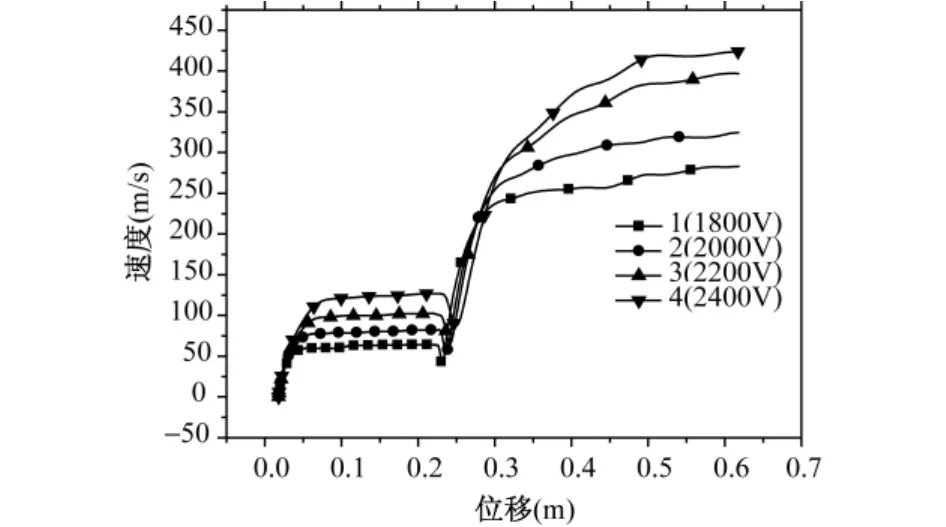
图5 第1段不同电压值时位移和速度的关系Fig.5 Velocity vs.distance for changed voltage in first section

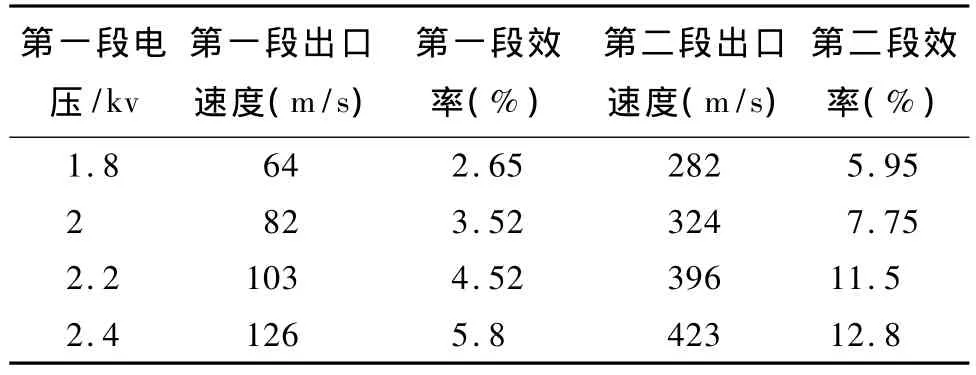
表3 第一段电压改变对发射性能影响Tab.3 Effect of voltage changes in first section

从上面可以看出，第1段电压的改变不仅影响本段的出口速度和能量转换效率，而且对第2段有所影响，随着第1段电压的升高，整个系统的能量转换效率也随着增加。不过如果第一段电压过大会导致在段与段之间的过渡过程中速度下降得过快，影响加速性能。

3.4 第二段电压改变对发射性能影响

第1段三相电容大小为 C=2200μF，电压大小为U=3.9kV。第2段三相电容大小为 C=260μF，电压分别为15kV、17kV、19kV、21kV时的位移速度曲线如图6所示。

图6 第2段不同电压值时位移和速度的关系Fig.6 Velocity vs.distance for changed voltage in second section

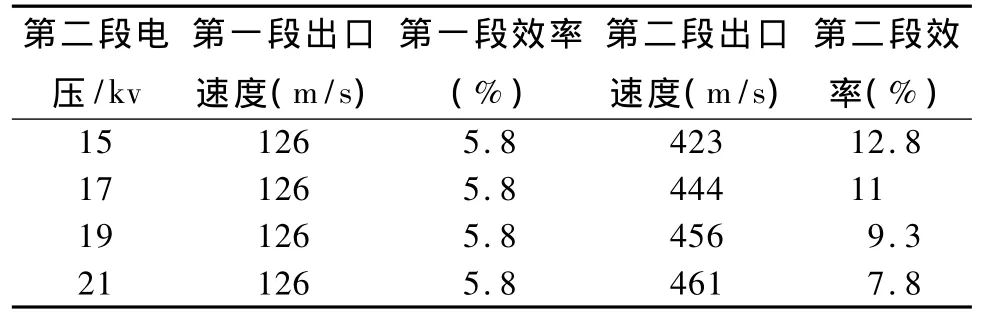
表4 第二段电压改变对发射性能影响Tab.4 Effect of voltage changes in second section

从上面看出，增加第2段的电压，出口速度会有所增加，效率有所减小。如果要获得更高的速度，应该增加驱动线圈的段数。

4 结论

本文建立了电容驱动的三相直线感应电磁发射器的暂态仿真模型，通过MATLAB编制了系统的仿真程序。得到了以下结论。

(1）三相电源 A、－C、B相序依次相差 60°、120°时抛体具有最大的出口速度，这是一种比较好的相序触发方式。

(2）抛体初始位置是0时可以得到最大的出口速度和动能转换效率;

(3）对于两段直线感应电磁发射器来说，第一段电源电压的增加可以提高系统的能量转换效率和出口速度，过大地增加电压会导致段与段之间过渡时速度波动较大;第二段电压增大会导致系统效率的降低，为了得到更高速度，应该增加驱动线圈段数。

References）:

［1］Kaye R J，Cnare E C，Cowan M，et al.Design and performance of Sandia＇s contactless coilgun for 50 mm projectiles［J］.IEEE Trans.on Magnetics，1993，29(1）:680-685.

［2］Driga M D，Weldon W F.Induction launcher design considerations［J］.IEEE Trans.on Magnetics，1989，25(1）:153-8.

［3］Driga M，Weldon W，Woodson H.Electromagnetic induction launchers ［J］. IEEE Trans. on Magnetics，1986，22(6）:1453-1458.

［4］Mongeau P P.Inductively commutated coilguns［J］.IEEE Trans.on Magnetics，1991，27(1）:568-572.

［5］李建辉，刘秀成，王春明 (Li Jianhui，Liu Xiucheng，Wang Chunming）.电感储能型线圈炮系统的建模和参数优化 (Modeling and parameter optimization of coilgun system with inductive energy storage supply）［J］. 电工电能新技术 (Adv.Tech.of Elec.Eng.＆Energy），2007，26(2）:54-58.

［6］Balikci A，Z Zabar，L Birenbaum.Improved energy utilization of linear induction launchers by considering each section as an individual sub-launcher［J］.IEEE Trans.on Magnetics，2009，45(1）:241-243.

［7］He J L，Levi E，Zabar Z，et al.Analysis of inductiontype coilgun performance based on cylindrical current sheet model［J］.IEEE Trans.on Magnetics，1991，27(1）:579-584.

［8］Elliott D G.Mesh-matrix analysis method for electromagnetic launchers［J］.IEEE Trans.on Magnetics，1989，25(1）:164-169.

［9］Lockner T R，Kaye R J，Turman B N.Coilgun technology，status，applications and future directions at Sandia National Laboratories［A］.Proc.26thPower Modulator Symposium and 2004 High-VoltageWorkshop ［C］.2004.119-121.

［10］Wu A Y.Parameter studies for traveling wave coaxial launchers［J］.IEEE Trans.on Magnetics，1991，27(1）:617-622.

［11］Fawzi T H，Burke P E.Accurate computation of self and mutual inductances of circular coils［J］.IEEE Trans.on Power Apparatus and Systems，1978，97(2）:464-468.

Optimization and analysis of linear induction launcher

LI Xian1，2，WANG Qiu-liang1，LIU Jian-hua1，2
(1.Institute of Electrical Engineering，Chinese Academy of Sciences，Beijing 100190，China;2.Graduate University of the Chinese Academy of Sciences，Beijing 100190，China）

In this paper，a two sections linear induction launcher was analyzed and optimized by using computer simulation.Firstly，according to the principles of the mesh-matrix method，a lumped parameter transient model for the analysis of the dynamic conditions was built.The simulation code was programmed by MATLAB.The flow chart for the computer simulation was drawn.Secondly，the effect of varying delay between phases for the 3-phase firing sequence in section 1 was studied and the best time intervals between the firing of the three phases were obtained.It also studied the initial position of sleeve in the first section which affected the muzzle velocity and the kinetic energy transfer efficiency.Finally，the effect of voltage changes in the first section was studied.The muzzle velocity and energy transfer ration was analyzed when the voltage in the second section increased.The computer simulation results have provided a theoretical guidance and experimental basis.

linear induction launcher;simulation;muzzle velocity

TM89

A

1003-3076(2010）02-0043-05

2009-07-28

李 献 (1982-），男，河南籍，博士研究生，主要从事电磁 发射和脉冲功率电源研究;

王秋良 (1965-），男，湖北籍，研究员，博士，主要从事超导磁体及电工电能新技术研究。

book=47,ebook=107