基于实时调度与图分割的汽车网络结构设计研究

王跃飞 韩江洪 张建军 彭 浩

合肥工业大学,合肥,230009

0 引言

随着汽车电子控制单元(electronic control unit,ECU)数量不断增多,汽车网络(如CAN、Flexray)多网段化成为了必然[1-3]。在该结构汽车网络中,将ECU放置到不同网段中会直接影响车辆总体性能和成本。因此,汽车网络结构的设计与优化是整车网络设计需要重点考虑的问题之一[4]。

汽车中与安全密切相关的ECU(如刹车防抱死系统等)对消息传输时间有着严格要求,网络结构设计应该考虑这些时间约束。但目前已有的设计方法主要以降低总线及网关负载为目标,而对网络传输的实时性考虑较少。文献[5]提出了两个网段下CAN总线拓扑设计的多目标优化方法,但没有考虑多网段划分和消息传输实时性要求。文献[6]将单调速率算法应用于混合动力汽车CAN网络的实时性分析,给出了通过调整数据优先级来改善网络实时性的方法,但该方法只适用于单一网段的网络设计。

针对上述方法不足,本文以满足消息传输的可调度性和降低网关负载量为出发点,利用图分割理论和遗传算法建立了汽车网络结构设计方法。该方法可应用在CAN网络及其他汽车网络设计中,具有一定适应性。

1 汽车网络中的实时调度

多网段结构汽车网络由网关和各个网段所组成,如图1所示。同一网段内节点通过网络直接通信,不同网段中的节点通过网关进行交互。为保证消息传输的实时性,需要采用一定的网络调度方法。该类调度方法一般是指应用层调度,与底层网络协议(CAN、LIN)无关,具有较强灵活性和适应性[7]。

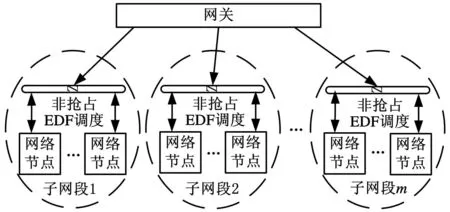
图1 多网段结构汽车网络

图1 所示网络中消息可以分为两类：网段间消息和网段内部消息。其中,网段间消息被节点发送后直接进入到网关内部缓冲队列。设在网关内部针对每个子网段都设置一个虚拟网络服务器(virtual network server,VNS),负责内部缓冲队列中消息的发送。每个VNS都是一个总带宽服务器(total bandwidth server),运行机制如图2所示[8]。在网段内部,各个节点中的消息与VNS一起采用非抢占最早时限优先(earliest deadline first,EDF)算法调度。

图2 VNS的预算补充和时限设置

网络中任何消息均可用三元组(t c,T,t D)表示,其中,tc为消息的网络传输时间,T为消息的传输周期,t D为消息的相对传输时限,且T=t D。任意 VNS 用二元组(˜u,es)表示,其中 ,˜u为 VNS的规模,e s为它的执行预算。设n为网络中网段的数目,Mi={m1,m2,…,mr}为网段i中节点发送消息集合,Mgi={m1,m2,…,mh}为网关内网段i所对应缓冲队列中的消息集合,α为网络传输能力,它等于实际网络带宽与标准网络带宽的比值。

定理 对于任意网段i,假设集合Mgi中消息在网络传输能力αi(αi≤1)的实际网络中是可调度的,如果存在˜ui=αi且式(1)成立,则图1所示的网络中消息一定能满足其传输时限,即都是可调度的。

证明 对于任意网段i,网络中消息分别来自内部节点和网关。从调度角度来看,如果把对应的VNS看成一个非周期消息,则该消息与节点消息只要满足非抢占EDF算法的可调度条件,就可保证VNS与节点消息的时限;但是对于网关内消息而言,仅能保证其VNS可调度是不够的,还需要保证消息在VNS内部可调度。

由文献[8]推论可知：如果式(1)成立,节点消息与规模为˜ui的VNS在非抢占EDF算法下都是可络传输不可抢占性带来的影响,els/˜ui实际上是第i个VNS的时限。分析式(1)可知,当其成立时,必有˜ui≤1,同时,M g i中所有消息在网络传输能力αi(αi≤1)的实际网络中是可调度的,且˜ui=αi。根据上述推理结果,仿照文献[9]定理3证明过程可以推出M g i中的消息也是可调度的。

因网段i为任意网段,故已知条件成立时,网络中所有消息都是可调度的。

证毕。

2 网段划分的图分割模型

在汽车网络结构设计时,将不同的节点放入不同的网段,对网络负载量和消息传输实时性有着直接的影响。因此,在网段划分时需要综合考虑网络负载量和消息传输实时性两方面的约束,具体可按以下原则进行划分：

(1)将相互间通信量较大的节点尽量分配到同一网段中,以降低不同网段间消息传输的转发时间,减轻网关负担。

(2)对网段内部节点通信量进行限制,以保持各网段负载均衡,避免悬殊过大。

(3)保证网络中消息的可调度性,确保在其时限内完成传送。

设汽车网络中具有n个节点,每个节点周期性地向总线发送数据。对于多网段结构的汽车网络可以用图分割模型来描述[10-11]。定义无向图：

G={V,E,W}

式中,V为汽车网络节点集合,V={v1,v2,…,vn};E为节点间的相互通信关系,E={e1,e2,…,ek};W为G边上的权值集合,W={wij};wij为节点vi与节点vj之间的通信量,令 wii=0。

汽车网络划分实际上可以看成子图划分问题,即在满足一定条件下将集合V分解成m个无交集的子集V1,V2,…,Vm,即

根据网络划分原则,子图划分就是在保证各网段可调度的基础上,实现子图间流量最小化和各子图负载均衡。因此可以建立如下目标优化模型：

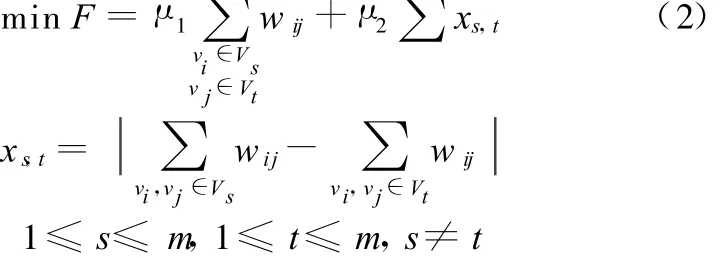
式中,μ1、μ2为权重因子,有 μ1+μ2=1。

约束条件：

式(2)的目标函数由两部分组成,第1部分表示子图间流量,第2部分表示各子图内部负载的差异,它们分别与网段划分原则(1)和原则(2)对应。而式(3)表示子图中节点消息传输可调度的条件,与原则(3)对应。

上述优化问题实际上属于NP完全问题,采用遗传算法(GA)求解是较好的选择。本文引入参数自适应策略来扩大搜索空间,引入小生境策略创造小生境进化环境,维持群体多样性,建立了小生境自适应遗传算法(niched adapative genetic algorithm,NAGA)[11-12]。算法步骤如下：

(1)编码方法。本文采用符号编码方式。假设网络中共有n个网络节点,划分的子图数为m个,则编码长度为n的编码串x=(λ1,λ2,…,λn)表示问题的一个解,其中λi=q表示第i个节点分配至第q个子图中。

(2)适应度函数。本文采用由解空间中某一点的目标函数F(x)到搜索空间相应个体适应度函数值转换的方法。即适应度函数为

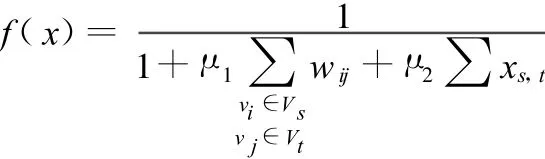
(3)遗传算子。为了简化操作过程,本文采用比例选择算子,对于交叉和变异操作分别采用单点交叉操作和简单对换变异操作。

(4)染色体有效性验证。为保证进化中染色体满足式(3)的约束条件,在交叉和变异操作后必须对染色体进行有效性验证。通过验证的个体为合法染色体;反之为非法染色体,需重新进行相关遗传操作。

(5)控制参数的动态调整。采用自适应策略来动态调整交叉概率Pc和变异概率Pm。设偏差δ分别为某一代种群中最大个体适应度和个体平均适应度值。当δ较小时,种群趋向早熟,应该增大 Pc、Pm;而当 δ较大时,种群早熟不显著,为提高搜索速度可以减小

(6)小生境计算。为维护群体多样性,使得最优个体在约束空间中分散开来,需要计算个体间的海明距离[11];在该距离内,适应度小的个体降低适应度,增加被淘汰的机率。

(7)终止条件。当前代数达到设定最大代数或个体适应度连续若干次未发生增长时终止算法。

4 设计方法的应用

国内某自主品牌汽车的一款车型配置包括发动机ECU、自动变速箱ECU、汽车空调ECU、安全气囊ECU、组合仪表ECU、车身ECU和电动助力等多个电子系统。

设其网络中ECU数目为20个,拟划分为3个网段。汽车网络使用CAN总线,通信协议采用Bosch CAN2.0B,数据帧采用标准CAN数据帧,CAN网络带宽为125kbit/s,节点消息的相关参数如表1所示。如果节点间通信量用单位时间内各节点发送的消息数量来表示,则节点通信矩阵为

表1 各节点消息的相关参数

为验证所提出的方法,分别采用普通遗传算法和本文NAGA算法对该网络划分问题进行了求解。设定群体规模均为100,GA的交叉概率为0.9,变异概率为0.05,NAGA的初始交叉概率和变异概率也分别为0.9和0.05。

求解过程中个体适应度和目标函数变化如图3和图4所示。从图3和图4看出：GA在进化到50代时开始收敛,最大的个体适应度值为0.032 143,目标函数最小值为30.20;NAGA在进化到85代时开始收敛,最大的个体适应度值为0.035 651,目标函数最小值为 27.05。同时NAGA所获得最优个体的数目也远多于GA。这说明小生境策略和参数自适应策略的引入,扩大了NAGA的搜索空间,避免了早熟现象,所获得解的质量要优于GA获得结果。

选取NAGA优化过程中10个最优个体,按照目标函数从大到小顺序排列得到的结果如表2所示 。 如果网关内各 VNS 的规模 ˜u1 、˜u2 、˜u3 均等于0.25,通过计算可知,所有染色体均能满足式(3)。这说明所获得的网段划分方案能够确保消息传输的网络可调度要求。

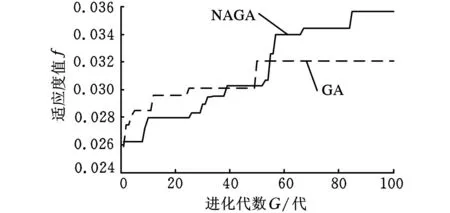
图3 适应度函数f的优化过程

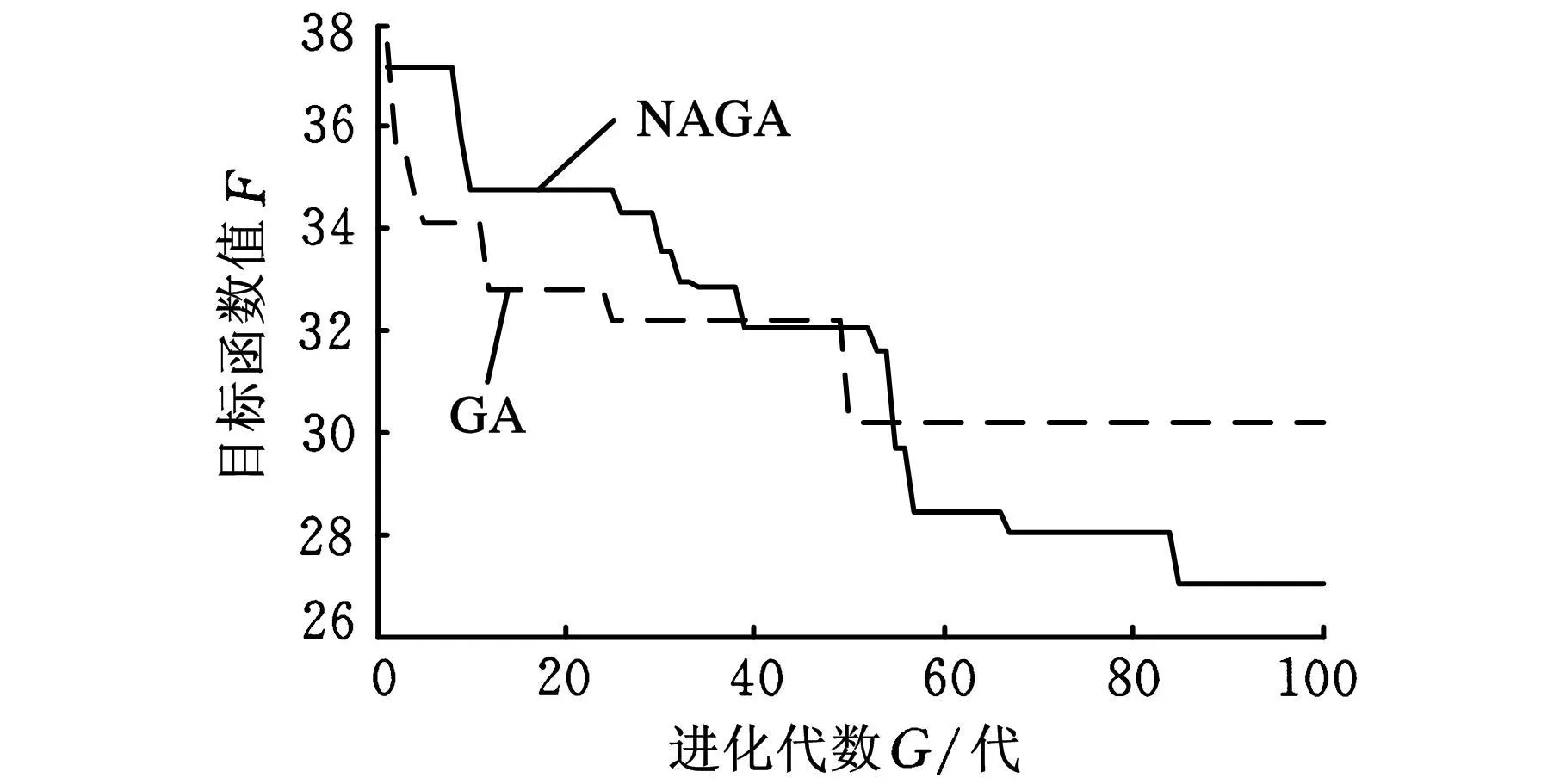
图4 目标函数F的优化过程

为得到最优网络结构,需进一步分析该10个方案。根据网段划分原则(1),即尽量减小子网间的通信量,显然方案 5、方案 7、方案 8、方案 9和方案10符合要求。考虑到划分原则(2),即保持各子网负载均衡,方案5、方案8和方案10是更可取的方案。对比这3个方案,由于方案10的目标函数值最小,故方案10为最佳方案。即将20个节点按照以下方式划分到3个网段中(括号中数字为各节点的节点号)：网段1：(9,10,11,12,15,20),网段 2：(1,2,3,7,8,13,18),网段 3：(4,5,6,14,16,17,19)。

表2 NAGA求解结果分析

4 结语

汽车网络结构设计问题本质上属于多目标优化问题,在实际设计中需要考虑多方面的约束。其中,网络负载率和传输实时性是两个需要重点考虑的因素,它们直接关系到消息传输的安全性和可靠性。本文以满足消息可调度性和降低网段间通信量为出发点,采用图分割模型来描述网络划分问题,建立了汽车网络结构优化设计方法。这种方法降低了网络结构分析与设计的难度,为建立多目标约束下的汽车网络结构设计方法进行了有益的探索和尝试。

[1] Li Renjun,Liu Chu.Design for Automotive CAN Bus Monitoring System[C]//IEEE Vehicle Power and Propulsion Conference.Harbin：IEEE,2008：1-5.

[2] 胡建军,赵玉省,秦大同.基于CAN通信的混合动力系统硬件在环仿真实验[J].中国机械工程,2008,19(3)：300-304.

[3] Luo Feng,Chen Zhiqi.Research on Flexray Communication System[C]//IEEE Vehicle Power and Propulsion Conference.Harbin：IEEE,2008：4547-4550.

[4] Navet N,Song Y.Trends in Automotive Communication Systems[J].Proceedings of the IEEE,2005,93(6)：1204-1223.

[5] 曲凤丽.汽车网络研究及CAN总线网络拓扑的优化[D].杭州：浙江大学,2008.

[6] 李稚博,张俊智,卢青春.混合动力电动汽车车上CAN网络设计实时性分析[J].汽车工程,2005,27(1)：16-19.

[7] 岳东,彭晨,Qinglong Han.网络控制系统分析与综合[M].北京：科学出版社,2007.

[8] Liu J W S.Real-time Systems[M].Upper Saddle River,New Jersey：Prentice Hall,2003.

[9] Deng Z,Liu J W S.A Scheme for Scheduling Hard Real-time Applications in Open System Environment[C]//Euromicro Workshop on Real-time Systems.Toledo,1997：191-199.

[10] 陈国龙.基于遗传算法的计算机通信网的拓扑优化设计[J].计算机科学,2002,29(11)：141-143.

[11] Han Jianghong,Wang Yuefei,Hou Zhengfeng,et al.An Approach of Industrial Ethernet Network System Design with Hybrid Niche Genetic Algorithm[C]//World Congress on Intelligent Control and Automation.Dalian：IEEE,2006：3699-3703.

[12] 于兰峰,王金诺.基于遗传算法和神经网络的塔机结构动态优化设计[J].中国机械工程,2008,19(1)：61-63.