双色噪声驱动的光学双稳系统动力学行为研究
(长江大学物理与科学技术学院,湖北 荆州 434023)
系统的噪声及其关联形式对非线性系统有很大的影响[1~7]。为了简化计算,在对噪声的处理上,常把记忆时间或者宽带很短的激励视为白噪声,但真正的白噪声并不存在。最近,非白噪声驱动非线性系统性质的研究工作受到了人们的广泛关注,文献[8]研究了信号调制色泵噪声和实虚部间关联量子噪声驱动下单模激光的随机共振现象,文献[9]研究了色噪声驱动的非对称双稳系统的平均首次穿越时间,文献[10]研究了双色噪声驱动非对称双稳系统平均第一穿越时间。而双色噪声驱动的光学双稳系统的研究尚未报道,研究该系统的动力学行为可以为提高光学双稳系统的输出效率提供理论依据。为此,笔者讨论了抽运噪声和量子噪声均为色噪声情况下的光学双稳系统的输出信噪比,并具体分析了抽运噪声强度P、量子噪声强度Q、抽运噪声自关联时间τ1和量子噪声自关联时间τ2对输出信噪比R的影响。
1 信号调制的光学双稳系统的相关函数
考虑有信号调制抽运噪声的一维过阻尼双稳系统,该系统可由以下光强方程描述[11]:
(1)
该系统的统计特性由其均值和方差给出:

(2)
式中,I为光强;ξ(t)为抽运噪声;η(t)为量子噪声;P为抽运噪声强度;Q为量子噪声强度;τ1为抽运噪声自关联时间;τ2为量子噪声自关联时间;B为调制信号强度;Ω为调制信号频率;c为双稳参数。
将式(1)在定态光强I0附近线性化。令I=I0+δ(t′),得线性化方程为:
(3)
(4)
稳态平均光强关联函数为[6]:
(5)
对式(5)作傅里叶变换可得到输出光强的功率谱为:
S(ω)=S1(ω)+S2(ω)
(6)
式中,S1(ω)为输出信号功率谱;S2(ω)为输出噪声功率谱。
输出功率的信噪比定义为输出信号总功率与ω=Ω处的单位噪声谱的平均功率之比:
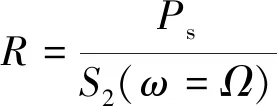
(7)
其中:
代入式(7)得到输出光强信噪比为:
(8)
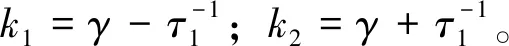
2 各因素对信噪比的影响研究
2.1 信噪比R随抽运噪声自关联时间τ1的随机共振
根据式(8),可以绘出以量子噪声自关联时间τ2为参数信噪比R随抽运噪声自关联时间τ1的变化曲线(P=0.01,Q=0.005,Ω=20,B=5,c=10,I0=10),如图1。由图1可以发现:①信噪比R先随抽运噪声自关联时间τ1的增大而增大,达到极大值后,又随抽运噪声自关联时间τ1的增大而减小,表明信噪比R随着抽运噪声自关联时间τ1的变化系统有随机共振现象;②量子噪声自关联时间τ2对系统的随机共振现象有较大的影响,随着量子噪声自关联时间τ2的增大,R-τ1曲线整体上移,共振峰值增高,峰值位置右移,表明延长量子噪声自关联τ2时间可以增加输出光强信噪比R的共振强度。
2.2 信噪比R随双稳参数c的变化
选择抽运噪声自关联时间τ1为参数可描绘出信噪比R随双稳参数c的变化曲线(P=0.01,Q=0.005,Ω=20,B=5,τ2=0.001,I0=10),如图2。由图2可以看出:①当双稳参数c增加时,信噪比R先增大后减小,即输出光强信噪比R出现极大值;②抽运噪声自关联时间τ1对系统的输出信噪比R影响较大,随着抽运噪声自关联时间τ1的增大,峰值降低且位置左移,R-c曲线变平坦,表明缩短抽运噪声自关联时间τ1可以增大输出光强信噪比R。
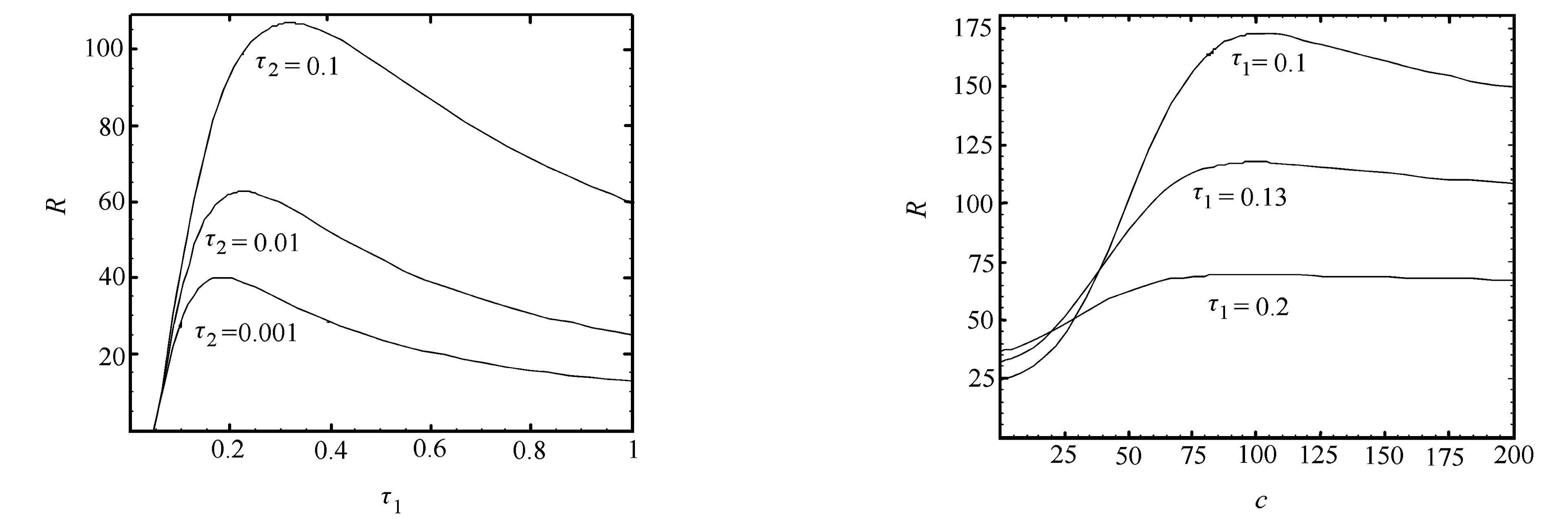
图1 信噪比R以量子噪声自关联时间τ2 图2 信噪比R随双稳参数c的变化曲线为参数随τ1的变化曲线
2.3 信噪比R随抽运噪声强度P的变化
以量子噪声强度Q为参数时信噪比R随抽运噪声强度P的变化曲线(B=5,Ω=20,τ1=0.1,τ2=0.001,c=10,I0=10)如图3所示。从图3可以看出:①信噪比R随抽运噪声强度P的增大而单调递增,最后趋于饱和;②随着量子噪声强度Q的增大,R-P曲线整体下移,但当抽运噪声强度P很大时,对应不同量子噪声强度Q的值信噪比R会趋于一个定值,表明增大抽运噪声强度P、减小量子噪声强度Q均可以增大输出光强的信噪比。
2.4 信噪比R随量子噪声强度Q的变化
以抽运噪声强度P为参数时信噪比R随量子噪声强度Q的变化曲线(B=5,Ω=20,τ1=0.1,τ2=0.001,c=10,I0=10)如图4所示。从图4可以看出:①信噪比R随量子噪声强度Q的增大单调递减;②随抽运噪声强度P的增大,R-Q曲线整体上移。可见抽运噪声强度P和量子噪声强度Q对输出信噪比R的影响并不相同。
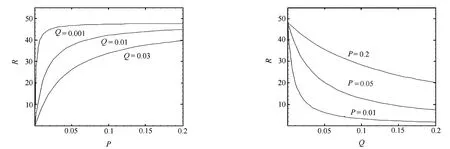
图3 信噪比R随抽运噪声强度P的变化曲线 图4 信噪比R随量子噪声强度Q的变化曲线
3 结 论
综上所述,在色抽运噪声和色量子噪声驱动的光学双稳系统中,通过讨论抽运噪声强度P、量子噪声强度Q、抽运噪声自关联时间τ1和量子噪声自关联时间τ2对输出光强信噪比R的影响,可以得到如下结果:①信噪比R随抽运噪声自关联时间τ1的变化过程中存在随机共振现象,而量子噪声自关联时间τ2对随机共振存在较大的影响,当τ2增加时,R-τ1曲线整体上移,峰值增大,表明延长量子噪声自关联时间可以增加输出光强信噪比的共振强度。②信噪比R随双稳参数c的变化过程中有一个极大值,抽运噪声自关联时间τ1对R-c曲线有较大的影响,随着τ1的增大,R-c曲线的极大值降低且变平坦,表明缩短抽运噪声自关联时间可以增大输出光强信噪比。③信噪比R随抽运噪声强度P变化单调递增,随量子噪声强度Q变化单调递减,因此,可以增大P或减小Q以获得较大的输出信噪比。
[1]Cheng Qing-Hua,Cao Li,Xu Da-Hai,etal.Time evllution of the intensity correlation function in a single-mode laser driven by both the coloured pump noise with signal modulation and the quantum noise with cross-correlation between the real and imagenary parts[J].J Chin Phys Soc,2005,14(6):1159~1167.
[2]Fulinski A,Gora P F.Universal character of Stochastic resonance and a constructive role of white noise[J].J Stat Phys,1999,101:483.
[3]Berdichevsky V,Gitterman M.Stochastic resonance and rechets2new manifestations[J].Europ hys Lett,1996,36:161~167.
[4]Zhang Liangying,Cao Li,Wu Dajin,etal.Stochastic resonance in linear regime of a single-mode laser[J].Chin Phys Lett,2003,20:25~27.
[5]Zhou X P,Gao W J,Zhu Shiqun.Fluctuation in a non2 linear laser field wit h couping of additive noise terms[J].Phys Lett A,1996,214:131~138.
[6]Cheng Qing-Hua,Cao Li,Xu Da-Hai,etal.Influence of Noise on Time Evolution of Intensity Correlation Function[J].J Commun Theor Phys,2005,44(5):867~872.
[7] Zhang Li,Cao Li,Wu Dajin.New amplitude equation of single-mode laser[J].Chin Phys,2003,12:33~38.
[8]程庆华,曹力,吴大进.信号调制色泵噪声和实虚部间关联量子噪声驱动下单模激光的随机共振现象[J].Chin Phys Soc,2004,53(8):2556~2561.
[9]张娜敏,徐伟,王朝庆.色噪声驱动的非对称双稳系统的平均首次穿越时间[J].Chin Phys Soc,2007,56(9):5083~5087.
[10]王兵,吴秀清,邵继红.研究了双色噪声驱动非对称双稳系统平均第一穿越时间[J].Chin Phys Soc,2009,58(3):1391~1395.
[11]胡岗.随机力与非线性系统[M].上海:上海科技出版社,1994.

