标准椭圆封头对薄壁内压圆筒承载能力的影响

张红卫， 陈 刚， 刘 岑， 吴元祥， 韩春鸣， 刘小宁*

(1. 武汉软件工程职业学院机械制造工程系，湖北 武汉 430205；2. 武汉工程大学机电工程学院，湖北 武汉 430205)

0 引 言

屈服压力和爆破压力是钢制薄壁内压容器承载能力的基本特征，由于制药和食品等行业常用的不锈钢制薄壁内压圆筒容器，采用的是与圆筒等厚的标准椭圆封头，因此，人们十分关心与圆筒等厚的标准椭圆封头，对不锈钢制薄壁内压圆筒的屈服压力和爆破压力是否有提高作用，如果有，圆筒的长径比应满足什么条件，圆筒的屈服压力和爆破压力怎样计算.为此，文中研究了标准椭圆封头对0Cr13不锈钢制薄壁内压圆筒承载能力的影响.

1 分析

1.1 薄壁内压短圆筒的屈服压力和爆破压力

假设确定不锈钢制薄壁内压短圆筒屈服压力或爆破压力经验公式的形式为

(1)

式(1)中，p1为短圆筒的屈服压力或爆破压力，MPa；a，b为经验系数，由试验数据确定；k为径比，k=1+2δ/Di；δ为壁厚，mm；L为计算长度，包括筒体长度和封头直边高度，mm；Di为内直径，mm；R为圆筒材料的机械性能常数，MPa.

当R分别取圆筒材料的屈服应力Rel与抗拉应力Rm时，p1分别为短圆筒屈服压力p1s与爆破压力p1b.经验系数a，b和相关度r可采用最小二乘法原理回归分析得到.

1.2 薄壁内压长圆筒的屈服压力和爆破压力

薄壁内压长圆筒的屈服压力或爆破压力可用中径公式确定[1]

(2)

式(2)中，p2为薄壁内压长圆筒的屈服压力或爆破压力，MPa.

当R分别取圆筒材料的屈服应力Rel与抗拉应力Rm时，p2分别为短圆筒屈服压力p2s与爆破压力p2b.

1.3 区分薄壁内压长、短圆筒的临界长度

当p1=p2时，由式(1)、(2)可得区分薄壁内压长、短圆筒的临界长度计算公式

(3)

式(2)中，Lcr为区分内压长、短圆筒的临界长度，mm.

LLcr为薄壁内压长圆筒.

1.4 试验容器材料的机械性能

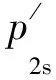
由式(2)可得

(4)

式(4)中，Reli、Rmi分别为第i个长圆筒材料的屈服应力和抗拉应力，MPa；p2si、p2bi分别为第i个长圆筒的屈服压力和爆破压力，MPa；ki为第i个长圆筒的径比.

值得注意的是：(1)p2si、p2bi试验数据是否属于长圆筒要通过式(3)来确定；(2)Reli、Rmi中的最小值不得小于规定值[2].

对于n组试验数据，可得圆筒材料的平均屈服应力Rel和平均抗拉应力Rm.

(5)

2 经验公式

本研究采用0Cr13不锈钢制造的薄壁内压圆筒容器进行常温水压试验.试验容器由单层圆筒及与其等厚的标准椭圆封头组成，内直径Φ400容器，封头直边高度h=25 mm，内直径为Φ600及Φ800容器，封头直边高度h=40 mm.与文献[3]类似，试验容器的爆破口出现在筒体中部附近，呈轴向撕裂，无碎片，是典型的延性爆破[3-4].

采用3个长径比较大的圆筒容器作为内压长圆筒进行试验，研究测得其屈服压力和爆破压力，用式(4)、(5)确定0Cr13钢的屈服应力与抗拉应力，如表1所示.其中Reli均大于规定值205 MPa，Reli均大于规定值440 MPa[2]，表明结果有效.初步将表2中的试验数据作为内压短圆筒的试验数据.

表1 0Cr13不锈钢的屈服应力Rel和抗拉应力Rm

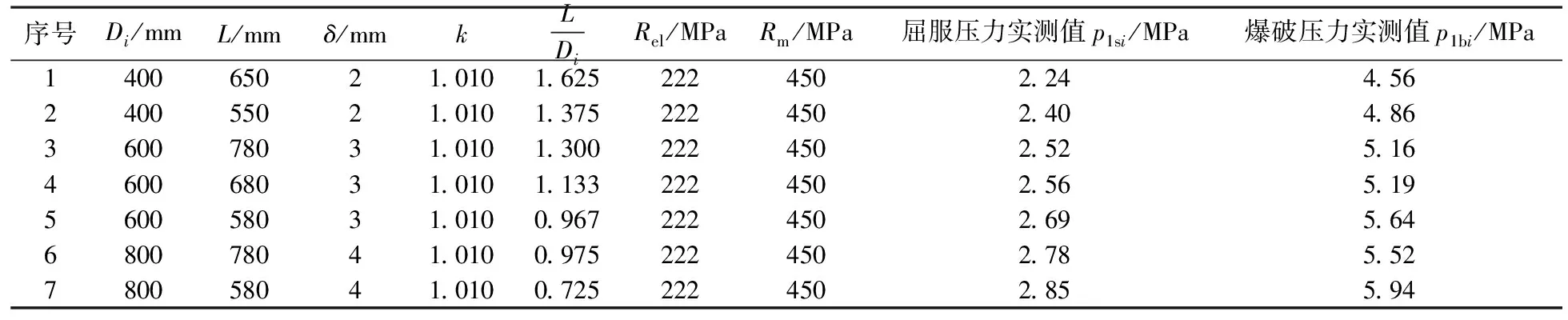
表2 0Cr13不锈钢制薄壁短圆筒屈服压力与爆破压力的试验数据

将表2中7组爆破和7组屈服试验数据，采用最小二乘法原理回归分析，得a=1.228，b=-0.352 4及相关度r=-0.938 2.由式(1)可得不锈钢制薄壁内压短圆筒屈服压力或爆破压力的经验公式

(6)

由式(3)得区分薄壁内压长、短圆筒的临界长度计算公式

Lcr=0.250 5(k+1)2.837 7Di

(7)

当Di=400、600、800，壁厚对应为δ=2、3、4时，k=1.010，由式(7)得Lcr/Di=1.817，因此，表1中的数据为长圆筒屈服压力和爆破压力试验数据，用其确定试验材料的屈服应力和抗拉应力是可行的；同时可知，表2中的试验数据也均为短圆筒屈服压力和爆破压力试验数据.

3 验 证

文献[3]基于水压试验，得到4组0Cr18Ni9Ti不锈钢制薄壁内压圆筒(标准椭圆形封头) 屈服压力和爆破压力试验研究数据，如表3所示.

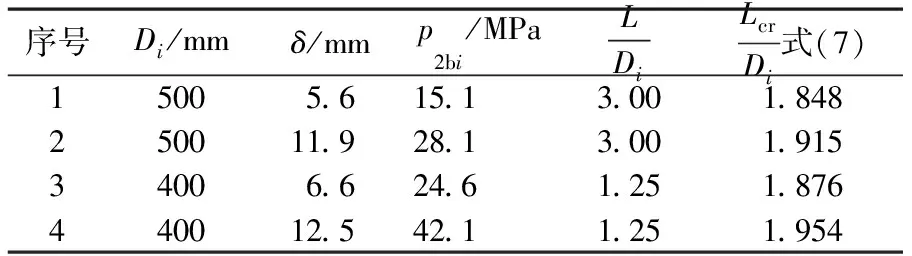
表3 0Cr18Ni9Ti不锈钢制薄壁圆筒爆破压力试验数据

由表3可知：1～2号圆筒是薄壁内压长圆筒，3～4号圆筒是内压短圆筒.可用1～2号圆筒试验数据和式(5)确定0Cr18Ni9Ti钢的抗拉应力，如表4所示.其中Reli大于规定值520 MPa[2]，表明结果有效.

表4 0Cr18Ni9Ti不锈钢的抗拉应力Rm

表3中3～4号薄壁内压短圆筒的试验数据验证结果如表5所示.

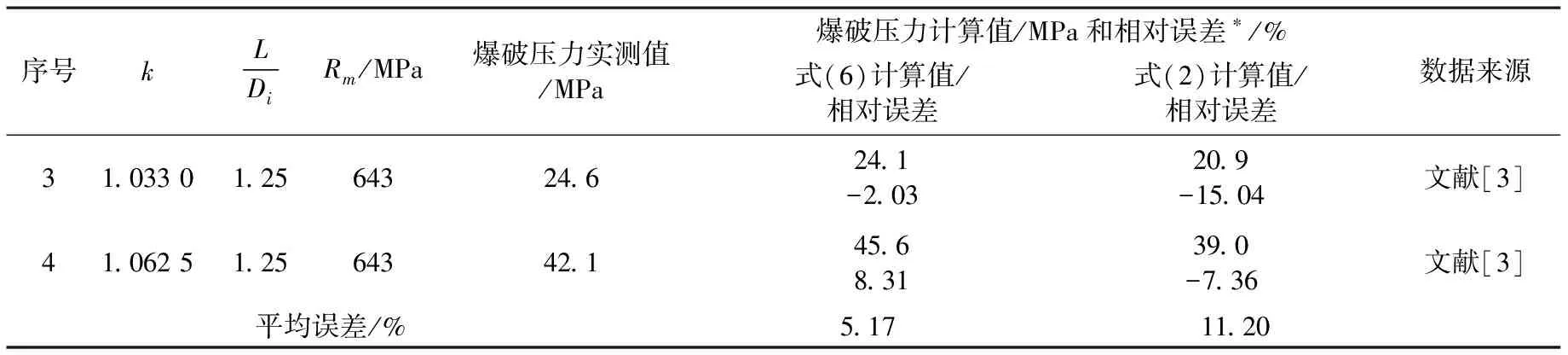
表5 0Cr18Ni9Ti不锈钢制薄壁短圆筒爆破压力的实测值与计算值

*相对误差=(计算值—实测值)/实测值×100%.

由表5可知，用中径公式(2)计算0Cr18Ni9Ti钢制薄壁内压短圆筒爆破压力，计算值偏小，相对误差较大；用经验公式(6)计算0Cr18Ni9Ti钢制薄壁内压短圆筒爆破压力，相对误差较小.

4 讨 论

4.1 不锈钢制薄壁内压长、短圆筒的最小临界长度

不锈钢制薄壁内压圆筒形容器的最小壁厚δmin=0.002Di[1]，即最小径比k=1.004，如果容器采用的标准椭圆形封头与圆筒等厚，则其最小临界长度由式(7)可得Lcr=1.801Di，故计算长度L≤1.801Di的0Cr13和0Cr18Ni9Ti不锈钢制薄壁内压圆筒是内压短圆筒.

4.2 不锈钢制薄壁内压长、短圆筒承载能力的比较

由式(6)与式(2)得

因最小径比k=1.004，故有

常用的不锈钢制薄壁内压短圆筒容器的L/Di=1.801～0.5，有p1/p2>1.00～1.57，表明随着长径比的变小，与圆筒等厚的标准椭圆封头，对不锈钢制薄壁内压短圆筒屈服压力或爆破压力的提高作用越来越显著，即短圆筒的承载能力比长圆筒的大.

4.3 不锈钢与低碳钢制薄壁内压短圆筒的比较

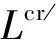
(8)

L’cr=0.244 3(k+1)2.750 3Di

(9)

由式(6)、(8)得

p1/p’1=1.025(L/Di)0.011 2

对常用的L/Di=0.5～1.801不锈钢制薄壁内压短圆筒容器，有p1/p’1=1.017～1.032，表明用式(6)计算不锈钢制薄壁内压短圆筒的屈服压力或爆破压力，与用式(8)计算低碳钢制薄壁内压短圆筒的无显著差异.

由式(7)、(9)得

Lcr/L’cr=1.025(k+1)0.087 4

由于不锈钢制薄壁内压短圆筒的最小径比k=1.004，故Lcr>1.089L’cr，表明不锈钢制薄壁内压短圆筒的承载能力，对受到有足够强度和刚度的封头加强作用比较敏感.

4.4 单层厚壁内压圆筒的临界长径比

当单层厚壁内压圆筒的径比分别为2与2.5时，由式(7)可得其临界长径比分别为5.66与8.76，表明“当单层厚壁内压圆筒的径比为2或2.5，长径比为4时，封头对爆破压力的增强作用才可以忽略”[5]的看法有一定的试验基础.

5 结 语

(1)与圆筒等厚的标准椭圆封头，可提高不锈钢制薄壁内压短圆筒的承载能力.基于试验研究，得到确定0Cr13不锈钢制薄壁内压短圆筒屈服压力和爆破压力的经验公式，以及区分薄壁内压长、短圆筒的临界长度计算公式.采用0Cr18Ni9Ti不锈钢制薄壁内压圆筒的爆破压力试验数据，验证了文中方法的有效性和合理性.

(2)当0Cr13和0Cr18Ni9Ti不锈钢制薄壁内压圆筒采用与圆筒等厚的标准椭圆封头时，在长径比不大于1.801时是内压短圆筒，随着长径比的变小，标准椭圆封头对不锈钢制薄壁内压短圆筒承载能力的提高作用越来越明显.

(3)与低碳钢制薄壁内压短圆筒相比，0Cr13和0Cr18Ni9Ti不锈钢制薄壁内压短圆筒的屈服压力和爆破压力，对受到与圆筒等厚的标准椭圆封头的加强作用比较敏感.

参考文献：

[1]丁伯民,黄正林.化工容器[M].北京:化学工业出版社,2003:54-57.

[2]王非,林英.化工容器用钢[M].北京:化学工业出版社,2004:369.

[3]马 利,郑津洋,寿比南,等.奥氏体不锈钢制压力容器强度裕度研究[J].压力容器,2008,25(1):1-5.

[4]刘小宁,张红卫,刘 岑,等.钢制薄壁内压短圆筒静强度的试验研究[J].压力容器,2009,26(7):11-14.

[5]邵国华,魏兆灿.超高压容器[M].北京:化学工业出版社,2002:21.