关于资本限额影响投资决策的思考
张 彬
一、企业投资决策概述
在考虑货币时间价值的情况下,企业做出投资决策所采用的方法有:净现值法(NPV法)、内含报酬率法(IRR法)、获利能力指数法(PVI法)等。如何在有限的资金范围内做出投资决策为企业获取更大的投资价值是下文研究的主要内容。
二、资本限额下投资决策的举例
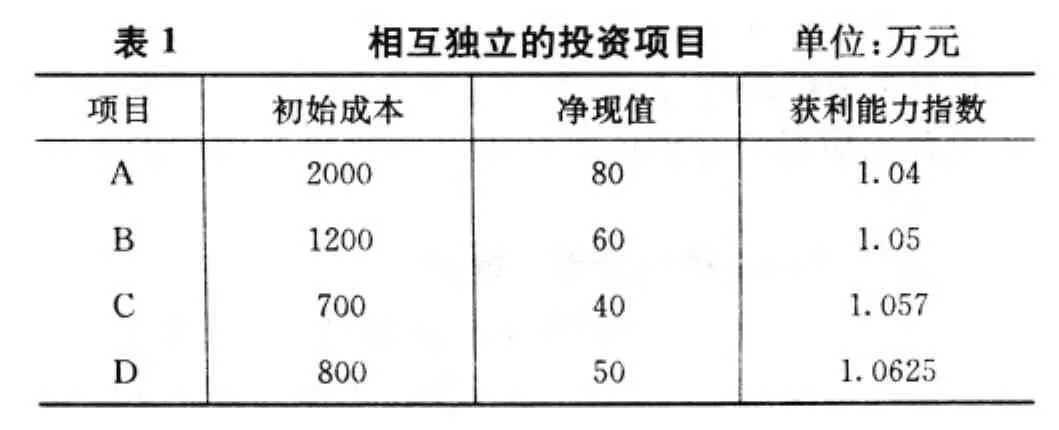
某企业用于投资的预算资本即资本限额是2000万元,面对四个相互独立的投资项目A、B、C、D(见表1),企业该做出怎样的投资决策选择。
?
显然,按照通常投资决策的办法,四个项目净现值都大于零,获利能力指数都大于1,因此都具有投资的可行性。然而由于资金所限,企业无法全部投资于所有的项目,这就需要评价哪个(或哪组)项目能使企业投资价值最大化。从表1中可以看出,A项目得到的净现值最大,但是企业若将有限的资本金全部投入到A项目,那么得到的净现值就只有80万元,企业没有资金再投入到其他项目,因此,单投资于A项目显然是不合适的,应以组合项目作为投资选择。对于B、C、D三个投资项目,经分析在资本限额下获得的最大净现值的组合应为投资于项目C和D以及项目B的5/12,得到的净现值为115万元(40+50+5/1260),而其它他投资项目组合得到的净现值均小于这一值。对于投资项目无法分割或分割后得到的净现值减少的比例高于分割比例,投资决策又会怎样安排呢?投资项目不可细分且在资本限额约束下,投资于B、D项目得到的净现值最大,为110万元。
三、资本限额下做出投资决策的方法
1.面对众多的投资方案,从价值最大化的角度来说,企业只有将资金投资于净现值最大的项目才可以获得比其他投资对象更好的投资回报。对于相互独立可以分解的若干投资项目,可以采用前文的投资分析做出决策。在分析可以分解的投资项目时,我们并不是以单个独立项目所获得的净现值这一指标来判断投资的可行性,而应以获利能力指数作为资本限额下判断可分解项目可行与否的指标。获利能力指数反映了现金流入现值与现金流出现值的比例,是一个相对数指标。该指标衡量了资金投入与产出的关系,也就是体现了每一单位的资金投入可以获得多少单位的投资回报。在一定的资本限额下,投资者关注的是每一单位投资所获得的效益,高获利能力指数的备选项目就应作为首选,其次是较低的项目。如前例,D项目的获利能力指数最高,C项目次之,B项目再次之。因此,按照获利能力指数高低顺序安排的投资组合最终得到的净现值是最大的。
2.对相互独立的不可分解的投资项目做出决策,掌握的原则应为选取在资本限额下,取得最大净现值的项目组合。备选的投资项目可能具有较高的净现值,例如单独投资前例中的A项目,虽然可以获得最大的净现值,但相对于其他的投资组合而言,得到的净现值并非最大即未实现价值最大化。面对不可以分解的投资项目,选择的方法是计算在资本限额下,不超过资本预算所有可能的投资项目组合的净现值之和,比较净现值和最大的组合作为投资对象。
3.在投资实务中,企业面临的可投资项目数量众多,可供选择的投资组合也多。因此,试算所有投资组合的净现值会过于繁琐。在众多的备选投资项目中选择净现值总和最大的投资项目(或组合)可以采用线性规划的方法。该线性规划的数学模型是:

设X为自变量,每一个投资项目的净现值为npvi,线性规划的目标函数为投资组合净现值总和最大即MaxNpv,目标函数可以通过各个项目净现值与自变量的乘积之和表示;约束条件是:X应为整数,X的取值只能是0或1。等于1,表示采用,等于0,表示放弃;投资组合的初始投资额要小于等于资本限额F。该模型的求解可以采用Excel中规划求解工具,最终得到的结论如果Xi=1,表示方案的选择,Xi=0表示方案的放弃。所有Xi=1的方案构成了在资本限额下的投资组合。

