一种面向隐含主题的上下文树核

徐 超 周一民 沈 磊

(北京航空航天大学计算机学院 北京 100191)

1 引言

核方法是模式识别中一种有效的方法，它通过核函数将低维空间线性不可分问题映射到高维空间，变成线性可分问题。核方法在分类、聚类和回归分析等领域具有广泛的应用。尤其是在结构化数据(文本、图像等)学习上的优势，使其在文本挖掘中受到越来越多的关注[1]。核方法的一个基本问题是核函数的设计。近年来，人们针对不同的文本表示方式，提出了很多文本核函数的构造方法。这些方法基本上可分为三类：一类是以向量空间模型作为文本表示，用线性核函数计算向量空间核，这种方法计算简单，但是没有考虑词与词之间的语义关系。为了解决这个问题，泛化的向量空间核采用词的相似度作为计算核的加权。文献[2]则利用潜在语义索引作为权值，构造了潜在语义核。但是这类方法无法表达文本的结构信息。另一类把文本表示成结构化对象，通过定义在子结构上的卷积构造核函数，被称为卷积核，主要有字符串核、词串核、树核和图核等。卷积核可以充分考虑文本内部各个语法成分之间的关系，但是卷积运算的计算量很大，因此在实际应用中受到限制。第三类方法以文本的概率生成模型进行核嵌入，称为生成模型核，主要有Fisher核[3]、概率文本核[4]等。这类方法在贝叶斯框架下进行推理，具有很好的概率基础，但是目前的方法都是基于词频统计，缺乏词语的语义信息。核函数可以看成是两个样本间的一种相似性度量，上述三类方法都是在文本表示的基础上，通过定义相似性来进行核函数构造。充分利用文本的结构和语义信息，采用合理的文本间相似性度量方法是当前文本核函数研究的出发点。

Cuturi等人[5]以信息论为基础，采用互信息核的思想构造了一种用于序列数据的上下文树核(context tree kernel)。上下文树核以上下文树模型作为序列的基本生成模型，利用概率模型间的互信息计算核函数的值。与序列分析中的串核[6]相比，上下文树核采用上下文树加权算法降低了计算量，而且模型不需要调节过多的外部参数。文献[5]将上下文树核应用于蛋白质序列的分类中，取得了很好的效果。但是将上下文树核直接用于文本分类时会遇到一些困难。由于文本中的字符不是语义的基本单位，因此以字符为单位的上下文树核难以表达文本的主题。而文本中大部分词语出现的频率较低，直接将词作为模型的基本单位时会带来统计数据的稀疏性[7]。为此，本文在文献[5]工作的基础上，提出了一种面向隐含主题的上下文树核。该方法以词语所表达的隐含主题为单位构造上下文树模型，解决了上下文树核缺乏语义信息和词语统计稀疏性的问题，能够更合理地表示文本的内容。在测试集上的文本聚类实验表明，该方法能够获得较好的效果。

2 上下文树核

上下文树加权(CTW)算法是一种通用信源编码算法，最先被应用于文本压缩领域[8]。该算法使用上下文树模型对所有有界记忆树形信源加权统计，从而获得一个可变阶 Markov链的信源概率分布。随机文本序列的建模中同样需要得到数据源的随机特征，因此上下文树模型也被应用于语言建模中，并且解决了文本分类[7]和聚类问题[9]。

上下文树模型采用后缀树的形式表示串序列，如图1所示。图中上下文树的根结点代表下一个将要出现的字符。由叶节点到根节点的路径上的字符串代表下一个出现的字符的上下文，也就是当前字符串的一个后缀。叶节点上的权值代表文本中该字符串作为后缀，后面生成每个字符的概率θ，这里θ维数为文本中出现的全部字符数。因此，上下文树也被称为概率后缀树。所有的叶节点所表示的字符串的集合被称成为当前上下文树的完全后缀字典。一旦给定了一棵上下文树，就可以确定一个完全后缀字典。对于一个文本，在上下文树模型上所对应的所有概率构成了文本的生成模型。

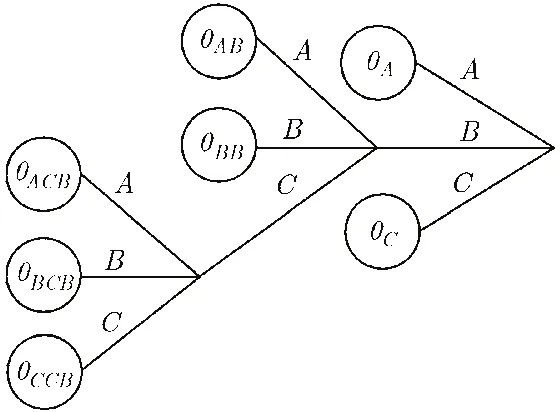
图1 上下文树模型

在生成模型方法中，一个数据样本被看作是由模型和模型上的参数以一定的概率生成的，模型空间和每个模型上的参数空间构成了数据的一个生成源模型。因此，知道了数据样本在模型空间和参数空间的分布也就知道了数据的来源。每个模型上数据的生成概率代表了数据对此模型的拟合程度，从而可以判断出任何两个数据来自同一个模型的可能性。可以用一个分布族来定义一个生成模型，其中F是模型空间，Θf是模型f的参数空间，参数θf是Rn的子集，其中n被称为模型的维数。Pf,θf是数据在参数为θf的模型f上的概率。这里定义为数据X在分布族上所有可能的概率。如果用每个分布来表示一个类，则φ(X)表示数据X符合每个类的程度。

对于两个概率分布，一般采用互信息来衡量概率分布的相似程度。因此，对于数据X和Y，可以构造如下的互信息核[6]：

其中βi是给定的Dirichlet分布参数，d是文本中出现的不同字符数。

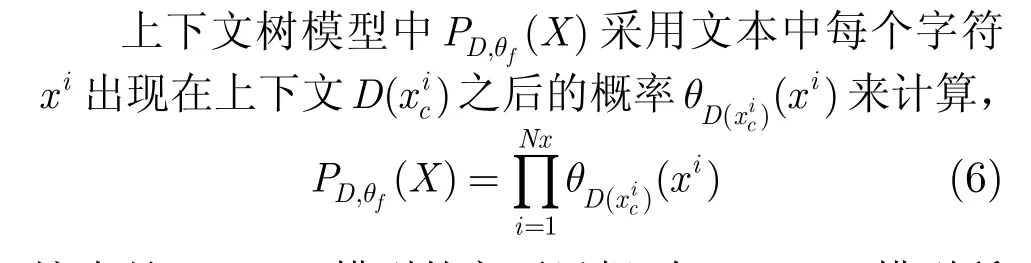
这也是Markov模型的主要思想。与Markov模型所不同的是，上下文树模型可以表示可变长度的上下文，而不像Markov模型必须指定模型的阶数。

由式(2)-式(6)，可以得到上下文树核的计算公式为[6]

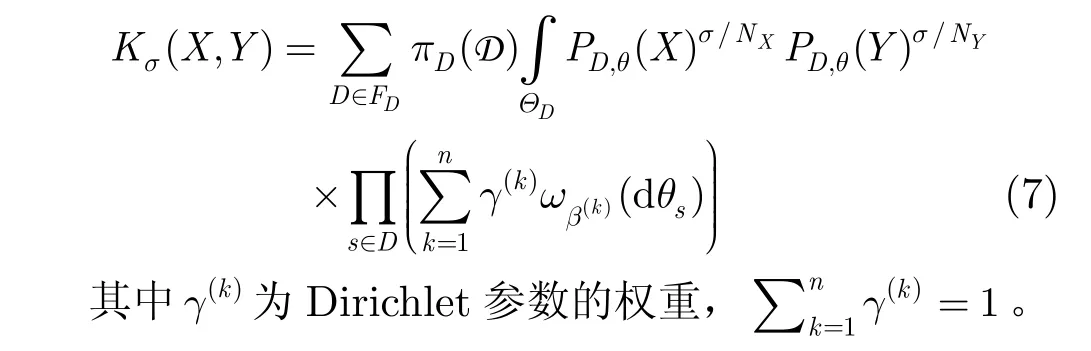
从上面的分析可以看出，文本上下文树核的计算包括3部分内容：(1)以上下文树模型构造文本表示模型；(2)估计文本模型中参数的后验概率；(3)以互信息方法计算两个文本模型的核函数。

3 面向隐含主题的上下文树核

3.1 上下文树模型的建立

建立上下文树模型是计算上下文树核的关键一步。上下文树模型的结点反映了所研究对象的基本结构。在文献[7,9]中，将文本看作是由字符所组成的序列，采用文本中出现的字符作为上下文树的节点，建立文本的上下文树模型。尽管该方法对于解决文本的类型聚类问题效果较好，但由于文本中的字符没有实际的语义含义，这种建模方法将丢失文本的语义信息，特别是不能解决语言中普遍存在的同义词和多义词现象。词语是语言中最小的语义单元，因此就文本模型而言，词是比字符更合理的文本表示单位。但是将词直接用于上下文树模型的构造中会带来两方面的问题。一方面，文本中的词汇数量很多，远远大于字符的数量。上下文树核递归算法的计算复杂性与树的分支数有关，树节点的增加严重影响了计算的效率。另一方面，由于大部分词在文本中出现的频率很低，从而造成了统计数据的稀疏性，这也是文献[7]中没有将词作为基本单位的原因。为了解决数据稀疏的问题，在统计语言模型中采用了词聚类的方法，用词类来代替词作为统计的单位[10]。这里将词聚类的思想用于上下文树模型的构建中。由于词类的数量小于文本中词语的数量，而且词聚类对语义相似的词语进行归并，从一定程度上消除了同义词的问题。因此，将词类作为建立上下文树的基本单位，能够解决直接采用词作为结点时所遇到的问题。

3.2 面向隐含主题的特征集合构建

目前词聚类的研究主要有两个思路，即采用层次分类的方法和基于统计模型的方法。层次分类的方法需要外部语义词典的辅助，应用上受到很多限制。目前基于统计模型的方法主要采用概率隐含语义分析(PLSA)[11]，这种方法的参数空间和训练数据的个数成正比，不利于对大规模文本的处理。隐含狄利克雷分配(LDA)[12]是文本建模的一种生成模型方法，该模型将主题混合权重视为潜在随机变量，而不是与训练数据直接联系的个体参数集合，克服了PLSA方法的不足。这里采用LDA模型，给出了一种新的词语主题聚类的方法。

LDA方法的基本思想是文档被表示为一些隐含主题的随机混合，其中每个主题由单词的分布确定。LDA模型认为文档通过下面的过程生成[12]：

其中m满足这种映射方法避免了一般词聚类方法所需的聚类操作，不但减少了计算时间，而且消除了聚类算法性能差异对结果的影响。

通过定义词语到隐含主题的映射，可以构造面向隐含主题的上下文树核为

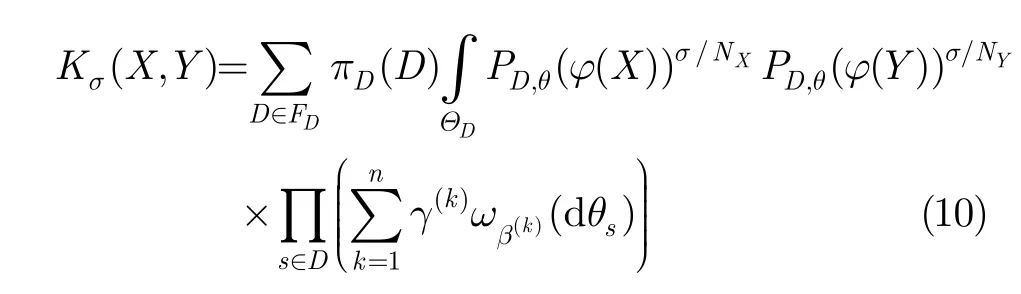
这里Kσ(X,Y)可以采用文献[5]中的方法进行计算，其中将X和Y中所有出现的词x和y分别用相应的隐含主题ϕ(x)和ϕ(y)代替。

通过上述的分析，可以给出面向隐含主题的上下文树核的构造算法如下：

(1)对文本集合进行预处理，得到文档-词矩阵。

(2)计算词对应隐含主题的概率：

(a)建立文档-词矩阵的LDA模型，通过Gibbs采样或变分Bayes方法得到文本中词与隐含主题的概率关系矩阵，矩阵中的每一项即为每个词语对应隐含主题的概率。

(b)根据词与隐含主题的概率关系，选择每个词所对应的概率最大的一个作为该词所对应的隐含主题，从而得到词空间到隐含主题空间的映射。

(3)将文本看作由词所构成的序列，根据式(10)计算任意两个文本的上下文树核，得到核矩阵。

由算法得到的文本核可以用于各种基于核的模式分析方法中，如支持向量机和谱聚类等方法，从而能够解决文本分类和聚类等问题。

4 实验结果及分析

4.1 实验设计和评价标准

为了验证文中所提出的方法的有效性，在Reuters21578数据集上进行文本聚类的实验。Reuters21578数据集的特点是各类样本的个数差别很大，具有很强的不平衡性。而且，各类样本主题之间的相关性不同，这种类之间的相关性决定了将各类分开的难易程度。文献[13]对 Reuters21578数据集的相关性进行了研究，分别给出了其中相关性最大和最小的5对数据集。本文在ModApte划分方法的测试文本集上对文献[13]中所给出的10对数据集进行聚类实验。

对于文本集中的文本首先除去与主题无关的时间等信息，同时去掉不包含实际内容的文档，最后去停止词。不对词语做 stemming处理，而是保留词形变化的信息。采用本文中所给出的方法计算得到核矩阵后，采用核聚类算法对文本集进行聚类。这里所采用的核聚类算法是通常采用的谱聚类算法。

同分类结果不同，聚类结果只给出样本簇的划分，而不能给出簇所属的类别。为了确定聚类簇所对应的类别，需要从每个聚类簇中挑选最优的指标值，以该指标值对应的类别作为聚类簇的类别，并以此来判定的聚类质量。F值和熵是常用的两种聚类效果评价指标[14]。F值是准确率和召回率的综合，F值越大表示划分的聚类簇与文本集合的类别越相似。熵是簇中样本散乱程度的度量。如果熵值很大，说明该簇的样本分散到各个类别中，聚类的效果很差。反之，熵值越小，说明聚类的效果越好。

4.2 结果分析

本文分别采用上述两个度量指标，评价了文中方法的聚类效果。并且分别与向量空间模型、字符串核以及文献[5]中基于字符的上下文树核方法的聚类结果进行比较。向量空间模型是目前文本表示中最常用的方法，而字符串核方法是一种效果较好的文本分类方法。表1分别列出了训练集中相关性最大和最小的5对样本集的聚类结果。

从表中可以看出，在相关性最大也就是最难区分的5对数据集中，4种聚类方法的性能差别不大，基于主题的上下文树核方法在其中4个数据集上高于其它方法。在相关性最小的5对数据集中，基于主题的上下文树核方法在其中4个数据集上性能明显高于其它的方法。

隐含主题个数是算法中需要预先的指定参数，实验中对主题数分别取为 20-140之间的性能进行评价，其结果如图2所示。

从图2中可以看出，F值在主题数40-80之间基本上是性能最优的区间。同样，熵也在主题数40-80之间较小。从图中也可以看出，F值在20处一般也较大，但此时的熵也比较大，这主要是由于在主题数很小时，主题的划分过粗，使得大部分文章都被划分到一个类别中，产生了类偏斜的现象。因此，应选择文本主题数目在40-80之间。另外还可以看出在不同的数据集合中，最佳的主题数目并不相同。如何确定一个文本集合的最佳主题数 LDA方法有待解决的问题。除了采用通常的交叉验证方法外，自动的主题数目确定是今后的一个研究方向。

5 结论

本文提出了一种用于文本挖掘的上下文树核。首先采用隐含狄利克雷分配将文本中的词语映射到隐含主题，然后以隐含主题为单位建立上下文树模型，最后利用模型间的互信息构造上下文树核。这种面向隐含主题的上下文树核解决了基于字符的上下文树核缺乏语义信息的问题，能够合理表达的文本之间的主题相似性。在Reuters21578数据集上的文本聚类实验表明，本文的方法同其它方法相比具有更好的性能。

表1 Reuters21578 Test数据集聚类结果

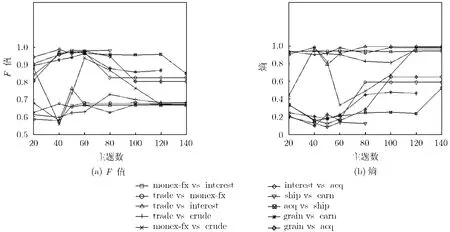
图2 隐含主题数对聚类性能的影响

[1] Srivastava A N and Sahami M. Text Mining: Classification,Clustering, and Applications[M]. Boca Raton: Chapman and Hall, 2009: 1-25.

[2] Cristianini N, Shawe-Taylor J, and Lodhi H. Latent semantic kernels[J].Journal of Intelligent Information Systems, 2002,18(2/3): 127-152.

[3] Nyffenegger M, Chappelier J C, and Gaussier É. Revisiting Fisher kernels for document similarities[C]. 17th European Conference on Machine Learning, Berlin, Germany,September 18-22, 2006: 727-734.

[4] Lehmann A and Shawe-Taylor J. A probabilistic model for text kernels[C]. Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, 2006:537-544.

[5] Cuturi M and Vert J P. The context-tree kernel for strings[J].Neural Networks, 2005, 18(8): 1111-1123.

[6] Yin Chuan-huan, Tian Sheng-feng, and Mu Shao-min,et al..Efficient computations of gapped string kernels based on suffix kernel[J].Neurocomputing, 2008, 71(4-6): 944-962.

[7] Vert J P. Text categorization using adaptive context trees[C].Proceedings of the Second International Conference on Computational Linguistics and Intelligent Text Processing,Mexico City, Mexico, February 18-24, 2001: 423-436.

[8] Willems F M J, Shtarkov Y M, and Tjalkens T J. The context-tree weighting method: basic properties[J].IEEE Transactions on Information Theory, 1995, 41(3): 653-664.

[9] Vert J P. Adaptive context trees and text clustering[J].IEEE Transactions on Information Theory, 2001, 47(5): 1884-1901.

[10] 李晓光, 于戈, 王大玲等. 基于信息论的潜在概念获取与文本聚类[J]. 软件学报, 2008, 19(9): 2276-2284.Li Xiao-guang, Yu Ge, and Wang Da-ling,et al.. Latent concept extraction and text clustering based on information theory[J].Journal of Software, 2008, 19(9): 2276-2284.

[11] Hofmann T. Probabilistic Latent Semantic Analysis[C].Proceedings of the 15th Conference on Uncertainty in Artificial Intelligence, Stockholm, Sweden, July 30-August 1,1999: 289-296.

[12] Phan Xuan-hieu, Nguyen Le-minh, and Horiguchi Susumu.Learning to classify short and sparse text & web with hidden topics from large-scale data collections[C]. Proceeding of the 17th International Conference on World Wide Web, Beijing,China, April 21-25, 2008: 91-100.

[13] Pinto D and Rosso P. On the relative hardness of clustering corpora[C]. Proceedings of 10th International Conference on Text, Speech and Dialogue, Pilsen, Czech Republic,September 3-7, 2007: 155-161.

[14] 周昭涛. 文本聚类分析效果评价及文本表示研究[D]. [硕士论文], 中国科学院计算技术研究所, 2005.Zhou Zhao-tao. Quality evaluation of text clustering results and investigation on text representation[D]. [MA.dissertation], Institute of Computing Technology, Chinese Academy of Sciences, 2005.