基于高斯粒子JPDA滤波的多目标跟踪算法

张俊根 姬红兵 蔡绍晓

(西安电子科技大学电子工程学院 西安 710071)

1 引言

多目标跟踪系统通过运用随机统计决策、自适应滤波、知识工程和信息融合等现代技术，将各传感器接收到的信号数据分解为对应于各种不确定运动信息源所产生的不同观测集合或轨迹，一旦轨迹被确认，则可相应地估计出各目标的状态，所涉及的问题是控制、指挥、通信、计算机、情报、监视和侦察科学发展的前沿问题，是当前国际上的热门研究方向[1]。

多目标跟踪方法中，基于贝叶斯框架的联合概率数据关联滤波器(JPDAF)是比较理想的方法，对于各目标的有效观测，JPDAF列举所有可能的目标与观测的关联假设，并计算关联概率，利用联合关联新息更新目标状态。根据实际问题人们不断提出一些改进方法，如联合综合概率数据关联滤波算法(JIPDAF)[2]，广义概率数据关联滤波算法(GPDAF)[3]。对于非线性非高斯系统模型，文献[4-6]将 JPDAF与粒子滤波(PF)相结合，提出了基于蒙特卡罗JPDAF(MC-JPDAF)的多目标跟踪方法，将数据关联问题直接在粒子滤波思想下进行解决；文献[7,8]提出了马尔科夫链蒙特卡罗数据关联算法(MCMCDA)，利用MCMC技术近似计算JPDA，然而，MCMC方法需要进行迭代运算，收敛所需的迭代次数不确定，不适合在线应用。

本文在 JPDA的框架下，结合高斯粒子滤波(GPF)[9]的思想，提出一种新的基于高斯粒子JPDAF的多目标跟踪算法，通过高斯粒子来近似目标与观测的边缘关联概率，利用GPF对目标状态进行预测及更新，将它应用于被动多传感器多目标跟踪，仿真结果表明所提算法的跟踪性能要优于MC-JPDAF。

2 系统模型及贝叶斯序贯估计

3 多目标滤波

对于非线性目标跟踪问题，已经证明，在高斯假设下，GPF估计的状态变量能依概率1渐近收敛于最小均方值，相比于其它高斯滤波算法，如EKF及其改进算法，GPF具有更好的性能，特别是当存在较强非线性的时候。另一方面，不像 PF估计时要进行重采样，GPF不需要重采样，避免了一些应用中发生的偏差积累现象，并且，提供了并行处理的可能。本文结合GPF和JPDAF的思想，利用高斯粒子来替代标准 JPDAF中的高斯量，计算目标与观测的边缘关联概率及目标状态的滤波分布，可以改善目标跟踪性能[9,10]。

3.1 高斯粒子JPDAF(GP-JPDAF)算法

3.2 目标跟踪门

多目标跟踪中，在计算目标与观测的联合关联概率时，为减少关联假设的数量，需要对观测进行有效性判别，以映射到观测空间的目标状态值为中心，建立一个跟踪门，对落入此门限内的观测值才被考虑为具体目标关联的可能的候选观测。

3.3 GP-JPDAF算法小结

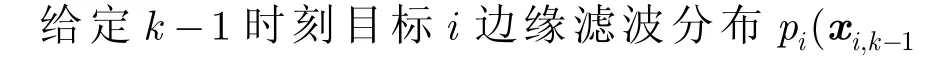
4 仿真结果与分析

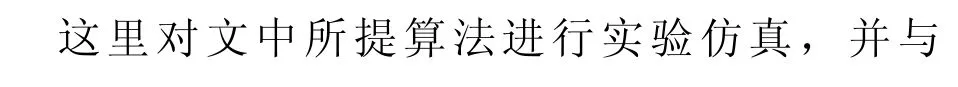
图1为传感器位置与目标运动轨迹，Δ表示传感器位置，o表示目标运动起始位置，图2-图4分别给出了3种不同条件下两种算法随粒子数变化的RMSE统计结果，对应于粒子数的·表示均值，竖线表示标准差。可以看出，在各目标的整个跟踪过程中，对于一定的粒子数，本文提出的GP-JPDAF算法的目标跟踪精度比 MC-JPDAF要高，并且GP-JPDAF估计目标位置比MC-JPDAF算法要可靠；随着算法采用粒子数的增多，两种算法跟踪精度都有所提高，当粒子数大于200时，GP-JPDAF相比于 MC-JPDAF的改善性能会减小，当粒子数增至1000时，两种算法的目标跟踪性能相当；随着观测条件的变坏，检测概率变小、杂波密度变大，即，从条件A到条件C，目标与观测关联的难度将增大，两种滤波算法的目标跟踪误差略有增大。需要指出的是，这两个滤波器对于目标位置的估计，仅仅是从平均意义下考虑的，更重要的是，估计的方差决定了滤波器的有效性，因为对于任何一次给定的样本路径，GP-JPDAF算法估计的结果比MCJPDAF要准确可靠。

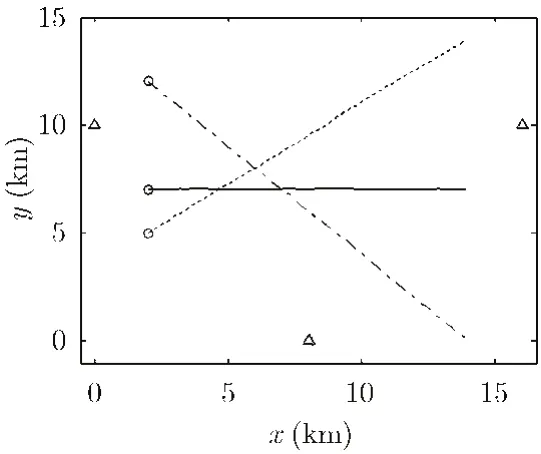
图1 传感器位置及目标运动轨迹

图5给出了不同观测条件下各算法的失跟率对比，可以看出，在观测条件一定、粒子数一定的情况下，GP-JPDAF算法的目标失跟率比MC-JPDAF要低；随着粒子数的增多，两种算法的目标失跟率都将减小；这两种算法随着观测条件难度的增大，失跟率会有所增大。

图 6给出了不同观测条件下平均运算时间对比，可以看出，随着粒子数的增多，两个滤波器的运算量呈指数增长，给定粒子数，MC-JPDAF算法由于增加了重采样计算，运算时间比GP-JPDAF要大；随着观测条件难度的增大，两种滤波算法的耗时也略有增加；由于GP-JPDAF算法不需要进行粒子重采样，利用GPF的可并行处理性质，能使算法的运行时间大大降低。

5 结束语

本文提出了一种新的基于高斯粒子 JPDAF的多目标跟踪算法，该算法通过高斯粒子来近似目标与观测的边缘关联概率，利用GPF的渐进最优性实现对目标状态的预测及更新，将其应用到被动多传感器多目标跟踪中，仿真结果表明，本文提出的GP-JPDAF算法的跟踪性能要优于MC-JPDAF算法，算法运算时间比 MC-JPDAF也要小，但是适用范围比MC-JPDAF要小，因为MC-JPDAF算法可以应用于非高斯情况。

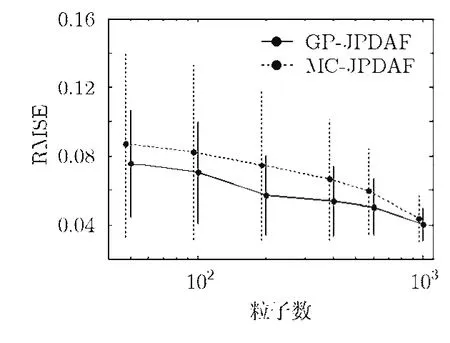
图2 100次实验RMSE的统计结果(条件A)

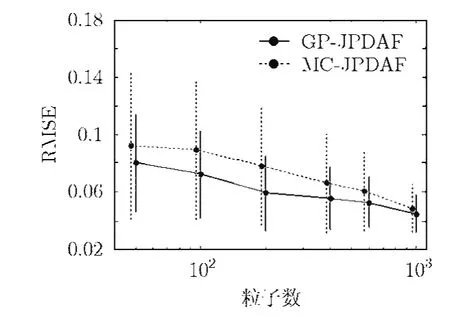
图3 100次实验RMSE的统计结果(条件B)

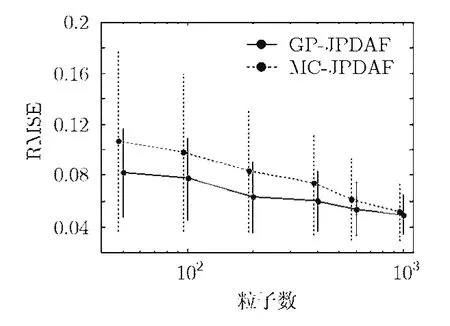
图4 100次实验RMSE的统计结果(条件C)

图5 不同观测条件下算法失跟率对比

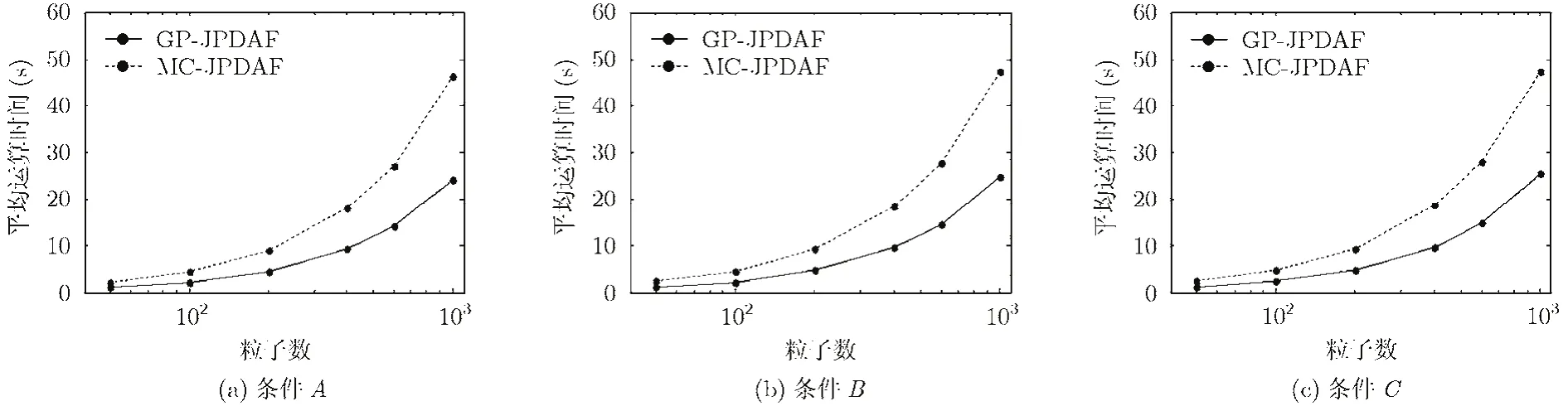
图6 不同观测条件下算法平均运算时间对比

[1] Bar-Shalom Y and Li X R. Multitarget-Multisensor Tracking:Principles and Techniques[M].Storrs: YBS Publishing, 1995.

[2] Musicki D and Suvorova S . Tracking in clutter using IMMIPDA-based algorithms[J].IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 111-126.

[3] 潘泉, 叶西宁, 张洪才. 广义概率数据关联算法[J]. 电子学报,2005, 33(3): 467-472.

[4] Karlsson R and Gustafsson F. Monte Carlo data association for multiple target tracking[C]. Proceedings of the IEE Seminar on Target Tracking: Algorithms and Applications,Enschede, Netherlands, 2001: 13/1-13/5.

[5] Vermaak J, Godsill S J, and Perez P. Monte Carlo filtering for multi-target tracking and data association[J].IEEE Transactions on Aerospace and Electronic Systems, 2005,41(1): 309-332.

[6] Ekman M. Particle filters and data association for multi-target tracking[C]. 2008 11th International Conference on Information Fusion, Cologne, Germany, July 2008: 1-8.

[7] Pasula H, Russell S J, Ostland M, and Ritov Y. Tracking many objects with many sensors[C]. Proc. Int. Joint Conf.Artif. Intell., Stock-holm, Sweden, 1999: 1160-1171.

[8] Oh S, Russell S, and Sastry S. Markov chain Monte Carlo data association for multi-target tracking[J].IEEE Transactions on Automatic Control, 2009, 54(3): 481-497.

[9] Kotecha J H and Djuric P M . Gaussian particle filtering[J].IEEE Transactions on Signal Processing, 2003, 51(10):2592-2601.

[10] Zhang Zhi-qiang, Wu Jian-kang, and Huang Zhi-pei.Wearable sensors for realtime accurate hip angle estimation[C]. 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 2008: 2932-2937.

[11] Cappe O, Godsill S J, and Moulines E. An overview of existing methods and recent advances in sequential Monte Carlo[J].Proceedings of the IEEE, 2007, 95(5): 899-924.