基于Logistic映射的图像加密安全风险研究
章秀君 ,冯乔生 ,罗 可 ,方 正
(1.云南师范大学 计算机科学与信息技术学院,云南 昆明 650092;2.中国地质大学 工程学院,湖北 武汉 430074)
混沌理论的发展为图像加密提供了新思路。混沌是确定性系统,但由其产生的序列是伪随机的、不可预测的、在理想条件下具有无限大的周期,可以提供巨大的密钥空间、是非周期又不收敛的。更重要的是,混沌系统对初值变化极端敏感,即初始状态只有微小差别的两个同构混沌系统在短时间就会产生两组完全不同的、互不相关的混沌序列值。由于安全性高、加密速度快,基于混沌的图像加密技术得到了广泛的研究[1-9]。
目前按照变换方式的不同,基于混沌的图像加密可分为图像像素坐标变换和图像像素值变换加密方式两大类。其中,图像像素坐标变换的加密方式也称置乱方法,是通过一些混沌映射改变像素的坐标位置,从而使得图像杂乱无章,达到加密目的。用于这类的混沌映射主 要 有 Arnold 变 换、Baker map[10]、Cat map[11]、Tent map等。图像像素值变换的加密方式也称置混方法,是通过使用混沌系统生成伪随机流,将随机流直接掩盖明文,改变原图像各像素点的像素值,使攻击者无法辨认原始图像,从而达到对图像加密的目的。用于这类加密的混沌系统有 Logistic映射、PWLCM映射、Chebyshev映射、Henon映射、Lorenz系统、Chen系统等。Logistic映射因具有实现简单的优势,可以设计出实现速度较快的密码系统而得到广泛的应用[2-5]。但Logistic映射不总是能产生混沌序列,如何保证Logistic映射产生出混沌序列是将Logistic映射用于图像加密的关键。另外,混沌系统是基于实数集的,而加密在整型的离散集中进行,所以基于混沌的数字图像加密方法均需对混沌序列做取整形化处理,而这一处理会导致动力学特性的退化。因此,基于Logistic映射的图像加密还需要进一步的研究。本文通过分析Logistic映射所产生序列的随机特性,指出了这种混沌序列实际用于加密时存在的安全隐患问题以及避免这些加密安全隐患的规则。
1 Logistic混沌映射
Logistic映射是一种非常简单却被广泛应用的经典动力学系统,其模型可被定义如下:

式中,μ∈(0,4],xn∈[0,1],解方程 f(xn)=μxn(1-xn)得到 2个平衡点:x1=0,x2=1-1/μ。由于不动点线性部分的雅可比行列式J=f/x=μ-2μx,可知系统的稳定性取决于参数μ。目前研究者已得出以下结论:
当 1<μ<3,不管 x0取什么初值,在 n→∞,xn=1-1/μ是稳定的。
当 3<μ<3.449,在 n→∞,式(1)存在 2个平衡点。
当 3.449<μ<3.544,在 n→∞,式(1)存在 4个平衡点。
1.8 统计学处理 应用 GraphPad Prism 5.0 软件进行数据处理和统计学分析。呈正态分布的计量资料以±s 表示,两组间比较采用两独立样本 t检验,多组间比较采用单因素方差分析(one-way ANOVA)。检验水准(α)为 0.05。
当 3.544<μ<3.564,在 n→∞,式(1)存在 8个平衡点。
随着 μ 值的增加,出现稳定的 1,2,4,6,8,16,…,2n周期点,但当 μ∈(3.569 9…,4]时则周期 2n轨迹不再存在,进入混沌区[2-3,6-7,12]。在这一混沌区具有对初值极端敏感和非周期等特点,所以常被研究者用来加密图像,并把初值x0和参数μ用来当作密钥。
当μ=4时,式(1)进入最佳混沌状态而且序列值能填满[0,1]区间的实数,具有遍历性,是加密的最好参数取值[4]。
2 Logistic混沌序列用于图像加密的安全隐患分析
2.1 Logistic混沌序列的整型化问题
Logistic产生的是0~1之间的实数,而图像值是一个整数。若先将图像像素值转为如参考文献[7]的实型,则会因为不同系统对浮点数运算的精度抖动,而出现在一个平台上加密无法在另一个平台解密的现象。若将实型混沌序列转为整型序列,则要将所有序列值扩大K倍。因为Logistic混沌序列很多小数点后前几个数都是相同的,如果扩大的倍数不够大,则混沌序列将丧失混沌性质,这时加密出来的的图像是很不安全的。在Logistic模型中当μ=4时,完全呈现混沌状态而且序列值能填满[0,1]区间的实数,具有遍历性,是加密的最好参数取值[4]。但若在处理序列值实型转为整形时采用扩大倍数方式时,若扩大倍数K取值不够大,则加密效果极差。如图1加密效果对比中的图1(a)是加密前的Lena原图,图1(b)为 μ=4、K=100时加密后的密图,从密图中仍可看到加密前Lena图的原始信息,并没有达到加密效果,此时混沌序列已丧失混沌特性。而当扩大倍数K的取值足够大时,则不会导致混沌特性丧失,如图1(c)为μ=4、K=105的密图,它已是面目全非了,攻击者无法辨认原始图像,从而达到了对图像加密的目的。所以,参考文献[2]中将扩大倍数K作为密钥中的子密钥而又没有规定K的最小取值是不合理的做法,加密者可能会选到过小的K值而使混沌序列丧失混沌性,而导致加密算法的安全性无法得到保障。

图1 不同的整型化因子下的加密效果对比
2.2 Logistic映射参数μ的取值与周期性窗口
目前学者认为,当 μ进入(3.569 9…,4]区间时,Logistic 序列就进入混沌区[2-3,6-7,12],但本文通过实验发现,当μ取3.835时只有3个稳定值,取3.845时有6个稳定值,经大量实现测试发现,μ在[3.828,3.875]之间取值均存在周期性,μ取 3.583、3.63、3.74等也出现周期性。图2(a)表示序列值 xn与参数μ在 1~4之间的分岔图,此图还看不出参数μ在(3.569 9…,4]区间有周期窗口,但从图2(b)xn值与参数μ在3.5~4之间的分岔图中则可清楚地看到:当 μ进入(3.569 9…,4]区间内 μ的取值处确实出现了一些周期性很强的窗口,即周期窗口。所以,虽然 μ∈(3.569 9…,4]属于混沌区域内,但并不意味着在这一区域仅存在混沌轨迹[10],μ在窗口中的取值使Logistic映射所产生的序列是周期性序列而不是混沌序列,因此,将该序列用于数字图像加密时会严重影响到加密的效果,算法加密的安全性完全无法保障,对图像进行置混后得到的加密图像都还可以看到原始图像的情况。如图3是采用了参考文献[2]中用到密码反馈机制的较好加密算法对Lena进行加密的密图,从密图仍可识别原图为Lena图。所以用Logistic映射加密图像时把μ作为子密钥是不合理的。
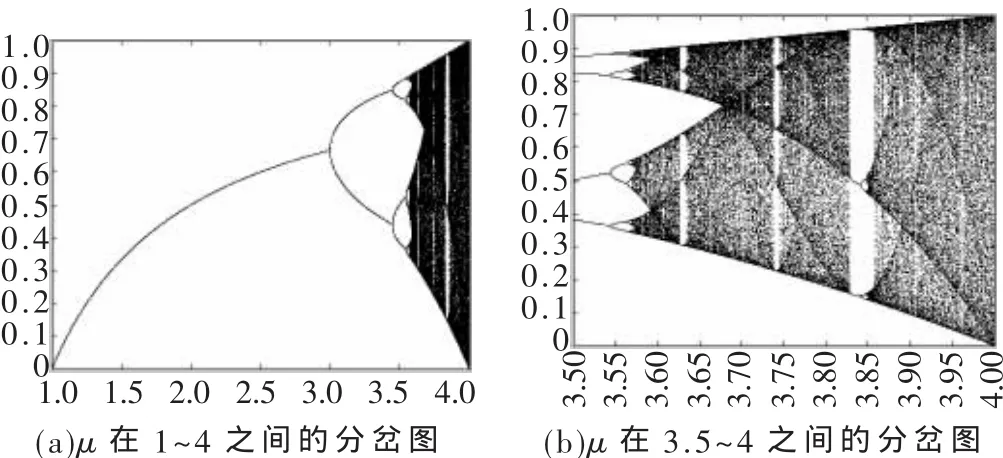
图2 Logistic映射分岔图
3 Logistic映射用于图像加密规则
针对上述问题,本文给出避免加密安全隐患的3条规则:

图3 μ取到周期点时加密效果图
规则1:不能把参数μ作为密钥。2006年,ALVAREZ G和LI Shu Jun针对混沌密码学的安全要求提出了具有代表性的17条建议规则[13]中指出:密钥空间 к中的所有选择都应是有效的密钥,密钥空间к应明确规定而且应避免非混沌区域。而本文上面已说明μ∈(3.569 9…,4]区间内存在着一些周期窗口,而μ的取值为实型,无法将所有呈现出周期性的点彻底排除在外。所以,为了保证算法的安全性不能把Logistic映射的参数μ作为密钥,加密算法应该确定μ的取值,保证整个映射具有很好的混沌特性。
规则2:如果要把扩大倍数K作为密钥的一部分,为保证原混沌序列不丧失混沌学特性,应先求出K的最小取值Kmin,加密时明确规定K取值的下限为Kmin。
求解Kmin的主要算法如下:
(1)确定式(1)中的 μ值(保证该取值不在非混沌区)得到:

(2)用式(2)生成的混沌序列1:
x0,x1,x2…xi,xj,…xn
(3)排序得到序列 2:
y0,y1,y2,…yi,yj,…yn
(4)yk-yk+1,k=0,1,2,…,n,即求序列 2 中两相邻值之差最小的值min。
(5)计算出min的小数点到小数点后第1个非零数之间的零的个数 m,则Kmin就为 10m+1。
规则3:用 Logistic映射对图像进行置混加密时,应该与置乱方法结合。
随着计算机计算速度的增加,密码学的安全要求也越来越高,为了能抵抗蛮力攻击,密钥空间к应该大于2100[13]。而若单独用Logistic映射进行加密,经上述分析不能把参数μ作密钥,就大大减小了密钥空间。若只用初值x0作为密钥,从理论上有无限大的密钥空间,但由于当前计算机有效位数的限制,若取15位有效数的话,其密钥空间为1015约为250<2100,无法满足当前的安全要求。所以用Logistic映射对图像进行置混加密时,应该与置乱方法结合来增加密钥空间以保障加密算法的安全性。本文建议与一些相对简单的置乱方法,如Arnold变换、Baker map变换、Cat map变换等相结合。因为现代密码学要求在不损失安全的前提下,加密系统的设计应尽可能地满足低成本和执行速度快的要求[11]。
本文总结了Logistic映射目前已有的一些结论,分析了在采用Logistic映射对图像进行加密时常被很多文献所忽略的一些安全隐患问题,并通过实验证实了这些安全隐患所带来的危害性。同时给出了避免加密安全隐患的3条规则,这3条规则对基于Logistic映射的数字图像加密能起到保证加密安全的作用。
[1]PENG Jun,ZHU Shang.A novel scheme for image encryption based on piecewise linear chaotic map[C].2008 IEEE Conference on Cybernetics and Interlligent Systems, 2008∶1012-1016.
[2]彭成等,柳林.基于混沌序列的压缩图像加密算法[J].计算机工程,2008,34(20)∶177-179.
[3]刘树堂,孙福艳.基于空间混沌的图像加密设计[J].中国科学,2009,39(3)∶387-393.
[4]HONGE R,ZHENWEI S.A chaotic algorithm of image encryption based on dispersion sampling[C]//proceedings of the 8th International Conference on Electronic Measurement and Instruments, 2007∶836-839.
[5]ZHANG Yun Peng, ZUO Fei, ZHAI Zheng Jun, et al.A new image encryption algorithm based on multiple chaos system[J].International Symposium on Electronic Commerce and Security10.1109/ISECS,2008,142.
[6]贺文华,朱从旭.基于双混沌映射的快速图像加密新算法[J].计 算 机 工 程 与 应 用,2008,44(7)∶152-154.
[7]HONG Lian Xi,LI Chuan Mu.A novel color image encryption approach based on multi-chaotic system[C]//proceedings of the 2nd International Conference on Anti-counterfeiting, Security and Identification, 2008∶223-226.
[8]PISARCHIK A, CARMONA N F, VALADEZ M C.Encryption and decryption of images with chaotic map lattices[J].Chaos,2006,16(3).
[9]蔺兢,吴立伟.基于混沌的图像空域复合加密方法的研究[J].电脑开发与应用,2008,21(9)∶29-31.
[10]SALLEH M, BRAHIM S I, ISNIN I F.Enhanced chaotic image encryption algorithm based on chaotic maps[C].IEEE Conf Circuits and Syst, 2003∶508-511.
[11]CHEN Guan Rong, MAO Yao Bin, CHARLES K C.A symmetric image encryption scheme based on 3D chaotic catmaps[J].Chaos,Solitons&Fractals, 2004,21(3)∶749-761.
[12]丁文霞,卢焕章.基于混沌系统的独立密钥DES数字图像加密算法[J].计算机应用研究,2006(2)∶113-115.
[13]ALVAREZ G,LI S.Some basic cryptographic requirements for chaos-based cryptosystems[J].chaos, 2006,16∶2129-2151.

