植树护岸对河道水流影响的数值模拟

程 莉,赵振兴,黄本胜

(1.河海大学力学与材料学院,江苏南京 210098;2.广东省水利水电科学研究院,广东广州 510610)

植树护岸对河道水流影响的数值模拟

程 莉1,赵振兴1,黄本胜2

(1.河海大学力学与材料学院,江苏南京 210098;2.广东省水利水电科学研究院,广东广州 510610)

利用局部精细模拟的二维有限元数学模型对植树护岸条件下河道的水流特性进行模拟分析,结果表明:局部精细模拟更能有效考虑形状阻力,真实反映树干对流场的影响,植树后,植树区域的流场产生旋涡,并在局部地区产生滞水区,滩地的过流能力减小,主槽的流速增加,过流能力加大,并且对水位的影响小。数学模型的计算结果与实验所观测的变化规律相一致。

植树护岸;河道水流;数值模拟;有限单元法

水利工程中的岸坡濒临江河湖海,因长期受到自然变化、环境侵蚀等多种因素影响而遭受不同程度的破坏,从而使工程效益下降。为了更好地发挥水利工程岸坡的作用,应采取措施护岸。护岸的形式主要有工程护岸和植物护岸两类。大多数的岸坡都可以采用植物防护的方法。长期实践证明[1-2],在堤外滩地种树,利用树根保护土壤,避免水土流失,是固滩固岸行之有效的方法。然而,河滩种树可能会增大滩地的糙率,从而减小整个河道的行洪能力。因此对于河滩种树这种生物护岸措施,要研究如何因地制宜合理种植,既最大限度地发挥其固滩护堤的作用,充分地利用滩地资源,又能确保行洪安全,这对于生产实际具有积极的指导意义。

目前国内外主要采用等效糙率或附加阻力等方法[3-4]来模拟类似于树干、码头桩群、桥墩等阻水物的阻力问题,而这类方法不能有效反映形状阻力的影响,因此计算得到的阻水物附近流场是失真的。为真实反映树干对流场的影响,笔者对每根树干的几何形状进行了精细模拟,计算网格中将树径为0.24 m的圆形树干按其轮廓概化为六边形来处理(如图1),这样能有效地考虑形状阻力。由于树干形状模拟的边界复杂,笔者采用具有网格剖分灵活、精度高、便于复杂边界处理的二维有限单元法[5-7],分析计算植树护岸对河道水流影响,并将数模计算的结果与实测值进行对比分析。笔者的研究可为树干、码头桩群、桥墩等阻水物的数值模拟提供借鉴。

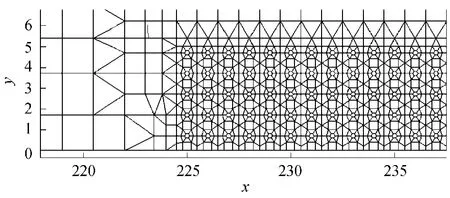
图1 种树段细部网格剖分

1 数学模型的建立

静水压强假定下,沿水深平均的二维流动基本方程(1)～(3)[8]:

式中:h为水深;zb为河床高程;u、v分别为沿水深平均的x、y方向流速;f为柯氏力系数;ψ为当地纬度;ω为地球自转角速度;τzxb、τzyb为底部摩阻力;c为谢才系数;n为糙率;τzxs、τzys为风生分应力;cw为风的阻力系数;ρa为空气的密度；为风速;α为风速与y轴的夹角;τxx、τxy、τyx、τyy均表示沿水深平均的偏斜应力。

笔者采用的二维水流基本方程是将连续方程式(1)由非线性方程转化为线性方程,即是将速度项转为单宽流量:令U=hu,V=hv;并令Nij=hτij,将沿水深平均的水平向有效应力τij转化为单宽水平有效应力Nij,对于单宽水平有效应力Nij,采用紊流中涡黏性方法分析[9]。引入涡黏性系数 ε,涡黏性系数 ε中既包括了分子黏性(与温度有关,为均匀各向同性),又包括了紊动黏性(为非均匀各向同性)。所以ε在整个计算区域中不是常数。在有限元计算中,可以令ε值在每个单元内是常数,当单元数趋于无穷大时,可认为ε是连续分布的。对于任意单元内,ε为常数。将单宽流量U、V以及单宽水平有效应力Nij代入式(1)～(3),可得出静水压强假定下,笔者采用的不可压水体二维流动的基本方程(4)～(6):

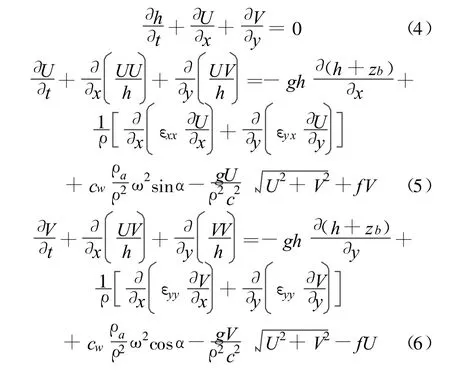
2 数值方法和定解条件

2.1 方程的离散及求解

有限元方程是通过二维水流运动方程进行离散得到的。二维水流运动方程空间域上的离散采用有限单元法,笔者采用Galerkin有限元法将浅水方程离散成非线性代数方程组,然后采用牛顿-拉斐逊迭代法对非线性方程进行求解,离散区域内采用三角形六节点的等参单元或四边形八节点等参单元;浅水方程在时域上采用差分离散。

2.2 定解条件

边界条件分为开边界和闭边界两种。开边界以流速或水位的形式给出。闭边界采用不可入原理,法向速度为零。计算开始时,计算区域内各点的水位值、流速值必须给定。一般采用“冷起动”的方法,即给定各点一个平均水位和零流速作为初始条件。由于初值问题方程的解由边界条件控制,所以,初始值的影响最终会消失。

3 数值模拟及结果分析

3.1 模型的范围及其边界条件

根据广东省水电科学研究所模型试验[1],对河长600m具有单边滩地复式河道进行数值模拟(断面如图2),种树带长150m,树径0.24m,树与树之间的间距和行距为1m×1m的正方形排列方式,计算网格中将圆形的树干按其轮廓概化为六边形来处理,在种树段(x=225～375m)采用局部加密的方法适应细部边界的变化(如图1),为了使相邻网格尺寸变化不至过大,在种树的滩地与主槽和没有种树的滩地之间采用尺寸逐渐变化的过渡网格,以提高精度。模型所需要的开边界条件为上游给定流量、下游给定水位。

图2 单边滩地复式断面示意图

3.2 验证计算

为了对所建数学模型的可靠性进行验证,根据广东省水电科学研究所模型试验研究报告的试验结果,分别取3组情况进行验证计算:①流量为430.00m3/s,水位为7.2m;②流量为485.56m3/s,水位为7.8m;③流量为544.71m3/s,水位为8.4m。种树前后物模试验结果及数模计算结果比较见图3。由图3可知,数模计算结果与物模试验结果基本一致,说明数值模型计算的水流反映了实际水流运动情况,笔者采用的方法可行,网格剖分合理,计算程序可靠。

图4 种树段进口及出口附近流场

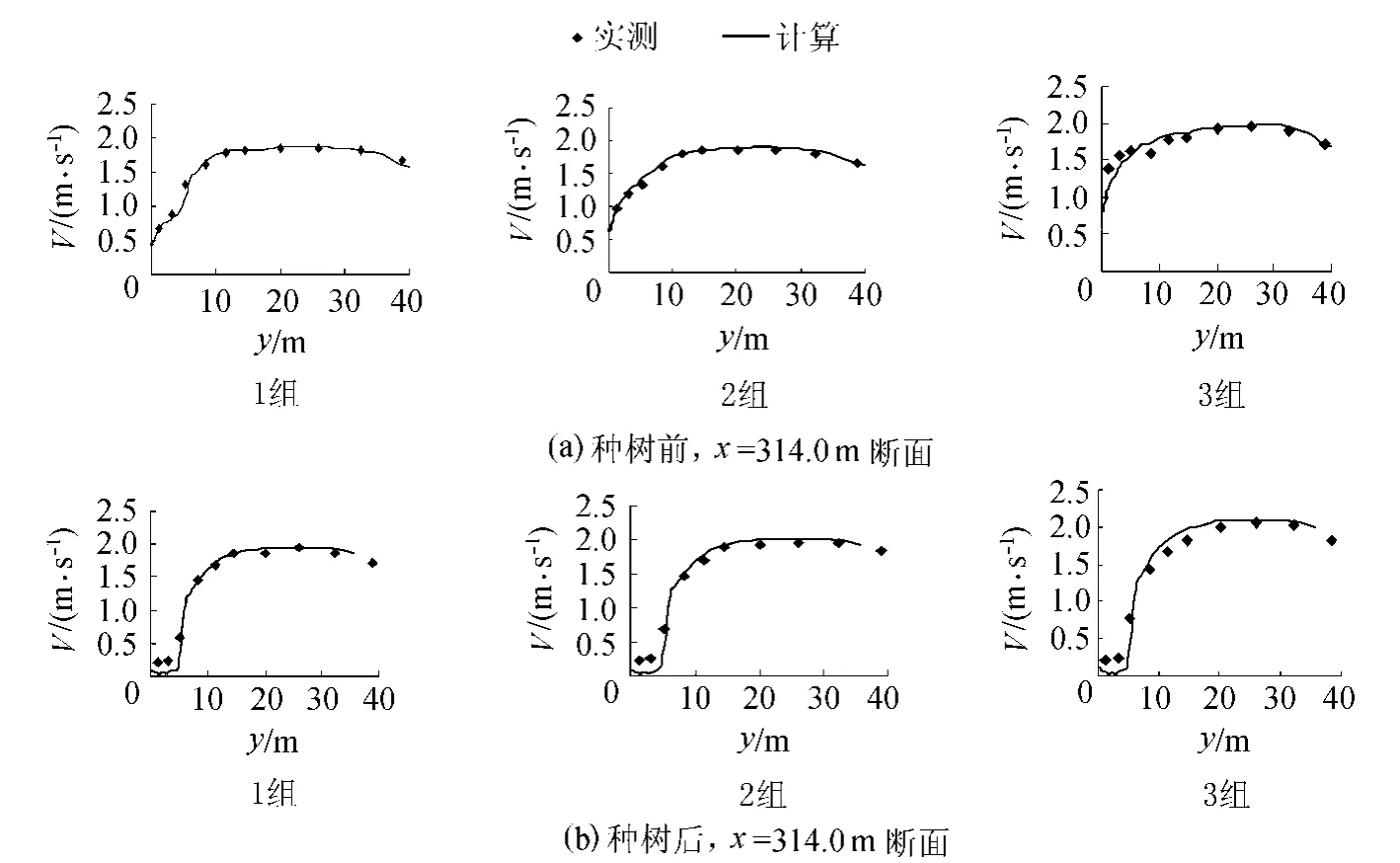
图3 种树前后物模和数模计算结果比较

3.3 计算结果分析

3.3.1 流场分析

分别对3组边界条件下种树前后河道内的流场进行计算,用以分析植树后树群对流场的影响。流场见图4。由图4可见:在种树带的前端(x=225.0m)附近,由于树的形状阻力的增加,靠近主槽的区域附近的滩地水流偏斜流入主槽,其流向由滩地向主槽发生偏移,这种滩地上的水流流向发生偏移的范围逐渐地向岸边发展,滩地流速的衰减规律是:靠近主槽的滩地流速衰减得快,而远离主槽的滩地流速衰减得慢,往下游一段距离在滩槽交界处出现旋涡(图4(a));滩地上种树区域的流速由种树带前端往下游一定范围内出现较大的衰减,到达一定距离后,流速接近于0,滩地上形成一段滞水区域(图4(b));继续往下游,由于滩槽交界处旋涡的作用,上游主槽水体有一部分进入到滩地,在滩地的种树带区域内形成旋涡区(图4(c));这种滞水区域与旋涡区交替出现的现象持续到种树段出口附近(图4(d));在种树段出口处,由于滩地上再无树群的阻碍,滩地的阻力减小且过流能力增加,因此出现水流流向由主槽向滩地偏移的情况(图4(e))。

图5 种树前后横断面流速分布比较(x=310.0m)

3.3.2 流速变化

复式断面河道,由于滩地水深小于主槽水深,因此滩地的流速低于主槽的流速,而对于滩地上种树的复式断面,其滩槽流速差值就更大,图5为种树前后横断面流速比较。由图5可知:滩地种树后,滩地流速明显减小,滩地与主槽交界附近的流速有一定的减小,主槽区域流速增加。

种树后的流速分布不仅在横向上有变化,沿纵向也有变化。图6为滩地断面平均流速Vf沿程分布情况。模拟和实验结果均显示,滩地平均流速在进入种树区域后出现衰减,到达种树段出口附近,流速出现增长,滩地平均流速恢复到与种树段前的流速接近。出现这样的流态,是由于滩地种树后增加的形状阻力阻碍了种树段的水流流动,造成种树段流速大幅度减小。

图6 滩地断面平均流速沿程分布

3.3.3 主槽流量变化

滩地种树后,由于种树段滩地阻力远大于主槽的阻力,水流进入到滩地后,受到树的形状阻力的作用,促使水流从滩地流向主槽,从而增加了主槽流量。图7为主槽流量与河道总流量之比沿程分布情况。由图7可知,主槽流量在种树段明显增加。

图7 主槽流量与河道总流量之比沿程分布

3.3.4 水位变化

图8为滩地种树前后水位沿程变化的情况。图8表明:在种树段进口附近及其上游的一段距离内水位壅高;其后至种树带出口附近水位降低;种树带出口下游一段距离后,水位变幅为0,即种树前后的水位一致。总体而言,种树前后水位沿程变化的幅度不大(ΔZ＜±1 cm),滩地种树对水位影响不大。此现象主要归结于,种树段进口附近水位壅高是由于滩地种树后,河道的过水面积减小,相当于河道断面缩小的情况,水面线会出现壅高,而其后至种树带出口附近,由于种树带的形状阻力的存在,导致水流在运动过程中消耗能量,因而水位低于种树前的水位,到达种树带出口下游一段距离后,水流不再受到种树带的影响,水位恢复到种树前的水位。

图8 滩地种树前后水位差沿程变化

4 结 论

笔者采用局部精细模拟的二维有限元数学模型对植树护岸条件下河道的水流特性进行了模拟分析,计算结果和实测数据比较表明:数值模型和计算程序是可靠的。对每根树干的几何形状进行精细模拟更能有效考虑形状阻力,真实反映树干对流场的影响。通过对多组试验结果的数模计算分析得出植树护岸条件下河道水流的特性:①滩地种树使滩地水流偏斜进入主槽,并在滩地上形成滞水区域,滩地与主槽交界处有旋涡;②滩地种树使滩地流速减小,主槽流速和主槽的过流能力增加;③滩地种树对水位影响不大。

[1]黄本胜,赖冠文,邱静,等.河滩种树对行洪影响实验研究[J].水动力学研究与进展,1999,14(4):468-474.

[2]PASCHE E,ROUVE G.Overbank flow with vegetatively roughened flood plains[J].Journal of Hydraulic Engineering,1985,111:1262-1278.

[3]唐士芳,李蓓.桩群阻力影响下的潮流数值模拟研究[J].中国港湾建设,2001,10(5):25-29.

[4]李光炽,周晶晏,张贵寿.高桩码头对河道流场影响的数值模拟[J].河海大学学报:自然科学版,2004,32(2):216-220.

[5]程莉.植树护岸条件下河道水流的数值模拟[D].南京:河海大学,2002.

[6]刘希云.流体力学中的有限元与边界元方法[M].上海:上海交通大学出版社,1993.

[7]KING I P,NORTON W R,ICEMAN K R.A finite element solution for two-dimensional stratified flow problems[C]//Finite Elements in Fluids.New York:John Wiley&Sons,1975.

[9]何少苓,WARREN I R.平面二维明渠流动数值计算中涡黏性系数项的合理选取[J].水利学报,1990(4):1-10.

Numerical simulation of effect of trees planted in floodplain on water flow pattern in river

CHENG Li1,ZHAO Zhen-xing1,HUANG Ben-sheng2
(1.College of Mechanicsand Materials Science,Hohai University,Nanjing 210098,China;2.Guangdong Research Institute of Water Resources and Hydropower,Guangzhou 510610,China)

A two-dimensional finite element model with a local refined grid simulating a tree trunkwas applied to simulate and analyze the water flow characteristics in a river channel,where trees were planted on the river bank.The results indicated that the shape resistance of the trees could be more efficiently considered with the local refined grid,and the effect of tree trunks on the flow field was factually shown by the simulation.With planted trees,vortices formed in the planting zone.Meanwhile,a water stagnation zone formed in some areas.Flow capacity in the floodplainwas reduced by planted trees,while the flow rate and flow capacity in the main channel increased.The planting had little effects on the water level.The computational results correspondedwith the experimental measurements.

revetment with planted trees;river flow;numerical simulation;finite element method

TV133.1

A

1004-6933(2010)02-0024-04

国家自然科学基金(50638020)

程莉(1974—),女,贵州惠水人,讲师,博士研究生,主要研究方向为计算水力学、生态水力学。E-mail:chengli7853@163.com

(收稿日期:2009-09-01 编辑:徐 娟)