宜万铁路落步溪大桥提篮型拱肋钢管骨架吊装方案计算

陈 强,王树国,彭学理,黄鸿建

(1.中国铁道科学研究院铁道建筑研究所,北京 100081;2.铁道部宜万铁路建设指挥部,湖北恩施 445000)

宜万铁路落步溪大桥提篮型拱肋钢管骨架吊装方案计算

陈 强1,王树国2,彭学理2,黄鸿建2

(1.中国铁道科学研究院铁道建筑研究所,北京 100081;2.铁道部宜万铁路建设指挥部,湖北恩施 445000)

运用“改进的有限元零位移法”进行了落步溪大桥提篮型拱肋钢管骨架扣索索力优化计算,得出了合龙前钢管骨架的一组最优扣索索力。在本组扣索索力作用下,钢管骨架的线形(高程、中线)最大误差小于2mm。骨架结构的倒拆计算结果表明,本组最优化扣索索力不仅能够满足钢管骨架正装过程中结构的强度安全及稳定性要求,而且能够给出骨架安装过程中的线形、钢管应力、索力控制值以指导施工。骨架成型后的线形、应力实测值与理论计算值对比分析证明,本方法不仅能够保证骨架具备较高的合龙精度,而且可以避免吊装过程中的调索难题,是一种可靠有效的钢管骨架吊装控制方法,对同类型桥梁的施工具有一定的工程指导意义。

宜万铁路;提篮拱;钢管骨架;吊装控制;优化;监测

1 工程简况

落步溪大桥为国内跨度较大的钢管混凝土劲性骨架提篮拱桥。由于大桥地处山区,山坡陡峻,河谷深窄,为一孔跨越深谷,主桥采用跨越能力较强的拱桥(矢跨比确定为1/4.5),孔径布置为1 -24m后张梁+1-178m上承式拱桥+1 -32m后张梁,桥型布置见图1。

本桥两岸边坡陡峻,拱圈施工是本桥施工的关键。主跨178m上承拱桥拱圈的施工结合地形条件,采用了裸拱合龙相对容易的劲性骨架混凝土拱圈方案,以减小大跨度桥梁的施工风险。为了增强其横向稳定性,拱肋为提篮型布置。178m上承式钢筋混凝土拱肋的拱轴线为悬链线,采用单箱单室箱形变高度截面[1]。骨架空钢管的吊装是本桥施工的重点工序,也是风险较大、施工较困难的工序之一。它不仅关系到混凝土拱肋成型的质量,也对拱肋混凝土外包施工,拱上立柱、拱顶框架及拱上连续梁的施工有着重要的影响。由于地形条件的限制,本桥采用无支架缆索吊装方案架设拱肋钢管骨架,为保证骨架安装过程中的安全及骨架的顺利合龙,进行了扣索方案的优化计算,并结合合龙前的温度效应计算结果,给出了合龙前的扣索索力优化值、骨架吊装过程中高程、钢管应力、扣索索力控制值以及合龙施工的相关建议。

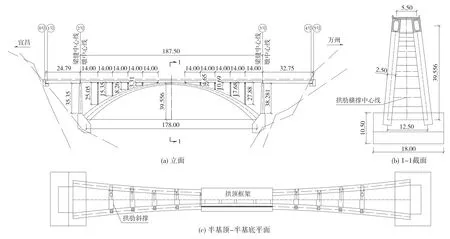
图1 落步溪大桥总体布置(单位:m)

2 钢管骨架吊装过程扣索索力优化模型及迭代算法[2～5]

对钢管混凝土拱桥而言,拱肋吊装过程的控制是确保拱肋成型质量的重要工作[6]。随着计算技术的发展,有限元法越来越多地应用于钢管拱肋节段吊装过程控制的理论计算中,并取得了较好的工程应用效果。该方法在建立有限元模型时是以考虑了预拱度后的设计拱轴线作为模型的线形标准,并直接在索的扣点处施加零位移支座约束(竖向和纵向)来模拟扣索的约束,这样在计算出扣点的支座反力后,直接将支座反力进行合成来作为各拱肋节段吊装中的扣索索力或索力增量。由于各拱肋节段吊装后所有扣点的位移始终假定为零,故该方法又称为“零位移法”。根据此原理,细致分析后可发现此方法存在着一定的缺点:(1)在拱肋节段吊装阶段,各扣点的约束水平反力增量与约束竖向反力增量无法保持一致,通过约束反力合成的索力增量方向是不断变化的,这与扣索的水平基角基本不变的实际情形不相吻合;(2)通过约束反力合成的索力有可能出现负值,即索力方向指向拱肋内部,而扣索只能承受拉力,不能承受压力,因而可能会出现求出的各组索力无效的现象;(3)采用该方法求出的索力只能保证扣点处的高程满足设计要求,其他位置的高程无法控制,拱肋线形会出现波浪形的偏差,影响其内力状态;(4)当实际施工线形与理想线形存在偏差时,该方法不能求出线形调整时索力的实时调整量,影响施工进度。

针对上述传统的“零位移法”计算扣索索力的缺点,笔者提出不再考虑扣索对骨架节点的约束作用,而是将扣索模拟成索单元(考虑非线性后成为弹性悬索结构)参与整体结构的分析,经过非线性迭代计算,识别出骨架合龙前一组最优扣索索力,并进行骨架结构的正装计算和倒拆计算,判定该组最优索力能否满足拱肋骨架的正装和倒拆要求(结构的强度安全及稳定性),当求出的一组扣索索力满足施工过程中的安全、稳定、强度要求后,利用倒拆计算给出骨架安装过程中的高程、应力、索力控制数据,用于指导施工。

2.1 索力优化分析的数学模型

求解扣索索力的优化模型可采用下面的数学形式进行描述。对钢管拱肋骨架的某吊装阶段,用 MIDAS-Civil建立力学正问题的有限元控制方程[7]

式中 K——结构的整体刚度矩阵;

u——节点位移向量;

F——结构自重、施工荷载及温度荷载等产生的节点等效力向量。

显然,由式(1)可知,对于某特定的吊装节段,拱的位移u是关于索力向量S的函数,即u=u(S),因此求解索力的问题可转化为如下有约束的极小值问题

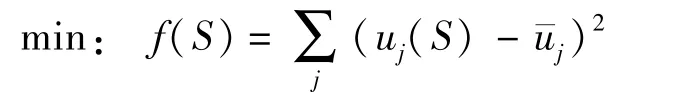
其中:S=[s1,s2,s3,…,sN]

使得:

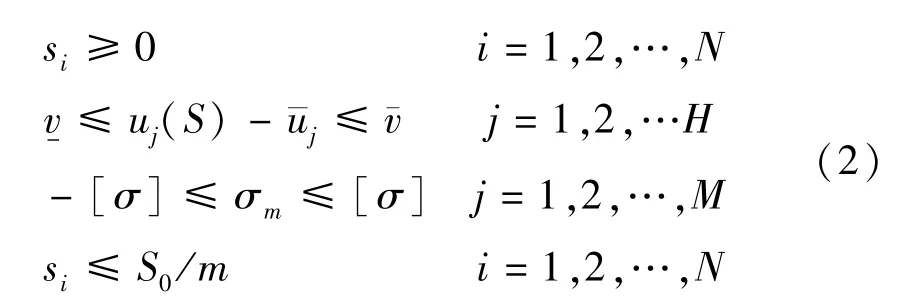
其中:f—目标函数,S—设计变量,uj、σm—状态变量。式(2)中各符号的意义如下:si—i号扣索的索力张拉值;S—所有扣索索力组成的向量;uj(S)—拱肋第j个高程控制点在F作用下的竖向位移值,此值由结构有限元分析得到;¯uj—j控制点的期望预拱度,为已知量; ¯v、v-—施工中拱肋高程允许偏差的上、下限;σm—第m个内力控制截面的最不利Mises应力值,由有限元计算得到;[σ]—为钢管的容许应力;N—扣索的总数; H—高程控制点的总数;M—内力(或应力)控制截面的总数;S0—索的容许应力;m—索的安全系数。

从式(2)显示的意义可知,理想的情况是通过张拉扣索,使拱轴线全盘达到期望线形,即f(S)=0,但实际上这是无法做到的。因为期望预拱度值主要与钢管的自重以及温度荷载有关,它是分布载荷,而扣索索力值为点荷载,因此索力优化计算中必须选取若干高程控制点。当迭代优化的索力能保证H个高程控制点的f(S)最小,并且各单个控制点的高程及骨架内力(或应力)偏差满足相关规范和设计要求,此时得到的索力为最优索力,相应的拱肋线形也是最逼近期望的线形。高程控制点数H越大,拱肋线形越符合期望线形。

当然,通过合龙前某一施工阶段的扣索优化计算得到的一组索力,未必能够满足骨架倒拆计算和正装计算的要求,因而有必要进行骨架的倒拆计算。如果优化计算得到的索力不能满足倒拆计算和正装计算的要求,则选择不能满足骨架正装计算的施工阶段进行适当的调索计算。

2.2 索力优化分析的计算迭代步骤[7～8]

第1步:选定合龙前某一阶段(一般为合龙前的最不利阶段),设定1组索力(S0),并考虑自重(w)、临时荷载(L)等可能荷载进行结构的正分析,计算出结构的位移(u1)、应力(σ1)、索力(s1)。

第2步:判定第1步计算结果是否满足拱肋骨架线形、应力、索力的控制要求即

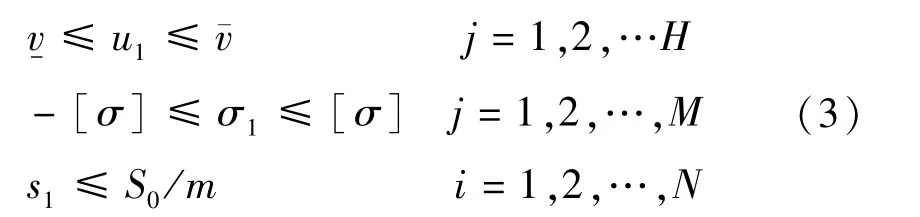
如果式(3)不满足,则将索力s1代入第1步重新计算,直至满足要求,得出1组最优索力si;如果式(3)满足,则直接进入第3步。

第3步:以si为优化索力,进入倒拆计算,第j阶段的倒拆计算结果为sj,uj,σj(j=1,2,…,k,k为倒拆计算工况数),判定sj,uj,σj(j=1,2,…,k)是否满足结构的安全、稳定要求,即

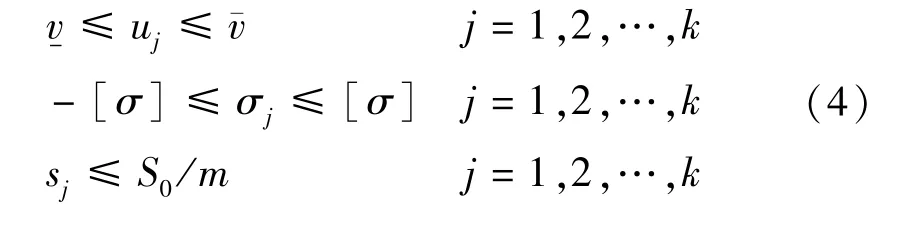
如果式(4)成立,则si为满足正装计算和倒拆计算要求的一组可行最优化索力,输出倒拆计算结果(o—表示优化索力作用下计算结果,k—第k个倒拆计算工况),即本组结果可以作为一组优化扣索索力作用下骨架正装施工过程中的控制数据。如果式(4)不满足,则进入第4步。

第4步:以si为优化索力,进入倒拆计算过程中的调索计算,选定第3步中不满足式(4)的工况(假定为M工况),进行调索优化,使得调整后的索力工况M能够满足式(4),输出M工况的索力变化量ΔSm,以及本工况下的位移、应力结果um,σm以作调索时参考。

根据笔者的经验,上述迭代计算一般需要5～8次循环,而且一般情况的最优优化索力均能满足拱肋骨架正装计算及倒拆计算的要求,较少遇到在吊装过程中需要调索的情况,依据本文中的扣索索力优化计算方法得到的优化索力不仅能够满足正装计算和倒拆计算的要求,而且保证了吊装过程的一气呵成,在不需要任何调索工作的前提下,骨架即可具备良好的合龙条件,保证了合龙施工的顺利及良好的骨架应力状态。

3 落步溪大桥钢管骨架吊装方案计算结果及分析

受落步溪大桥的施工场地条件限制,采用传统的扣塔-扣索法安装骨架较为困难,经过方案比选,最终选择了无扣塔扣索方案,即扣索后锚点充分利用本桥拱座后方的桥台(进行相应的预应力配束),扣索编号见图2。整桥钢管骨架共分为11段,宜昌侧和万州侧各5段。11号节段为合龙段。根据实际采用的吊装过程,每一节段安装定位后,即张拉相应编号的扣索,随后继续安装相应的钢管节段并张拉相应扣点处的扣索。MIDAS计算模型见图3。

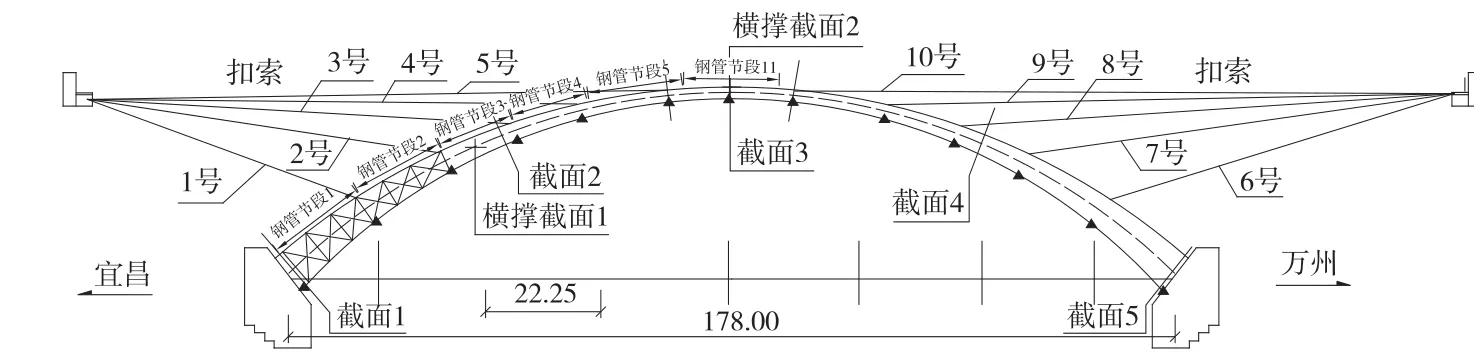
图2 落步溪扣索方案简图及扣索编号(单位:m)

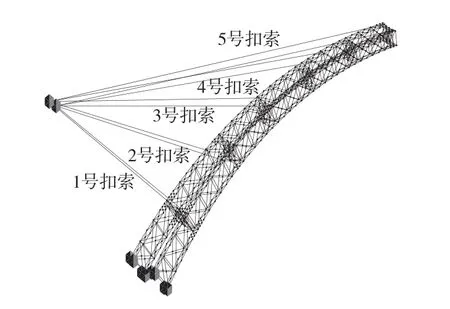
图3 索力优化计算模型

3.1 钢管骨架的变形计算结果及分析

在最优扣索索力作用下,骨架结构的变形见图4。拱肋骨架节点最大竖向位移为3.36mm,最大纵向位移为-30.2mm,合龙处拱肋上、下弦节点纵向位移分别为:-9.9、-8.9mm。二者相差约1mm。

3.2 扣索索力及骨架结构应力

经过多次迭代计算,合龙前的最优扣索索力计算值见表1。

图4 一组优化扣索索力作用下骨架变形等值线

表1 优化后的扣索索力值 N

在本组优化索力作用下,合龙前拱肋钢管骨架最大压应力-34.54MPa,最大拉应力为17.34MPa,均低于相应的强度容许应力及稳定承载力,即该组索力能够保证合龙前钢管骨架结构的强度及稳定性。

3.3 钢管拱肋骨架吊装过程坐标控制值计算

在最优扣索索力作用下,通过倒拆计算,得出各节段安装过程中扣点对应的下弦钢管节点坐标控制数据,供吊装施工控制时参考(表2)。需要说明的是,每一节段吊运就位后,只需要控制该节段吊点位置处的坐标,其他位置处的测试值仅作校核。由表2中的数据可知,吊装3号节段、4号节段时,扣点竖向坐标分别要求与理论坐标相差-14.6、-37.8mm,而当5号节段吊装完成即5号扣索张拉值控制索力值后,骨架各节点竖向坐标与理论坐标最大差值仅为-2.1mm。由于本桥的扣索后锚点的高程低于拱肋骨架最高点,因此随着节段的吊装,骨架的顺桥向压缩量逐渐增大,合龙前5号扣点的最大轴向压缩量为8.9mm。

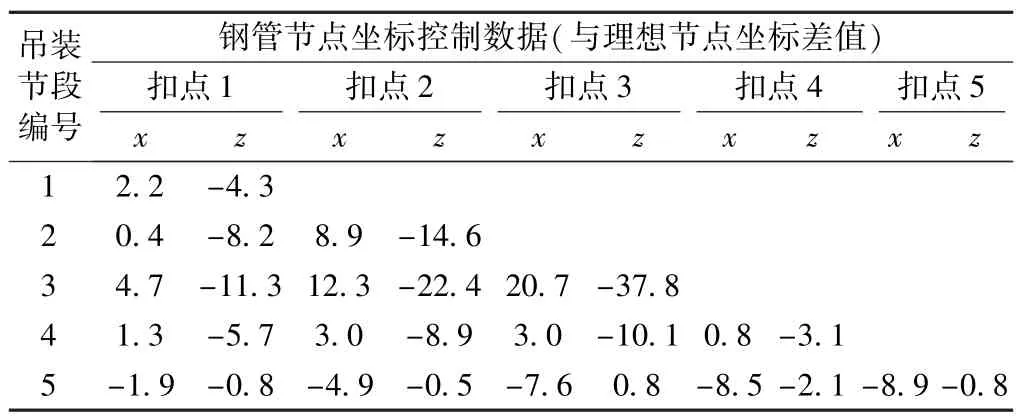
表2 拱肋安装过程中扣点处下弦钢管节点坐标控制数据 mm

3.4 合龙前钢管骨架的温度效应计算

为了有效利用温度效应消除由于扣索锚点较低而导致的骨架纵桥向压缩量,进行了合龙前骨架结构温度效应的理论计算。图5为合龙前骨架结构升温6℃时的结构变形。由图中数据可知,环境温度升高6℃时,骨架纵向位移约为10mm,即利用温度变形很容易抵消骨架的轴向压缩量,保证骨架结构的“零附加应力”合龙。

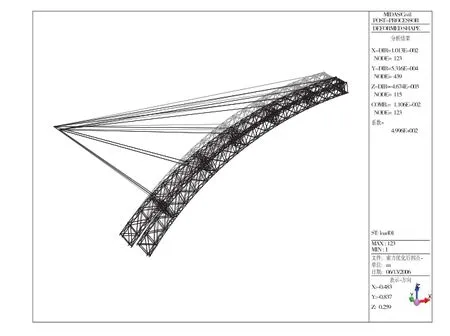
图5 合龙前钢管骨架的温度效应

4 落步溪大桥钢管骨架吊装过程应力测试结果及分析

骨架吊装过程控制采用“线形和扣索索力双控”的原则,其中以表2中的高程数据控制为主,表1中的扣索索力值控制做校核。表3列出了成型的拱肋骨架各截面的实测应力及理论应力。由表3中数据可见,宜昌侧拱脚、1/4截面位置的部分部位弦管总应力与理论总应力相差稍大外,其余各截面的测试部位应力均非常吻合,相对误差均小于10%。表明采用此种吊装控制方法可以准确的保证拱肋骨架的成型质量。

表3 拱肋骨架成型后各测试截面弦管轴向应力实测及理论值 MPa

5 结论

(1)以“有限元零位移法”为基础,采用非线性索单元模拟扣索,将扣索作为整体分析模型的一部分,给出了扣索索力优化的数学模型及迭代计算过程。

(2)针对落布溪大桥拟定的扣索方案,经过非线性迭代计算求得一组最优扣索索力,并进行了骨架节段的正装及倒拆计算,确定骨架合龙前的优化扣索索力,给出了钢管骨架吊装施工中钢管应力及高程的控制数据,为落步溪大桥拱肋骨架的吊装控制提供了控制依据,较好地保证了落步溪大桥的拱肋骨架成型质量。

(3)拱肋骨架的吊装过程应力实测值与理论值比较可知,采用本方法能够保证大跨度钢管拱肋骨架具备良好的“零附加应力”合龙条件,并且在施工中能够给出准确的高程控制数值,避免了繁琐的扣索索力调整工序,保证了吊装过程的一气呵成,具有重要的工程指导意义。

(4)为了更好地保证大跨度拱桥拱肋骨架的“零附加应力”合龙,有必要对合龙前的结构状态进行温度效应的理论计算,以充分利用结构的温度变形消除扣索索力引起的骨架变形,保证骨架的成型质量。

[1] 瞿国钊,刘华全.宜万铁路落步溪大桥178m混凝土拱桥设计[J].铁道标准设计,2005(11):57 -59.

[2] 梅盖伟,张 敏,等.用倒拆修正法计算拱桥施工扣索索力与预抬量[J].重庆交通大学学报,2009(4):199 -202.

[3] 连岳泉,肖建良.大跨径拱桥拱肋吊装过程索力仿真分析[J].中外公路,2008(10):146 -149.

[4] 张建民,郑皆连.大跨度钢管混凝土拱桥吊装过程的优化计算方法[J].桥梁建设,2002(1):52 -58.

[5] HeXiongjun.ShenChewu.Adjustmentofbuckle-cableforcesunder cablehoistingconstructionofconcrete-filledsteeltubulararcbridges. JournalofWuhanTransportationUniversity,1999(10):575 -578.

[6] 马必利.钢管混凝土拱肋的吊装施工控制[J].中外公路,2004 (2):17 -19.

[7] MIDASInc.迈达斯理论手册(第二册),2007(9):9 -13.

[8] 袁海庆,范小春,等.大跨度钢管混凝土拱桥拱肋吊装预测的迭代前进算法[J].中国公路学报,2003(7):48 -51.

[9] 沈成武,杜国东,等.大跨径钢管混凝土拱桥吊装过程中的索力逆分析[J].武汉交通科技大学学报,1998,22(3):223 -226.

U448.22

A

1004 -2954(2010)08 -0178 -04

2010 -05 -17

陈 强(1972—),副研究员,工学博士。