异形独塔双层桥面斜拉桥动力特性及地震反应分析

杨吉新，朱伟伟，丁 兰，李晓亮

(1.武汉理工大学 交通学院，武汉 430063;2.湖北省路路通公路设施工程有限公司，武汉 430053)

随着斜拉桥跨径的不断增大，其结构刚度越来越柔，斜拉桥在动力荷载(如风、地震和车辆荷载等)作用下的动力分析和结构性能倍受工程界关注。而桥梁结构的动力特性包括自振频率、主振型及阻尼等［1-2］，是结构本身固有的，反映桥梁的刚度指标。它对于正确地进行桥梁的抗震设计及维护有着重要的意义。

本文从动力特性的角度出发，对承担双层交通的深圳皇岗—香港落马洲异形独塔双索面斜拉桥进行了动力特性分析，为进一步分析结构的抗震性能和抗风性能打下了基础;同时采用反应谱法分析了结构的线性地震响应，讨论了在两种振型组合方法和三组振型数情况下独塔斜拉桥地震响应的最大值。

1 工程概况

深圳皇岗—香港落马洲大桥为承担双层人行交通的异形独塔双索面斜拉桥，跨径组成为34.20 m+133.65 m+72.15 m，桥面有效净宽16.5 m。主梁底层采用全焊正交异性板桥面钢箱梁，梁高1.7 m，顶板采用厚6 mm的闭口肋，板厚12 mm，底板采用厚6 mm的闭口肋，板厚10 mm，在灌注压重混凝土处加厚至12 mm;中层为正交异性板桥面钢板梁，顶板采用厚6 mm的闭口肋，板厚为12 mm，纵横梁均为 I字梁;顶层为K形栓焊桁架，竖杆与各层之间采用栓接。边跨底层主梁两边灌注混凝土压重，使主跨、边跨竖向重量能大致平衡。索塔基础采用扩大基础，塔在梁底以上高72 m，梁底以下18 m，下塔柱向主跨倾斜 9.8°。两塔柱上下设两道横梁，其下横梁与底层钢梁固结。边跨与主跨索均设13对斜拉索，边跨索距4 m，中跨索距8 m，索梁节点采用钢锚箱结构。设计最大阵风风速62.3 m/s(离地面10 m)，地震基本烈度7度。该桥布置见图1。

本桥的结构具有如下特点;①独塔双索面斜拉桥，主边跨度相差悬殊;②由于双层荷载，活载和二期恒载大于一般的桥梁;③斜拉桥主梁采用不设斜杆的钢框架结构;④塔梁固结，下塔柱向主跨倾斜。该桥由于其独特的结构形式，故需要对其动力特性及抗震性能进行分析。

2 有限元计算模型

2.1 动力特性分析基本方程

Fleming，Egeseli［3］和 Nazmy，Abdel-Chaffar［4］对斜拉桥做过大量的线性和非线性动力分析，认为用线性理论分析得到的结果是可以接受的。

多自由度结构的线性动力有限元控制方程为［5］

式中，M，C，K分别为结构的总质量矩阵、总阻尼矩阵、总刚度矩阵;，x分别为结构加速度向量、速度向量、位移向量。

忽略结构阻尼的影响时，桥梁自由振动的特征方程为

图1 桥梁立面布置(单位:mm)

式中，ω为桥梁系统各阶固有频率，对应着各阶固有振型。

2.2 空间有限元建模原则

为了准确地求解该桥动力特性，建立结构的空间三维模型，对实际结构进行模拟。计算模式的模拟着重于结构的刚度、质量和边界条件的模拟，而且应当尽可能地与实际结构相符。结构的刚度模拟主要指杆件的轴向刚度、弯曲刚度、剪切刚度和扭转刚度，对于一些更复杂的情况，有时也包括翘曲刚度的模拟以及杆件之间的相互刚度，如伸缩装置的模拟等。结构的质量模拟，主要指杆件的平动质量和转动惯量的模拟。边界条件模拟应和结构的支承条件相符。

2.2.1 桥梁构造的模拟

该模型塔柱、墩、承台和主梁边立柱、顶层弦杆均采用空间梁单元模拟，为了准确地模拟堆聚质量分布、振型形状和地震力分布，主塔单元划分相对其它单元更为细密。双层桥面板均采用板单元模拟，斜拉索采用只受拉的桁架单元。由于拉应力和自重垂度影响的非线性刚度特性，采用等效弹性模量的方法，用 Ernst公式进行修正。

2.2.2 质量转化与初拉力的考虑

桥面铺装设计时不做受力计算，即不与主梁构成整体一起承受结构内力，在建模时仅模拟铺装的质量，而不模拟其刚度，按均布荷载加载到桥面单元，然后将荷载转化为质量。在高应力的缆索中，结构的面外刚度在很大程度上受结构缆索的面内应力状态的影响，这种面内应力和横向刚度之间的耦合，称为应力刚化。在有限元数值计算分析中，将拉索索力加到对应的桁架单元，转化为初始刚度矩阵，加到主刚度矩阵上。

2.2.3 有限元模型的建立

根据上述结构各部位的离散，建立斜拉桥结构的空间有限元分析模型如图2。

图2 斜拉桥有限元计算模型

3 结构动力特性分析

在上述斜拉桥计算模型的基础上，采用子空间迭代法计算了桥梁结构的动力特性，表1列出了桥梁结构的前十阶自振频率及相应振型特征。由于篇幅有限，图3、图4给出了前2阶振型图。

表1 结构自振频率及相应振型特征

通过表1及图3、图4可以发现，该异形独塔双层桥面斜拉桥动力特性的特点为:

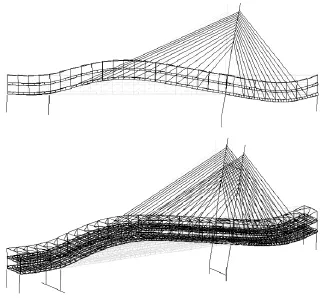
图3 第1阶振型

图4 第2阶振型

1)本桥第一振型为主跨和右边跨反对称竖弯，塔纵弯，基本周期为1.337 4 s，与其它大跨度斜拉桥的周期相比［6］，周期比较短，主要原因是由于该桥跨度不大，且塔梁固结，刚度比较大，这对减小结构的地震位移是有利的，但将产生较大的塔底内力。

2)斜拉桥的自振特性表现出明显的三维性和相互耦合的特点。该桥采用的是双索面，提高了结构的抗扭刚度，但随着频率的提高，斜拉桥结构扭转频率所占比重较大，且结构振型表现为弯扭耦合，对该桥的抗风稳定性不利。因此，在进行风振分析时，应注意高阶振型的影响。

3)斜拉桥具有密布的频谱。斜拉索具有膜的性质，大跨度斜拉桥的模态比一般的结构密集得多，在一个较宽的频率范围内，许多振型都可能被动力荷载激起强烈的振动，所以对大跨度斜拉桥一般采用10阶以上的振型进行分析。

4 地震反应分析

反应谱方法是目前结构抗震设计中广泛使用的方法。其优点是只取少数几个低频振型就可以求得较满意的结果，计算量少;再者，反应谱法能将时变动力问题转化为拟静力问题，易为工程师所接受，可以指导抗震初步设计。在反应谱分析中，设计反应谱的合理选择是很重要的，为安全起见，选取我国现行的《公路工程抗震设计规范》中给出的规范反应谱。

对于复杂的大型空间结构，在地震动的有效频率范围内可能密集地分布着数以百阶计的自振频率。故而，对振型个数的选取是首先应该考虑的，一般建议至少取前50阶振型(当选择的频率阶数不足时会使某些截面的反应值失真，导致不安全的结果)。为便于分析比较，本文分别选取了50阶、70阶和90阶振型。目前，应用广泛的是基于随机振动理论所提出的2种组合方法，即 SRSS法和 CQC法［7］。其中，SRSS法的最大位移响应表达式为

SRSS法在许多桥梁地震响应计算中得到了广泛的应用，但是，对于几何形状特殊、振型不连续的桥梁不能按SRSS法计算地震响应，当结构的自振频率非常接近时，用SRSS法计算得到的结果误差比较大，这时采用完全平方组合法，即 CQC法比较合理。与SRSS法相比，CQC法增加了考虑不同振型之间相互影响的相关系数，即

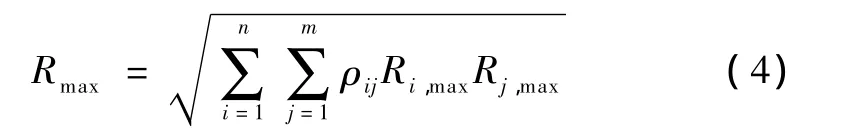
式中，ρij为振型相关系数

如果两个自振频率相差较大，振型相关系数就会减小，特别是当

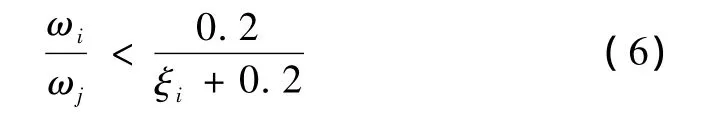
时，可以认为振型相关系数近似为0，则 SRSS法和CQC法相同。

该异形独塔双层桥面斜拉桥的场地条件是Ⅰ类，场区地震基本烈度7度。输入加速度峰值为0.1 g时的加速度反应谱，计算各振型的最大位移响应和相应构件的地震内力，再由各振型组合公式，求出结构反应量最大值的一个近似估计值。沿纵桥向和横桥向地震作用的计算结果见表2。

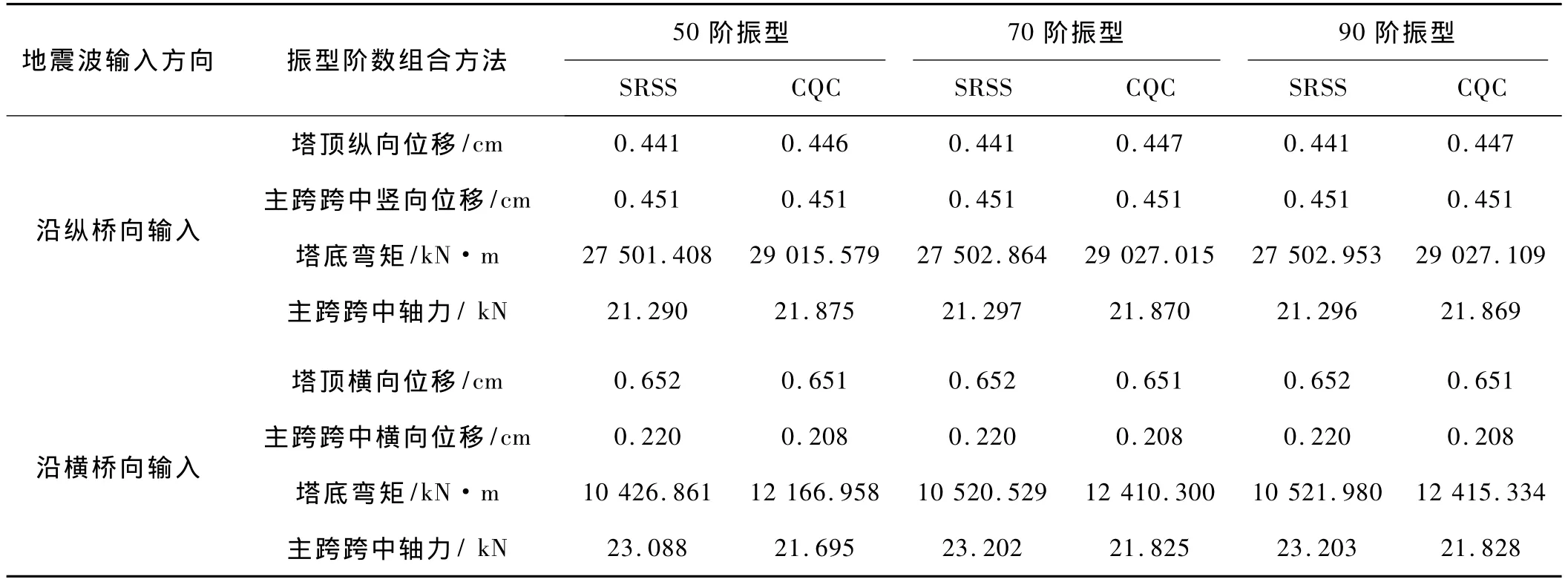
表2 结构地震反应最大值

由表2可知，采用50，70，90阶振型，对结构的地震响应影响不大，取前50阶振型基本包括了对结构响应贡献较大的振型，且采用 SRSS和CQC这两种组合方法的计算结果较为接近，满足工程抗震设计的需要。

5 结语

本文采用大型有限元分析程序对深圳皇岗—香港落马洲异形独塔双层桥面斜拉桥的动力特性及线性地震反应进行了分析，对其抗震性能有了一定的了解，得到了如下的结论:

1)该异形独塔斜拉桥的基本周期为1.337 4 s，不属于长周期结构，这主要原因是由于该桥跨度不大，且塔梁固结，刚度比较大。

2)采用反应谱分析法中的两种振型组合法(SRSS法和CQC法)均能较好地分析结构的线性地震反应，计算结果较为接近，都可以用于该桥的抗震分析计算。

［1］李国豪.桥梁结构稳定与振动［M］.北京:中国铁道出版社1992.

［2］李国豪.工程结构抗震动力学［M］.北京:中国铁道出版社，1980.

［3］FLEMING J F，EGESELI E A.Dynamic Behavior of a Cable-Stayed Bridge［J］.Earthquake Engineering ＆ Structural Dynamics，1982，8(1):1-16.

［4］NAZMY A S， ABEDEL-CHAFFAR A M.Non-linear Earthquake Response Analysis of Long-Span Cable-Stayed Bridges:Theory［J］.Earthquake Engineering ＆ Structural Dynamics，1990，19(11):45-62.

［5］户川隼人.振动分析的有限元法［M］.殷荫龙，陈学源译.北京:地震出版社，1985.

［6］范立础.桥梁抗震［M］.上海:同济大学出版社，1997.

［7］SINHA R，LGUSA T.CQC andSRSSmethodsfornonclassically damped structures［J］.Earthquake Engineering ＆Structural Dynamics，1995，24(6):615-619.