基于神经网络的沥青路面基层裂缝应力强度因子预测模型
王宏畅,李国芬,王元纲
(1.道路结构与材料交通行业重点实验室 (长沙理工大学),长沙 410004;2.南京林业大学,南京 210037)
高等级路面结构出现裂缝导致早期破坏已是一个普遍性的问题,路面裂缝尖端应力强度因子是判断裂缝扩展的一个重要指标[1]。为了掌握裂缝开裂和扩展规律,确定道路的剩余使用寿命,以便为设计各种防裂措施提供必要的理论依据,近年来许多学者基于断裂力学和有限元理论对路面体进行解析或数值分析,计算裂缝的应力强度因子,但是应力强度因子的计算是很复杂的,决定应力强度因子的参数很多,主要有材料参数、结构参数、裂缝尺寸、荷载形式、位置参数等,采用有限元法计算上述设计变量时,有限元网格需要重新划分,计算在操作上将很困难。尤其对裂缝进行计算时,为正确反映其裂缝尖端的奇异性,尚需在裂缝尖端构建复杂的特殊单元,因此计算的时间将要以日、月甚至年来计量。这也是基于断裂力学路面结构设计方法近期发展缓慢的原因之一,为解决这一问题,并考虑到目前高等级沥青路面多采用模量较高的半刚性基层,基层将先于面层产生疲劳开裂,本文采用人工神经网络的方法,利用人工神经网络具有较强的记忆能力和预测能力,建立了沥青路面基层裂缝应力强度因子的预测模型。
1 人工神经网络
人工神经网络是一种具有大量连接的并行分布式处理器,它具有通过学习获取知识并解决问题的能力。而神经网络的自学习、自组织和信息处理的并行性正是将神经网络技术应用于带裂纹路面结构应力强度因子计算的关键。
与传统方法相比,神经网络法具有多种有吸引力的特征和优势:
(1)非线性特性。理论上,神经网络能以任意精度实现任意非线性映射,网络还可以实现较其它方法更优越的系统建模。这种特性使我们有可能建立在路面厚度、模量及裂缝尺寸等多因素影响下的计算。
(2)多变量系统。神经网络可以处理很多输入信号,针对带裂纹路面结构,可以输入如路面材料、尺寸、裂纹类型、裂纹尺寸、荷载、温度等参数,从而在应力强度因子与实际工况之间建立更广泛的联系。
(3)学习和自适应能力。神经网络是基于所研究系统过去的数据记录来进行训练的。当提供给网络的输入不包含在训练集中时,一个适当的训练了的神经网络具有归纳能力[2]。
到目前为止,人们从不同角度构筑了近百种神经网络模型,这些模型的结构、概念、学习算法和工作方式各不相同。根据结构,神经网络可以分为前馈网络 (Feedforward Network)和反馈网络(Feedback Network)。目前,反向传播神经网络模型 (Black Propagation,简称BP模型)是应用较广泛的一种,这也是本文所采用的模型。
2 应力强度因子计算
采用断裂力学理论,应用通用有限元软件ABAQUS计算半刚性基层底裂缝应力强度因子值。由于常规有限元在靠近裂尖处难以正确反映裂缝尖端应力场的奇异性,故在裂缝尖端需设置奇异单元。三维裂缝尖端的奇异单元采用20结点的6面体所退化的五面体单元 (如图1所示),退化面化为裂缝前缘,并将中间结点移置于靠近裂缝尖端四分之一边长时,其满足裂缝尖端的r-1/2奇异性[3]。裂缝尖端的局部坐标系如图2所示,根据线弹性断裂力学理论,裂缝尖端附近位移场的表达式如 (1) ~ (3)[4]。
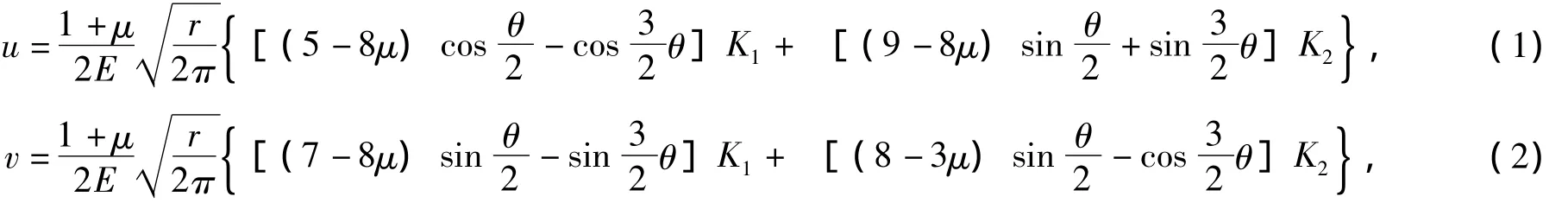
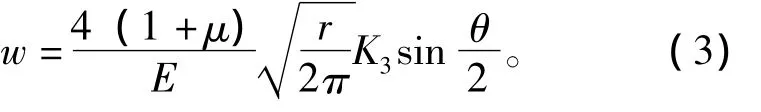
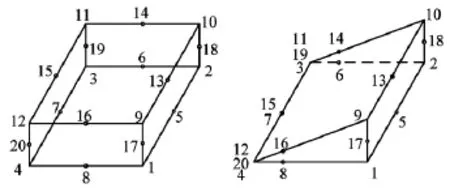
图1 常规单元与奇异单元Fig.1 Conventional unit and singular unit
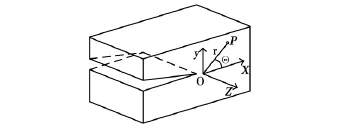
图2 三维裂缝尖端坐标系Fig.2 Three-dimensional crack tip coordinate system
式中:E为材料弹性模量;μ为材料泊松比;K1、K2、K3分别对应为张拉型、剪切型、撕裂型裂缝的应力强度因子。利用有限元法计算裂缝尖端的应力强度因子,多采用位移法,在求得裂尖附近的位移场后,进而可以由上式推得裂纹尖端的应力强度因子。
路面结构各组成部分的材料具体特性及厚度参数见表1,对不同裂缝尺寸,各层材料及厚度取交叉组合,分别进行有限元计算。计算荷载采用标准双轮轴载100 kN,胎压0.707 MPa。轮胎接触面积由一个矩形和两个半圆形组成[5](如图3所示)。
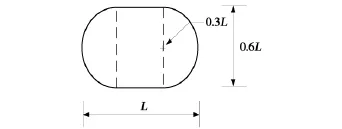
图3 轮胎与路面实际接触面积Fig.3 The actual contract area between tire and road surface

表1 路基及路面结构计算参数Tab.1 Calculation parameters of subgrade and pavement structure
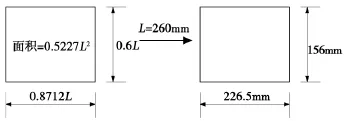
图4 轮胎与路面当量接触面积Fig.4 Contract area between tire and road equivalent
为方便有限元计算,接触面积可进一步简化为等宽的单一矩形0.8712 L×0.6 L(如图4所示),其中L=260 mm。并考虑两种最不利荷载位置如图5所示[6-11]。其中图5(a)为正荷载,图 5(b)为偏荷载,计算模型如图6所示。
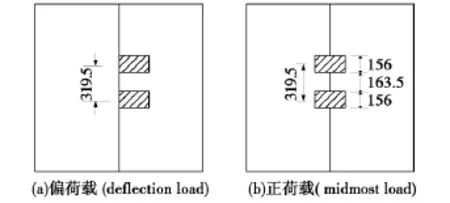
图5 荷载位置 (mm)Fig.5 Load location(mm)
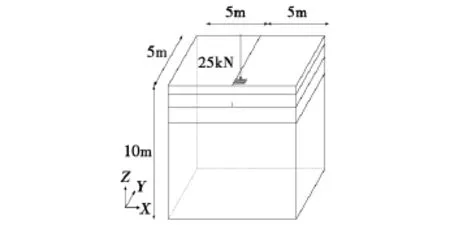
图6 计算模型Fig.6 Calculation model
3 应力强度因子预测模型
3.1 建立神经网络的步骤
影响基层底裂缝应力强度因子的主要因素有:荷载、裂缝长度、基层模量及厚度、面层模量及厚度和底基层模量等,应力强度因子可以用这几个影响因素的非线性函数来描述如公式 (4)。
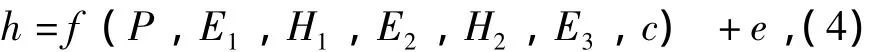
式中:P为荷载因素;f为未知的非线性映射函数;E1、H1为面层的模量和厚度;E2、H2为基层的模量和厚度;E3为底基层模量;c为裂缝长度;e为非线性映射函数的误差。
根据上述关系建立预测基层裂缝应力强度因子的BP网络模型。①将荷载位置、裂缝长度、基层模量和厚度、面层模量和厚度和底基层模量作为BP网络的输入向量;②对应的应力强度因子K1和K2作为网络输出向量;③用学习样本训练神经网络,确定各层的权重和阈值;④对于训练好的BP网络模型,用检验样本进行网络检验,判断网络的适用性及其精度。
3.2 BP网络的设计
按照BP网络的设计方法[12],同时考虑到本文所需解决的实际问题,输入层的神经元数为7个。为了简化模型和便于调整网络,设置一层隐含层,其神经元的数目略微大于输入层的神经元数目。输出层的神经元数目与目标类型的个数一致,即2个神经元,代表基层裂缝的应力强度因子K1和K2。预测基层裂缝的应力强度因子的BP网络结构如图7所示,其中隐含层的神经元数目可以根据计算结果调整。学习率均为0.01,目标误差为0.0 000 001,最大循环次数为1000次。基于误差反向传播算法的多层前向神经网络 (BP网络),采用sigmoid型可微函数作为传递函数,可以实现输入和输出间的任意非线性映射,广泛地应用于函数逼近、模式识别、数据压缩等领域,隐层单元的传递函数为正切sigmoid函数,输出层采用纯线性传递函数pureline函数[13]。如图7所示。
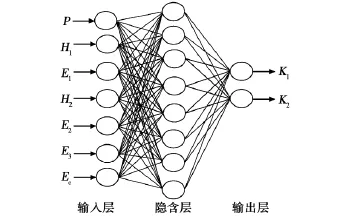
图7 三层BP网络结构Fig.7 Three-layer BP network structure
3.3 BP网络模型的训练
以ABAQUS计算半刚性基层底裂缝应力强度因子值作为训练样本,在BP网络输入中分别以0和1来代表正荷载和偏荷载,总共有874组数据,随机选取54组数据作为检验样本,其余作为学习样本,对BP网络进行训练和检验[14]。通过改变隐含层的神经元数目,建立预测基层裂缝的应力强度因子的BP网络模型,经过训练比较,确定隐含层的神经元数目为14个。网络模型训练后,其训练的目标误差变化过程如图8所示。
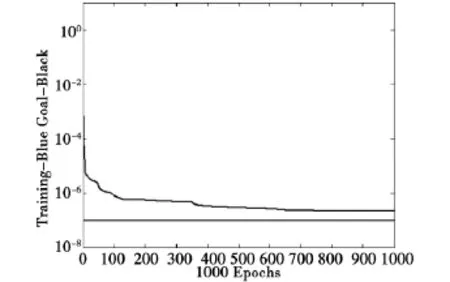
图8 BP网络训练中的目标误差变化Fig.8 Target error changes in BP network training
从训练误差曲线看到,神经网络的训练误差收敛很快。另外需请注意在网络训练之前必须对样本数据进行归一化处理,并在训练过程中采用贝叶斯正则化方法以保证神经网络的推广能力。
3.4 BP网络模型的检验
为了检验BP网络模型对基层裂缝的应力强度因子预测的可行性,用随机抽出的54组数据作为检验样本,检验了BP网络预测模型(见表2)。因篇幅所限,表中只列出了部分数据。
经过多次训练,对于测试样本,BP网络模型模拟的基层裂缝的应力强度因子与实测值的最大相对误差为4.5%,相对误差绝对值的平均值为0.9%。预测值与实测值的相关程度很高,表明通过该BP网络模型预测的基层裂缝的应力强度因子是可信的,完全满足使用要求。因此,该网络具有很强的泛化能力,在实际运用中,能够方便快捷地得到应力强度因子。
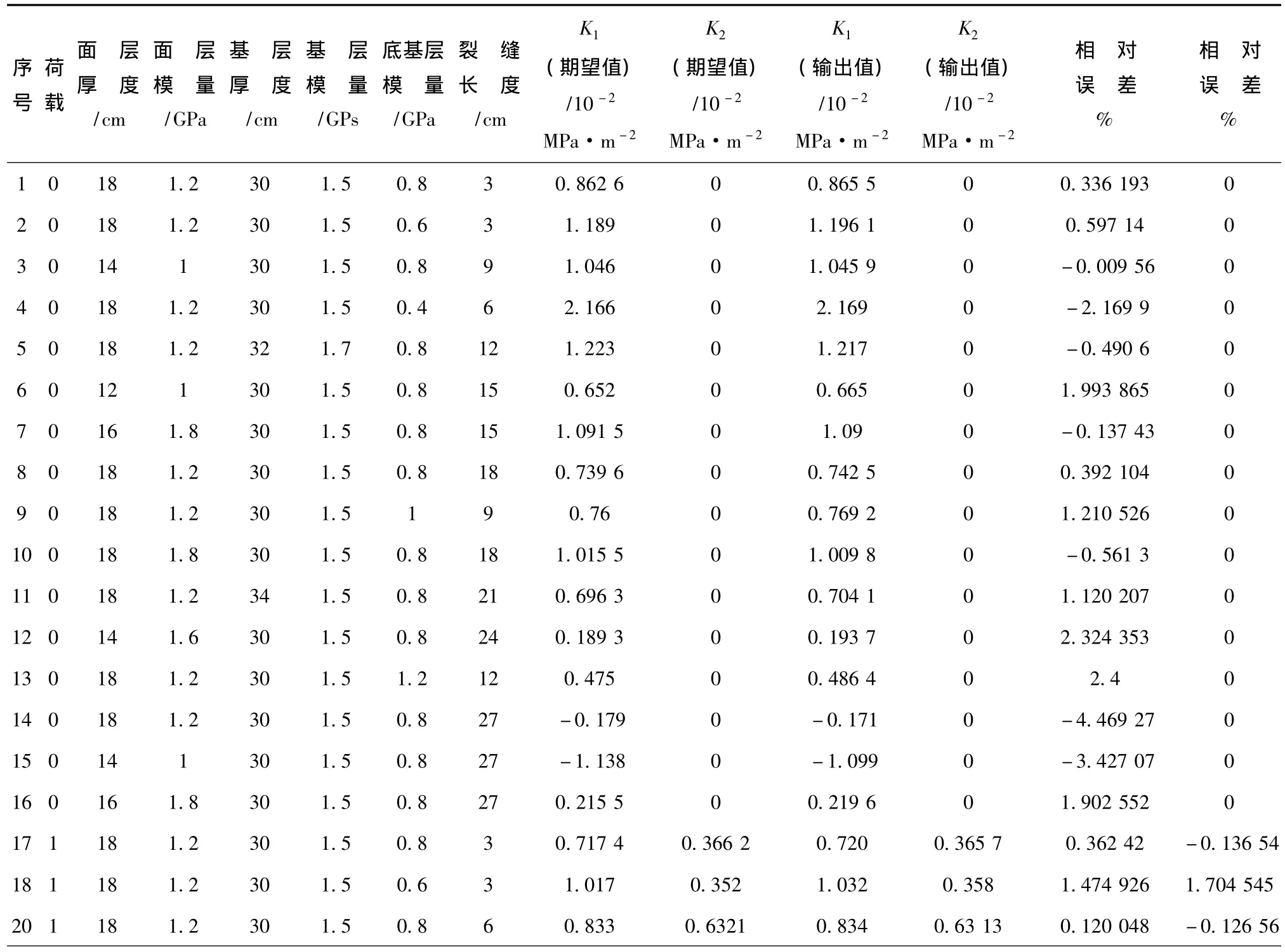
表2 检验样本与预测误差Tab.2 Test samples and prediction errors
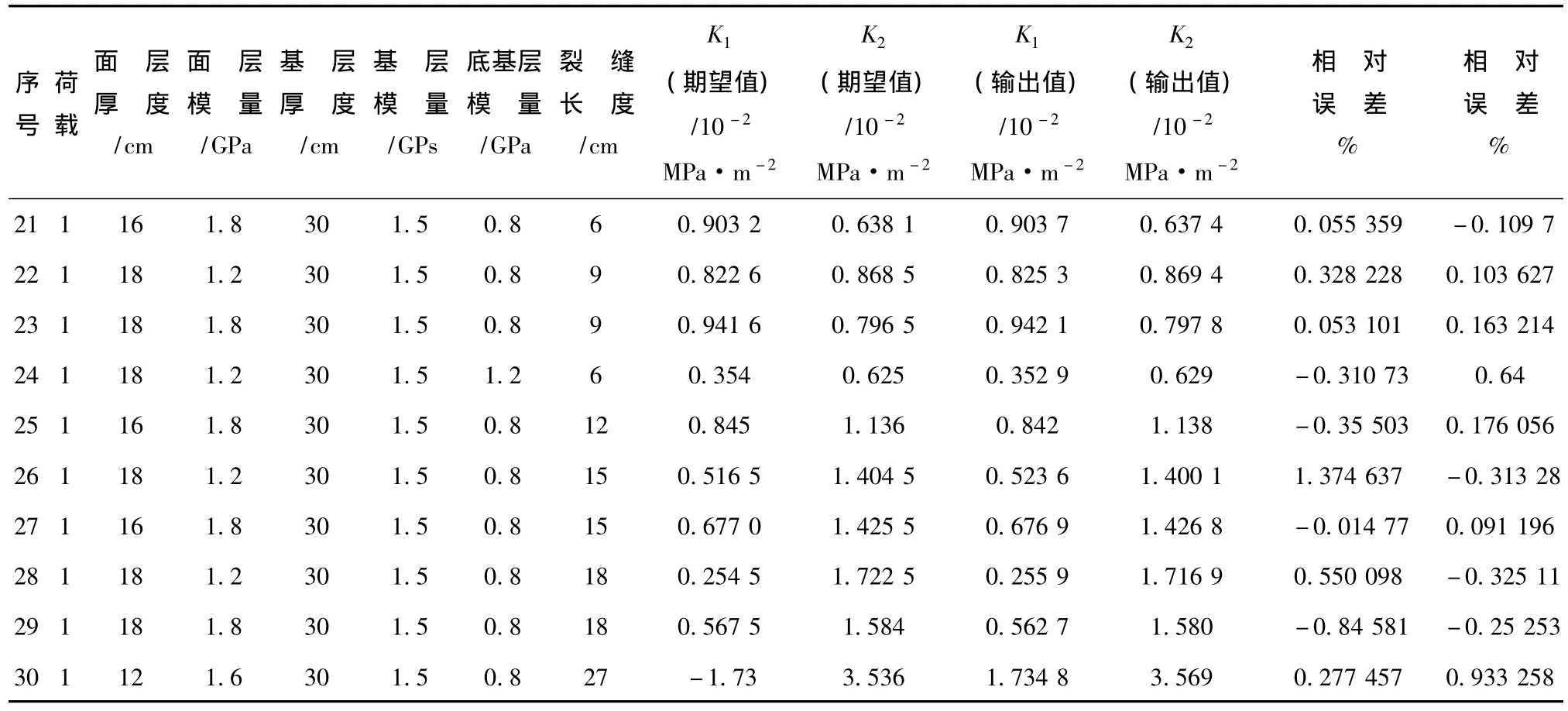
续表2 检验样本与预测误差Tab.2 Test samples and prediction errors
4 结论
基于断裂力学及有限元理论,应用有限元程序ABAQUS,建立三维有限元模型,简化行车荷载模式,计算半刚性基层沥青路面基层反射裂缝不同裂缝长度时的应力强度因子。并采用神经网络理论,建立起沥青路面基层反射裂缝的应力强度因子神经网络预测模型,通过大量的计算、验证与比较,训练好的BP网络计算应力强度因子具有很高的精度,使用BP网络可取代传统计算方法中的有限元分析。给经过训练的BP网络依次输入面层厚度和模量、基层厚度和模量、底基层厚度和模量、土基模量以及裂缝长度,BP网络计算出一个输出,与有限元分析相比,使用BP网络进行分析的速度要快几个数量级,因而大大加快了结构设计过程中结构分析的速度,从而加快了整个结构设计的进程。
[1]郑健龙,周志刚,张起森.沥青路面抗裂设计理论与 [M].北京:人民交通出版社,2002.
[2]徐秉铮,张百灵,韦 岗.神经网络原理及应用 [M].广州:华南理工大学出版社,1994.
[3] Castell M A,Ingraffea A R,Irwin L H.Fatigue Crack Growth in Pavements [J].Journal of Transportation Engineering,ASCE,2000,126(4):283-290.
[4]沈成康.断裂力学[M].上海:同济大学出版社,1996.
[5]黄仰贤.路面分析与设计[M].北京:人民交通出版社,1998.
[6]王宏畅,李国芬,黄晓明.高等级沥青路面表面裂缝扩展规律及寿命研究[J].公路交通科技,2007,24(7):10-14.
[7]王宏畅,黄晓明.高等级沥青路面基层底裂缝三维数值分析[J].公路交通科技,2005,22(12):1-4.
[8]郑健龙,张起森.半刚性路面反射裂缝及其应力强度因子的有限元分析[J].岩土工程学报,1990,12(3):22-31.
[9]王宏畅,黄晓明,傅 智.半刚性基层表面裂缝影响因素[J].交通运输工程学报,2005,5(2):38-41.
[10]王宏畅,李国芬,侯曙光,等.高等级沥青路面基层底裂缝扩展规律 [J].南京林业大学学报 (自然科学版).2007,3(31):78-82.
[11]杨 林,杨 磊,陈 晗.季冻区沥青路面早期病害成因及防治[J].森林工程,2008,24(3):63-65.
[12]闻 新,周 露,王力丹,等.Matlab神经网络应用设计[M].北京:科学出版社,2000.
[13]宋云连,张永强,季羽中鹏.沥青路面显式功能函数的推导及其可靠度分析[J].公路工程,2009,34(1):1-4.
[14]付凯敏,陶海峰.半正弦荷载下沥青混合料变形特性力学模型研究 [J].公路工程,2009,34(1):136-138.

