小波分析与Hilbert变换在25T型客车故障诊断中的应用

孙惠琴,钟 原

(中国铁道科学研究院 机车车辆研究所,北京100081)

随着我国客车的不断提速,对客车的安全监测要求也不断提升。需要在运行中及时诊断和发现故障,以便保证客车的运行安全。

25T型客车是在25K型客车基础上进一步提升技术性能和设施功能的铁路新型客车,其持续运行速度为160 km/h。25T型客车配套的转向架为CW-200K型和SW-220K型等。在客车运行过程中,转向架和轮对逐渐出现了不少故障,包括转向架失稳;空气弹簧破裂;轮对擦伤、剥离、动不平衡等。这些故障使得客车振动异常,降低了旅客乘坐的舒适度,造成安全隐患,特别是转向架垂向振动尤为突出,严重地影响了行车安全,必须及时准确地诊断出这些故障,以保证客车的安全。

在25T型客车的运行过程中,为了保证行车安全,需要及时进行故障诊断,报告各个车厢中转向架的状态,包括轮对是否有故障(擦伤、剥离、动不平衡等)、构架的稳定性、空气弹簧的运行状态等,以便提醒客车上的工作人员及时进行处理,避免发生事故。

小波分析与Hilbert变换在信号处理中的应用越来越广泛。小波分析是一种较好的时频分析技术,在信号的去噪、消除奇异点、故障诊断等方面表现出了良好的性能;Hilbert变换可以分析信号的包络。本文采用了小波分析与Hilbert结合方法,对实际采集的25T型客车正常数据和轮对擦伤数据、动不平衡数据进行了分析。因为采集的数据中包括有噪声数据,通过小波分析,可以滤去噪声;通过Hilbert变换,可以提取出数据的包络。详细阐述了小波分析与Hilbert变换在25T型客车故障诊断中的应用过程与结论。

1 小波分析技术

小波变换是一种积分变换。它具有多分辨特性,可以按照不同的尺度将信号进行分解,实现了将复杂信号分解成一些简单信号,从而在不同的频带对信号进行精细观察和分析。

基本小波ψ(t)经过伸缩和平移后的小波函数族为

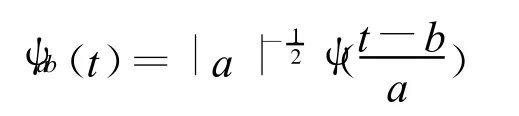
其中a为尺度因子,b为平移因子。

设 f(t)为一信号,其小波变换的定义为 f(t)与小波函数族 ψab(t)的内积,即:

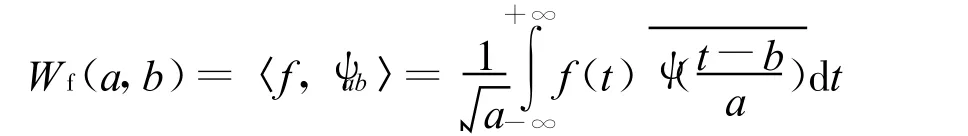
其重构公式(逆变换)为:

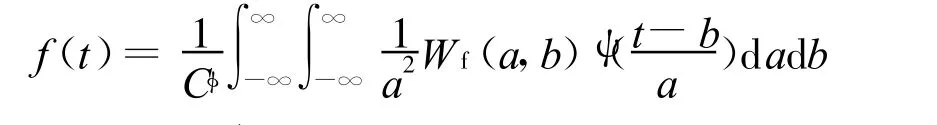
直接按照上述公式计算小波变换和重构,计算量很大。在小波分析的发展历史上,先后经历过基础理论发展阶段和实用阶段,Mallat提出的快速算法将小波推向了实用。其著名的分解算法如下:

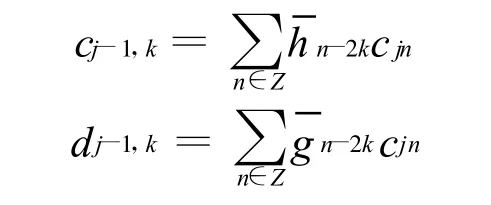
Mallat重构算法为:

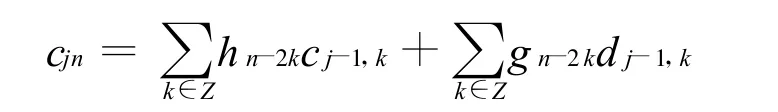
由Mallat算法可以知道,信号经过1,2,…,j的多尺度分解,最后分解为尺度系数c1,c2,…,cj和小波系数d1,d2,…,dj,包含了振动信号由高频到低频各个不同频带的频率信息,是振动信号的多尺度分解后的时频表示。其中,尺度系数cj代表了振动信号的低频近似成分,而小波系数dj代表了振动信号的高频细节成分。由于小波分析的多分辨特性,其具有良好的时频分析性能,从而为25T型客车转向架和轮对故障诊断提供了有效的分析手段。

2 Hilbert变换

通过对信号的Hilbert变换,可以获得信号的包络。

Hilbert变换公式为:

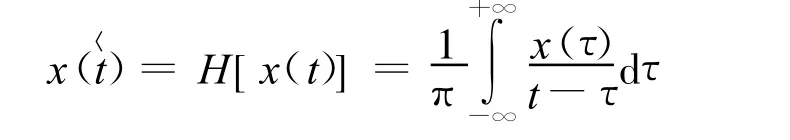
构造其解析函数

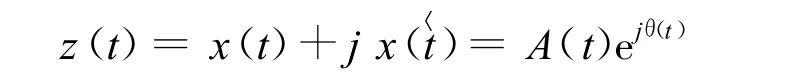
利用Hilbert变换进行信号包络的原理是让原信号产生一个90°的相移,与原信号一起构成解析信号,取模后形成包络。

3 小波分析和Hilbert变换进行25T型客车的故障诊断过程

以25T型客车运行过程中的正常信号和轮对擦伤信号、轮对动不平衡信号为基础,使用小波分析和Hilbert变换相结合的方法进行故障诊断。整个过程包括数据采集和数据处理两部分。

首先要进行25T型客车的数据采集,采集正常信号和轮对擦伤故障信号、轮对动不平衡信号,方便以后的对比分析;

其次,要对采集的数据进行处理,处理过程主要包括:采用了紧支集正交小波Daubechies小波DB10,对原始信号进行了3层小波分解;并对分解后的小波系数分析,对小波系数求Hilbert包络及其功率谱、功率谱标准差,分析正常信号和故障信号的包络、功率谱和功率谱标准差之间的不同之处;使用能量分析,分析正常信号和故障信号小波分解后各层的能量,建立正常数据和故障数据的能量分布数据库,以便统计、分析、判断正常信号和故障信号。

3.1 数据采集

轮对的擦伤和动不平衡会引起转向架的垂向振动增加,因此,传感器需要被安装在构架上,采集的信号为构架垂向加速度信号。采样频率为512 Hz。要求构架传感器的测量范围满足-10.0～10.0g之间。

3.2 对采集数据的处理过程

使用Matlab语言,对采集的正常信号和轮对擦伤信号、轮对动不平衡信号进行对比分析处理。首先进行小波分解;然后对小波系数进行Hilbert变换,并计算功率谱,比较这3种信号的不同之处;最后计算这3种信号小波分解后不同的能量分布。

(1)原始信号

图1中,从原始信号无法分辨出正常信号、轮对擦伤信号以及轮对动不平衡信号。下面将对3种信号进行小波分解,对比分解后的不同之处。

(2)小波分解后的信号

图2是轮对擦伤信号、轮对动不平衡信号和正常信号的小波分解高频细节系数d1～d3和低频近似系数。

其中,高频细节系数d1～d3代表了原始信号的高频细节。d1层高频细节信号包含了较多的噪声,因此,小波分解可以起到过滤噪声的作用。故障信号的d2层、d3层信号分布不均匀,幅值大小不均匀。而正常信号的d2、d3信号分布都比较均匀,幅值大小也比较均匀。

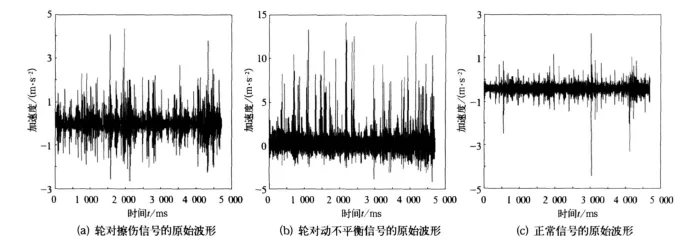
图1 原始振动信号波形

图2 小波分解后 d1～d3和a1～a3信号

低频近似系数a1～a3代表了原始信号的近似信号,可以看出,正常信号的小波近似系数a1、a2分布比较均匀,幅值大小比较均匀,只是偶而会有一次冲击,主要是由于线路的局部不平顺、三角坑等引起的;而轮对擦伤信号和动不平衡信号的小波近似系数a1、a2则包含了明显的周期性故障冲击信号,主要是由于轮对故障引起的,如果轮对有擦伤和动不平衡,则轮对每转动一周,就会对转向架产生一次较大的故障冲击,由此而产生了周期性故障冲击信号。

(3)Hilbert变换

由小波分析理论可知,原始信号可以分解为 d1、d2、a2层信号,而 a2层信号又可以分解为a3层和d3层信号。细节d1信号包含了较多的高频噪声信号,小波分解相当于对噪声进行了过滤,得到的近似信号a2包含了故障信息,分析a2层信号,可以进行故障诊断。对a2层信号进行Hilbert变换,得到Hilbert包络,进而进行功率谱分析,得到图3的功率谱图。由图3可以看出,轮对擦伤与动不平衡信号在10 Hz左右及其倍频附近的故障冲击远远大于正常信号的冲击;轮对擦伤与动不平衡信号在10 Hz附近的能量远远大于其他频段的能量,而正常信号在各个频段的能量分布比较均匀。

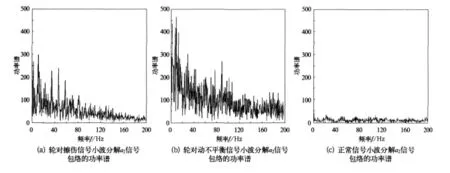
图3 小波分解后a2信号包络的功率谱

25T型客车的运行速度大多在100～160 km/h左右,最高速度可以达到200 km/h,而其轮对的直径一般为915 mm,轮对运行频率与运行速度的关系可以由下面的公式进行计算,其中v为客车的运行速度,D为客车的轮对直径,n为轮对的旋转频率:

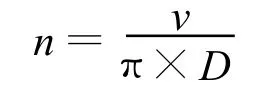
当运行速度为100 km/h时,计算的轮对旋转频率为:

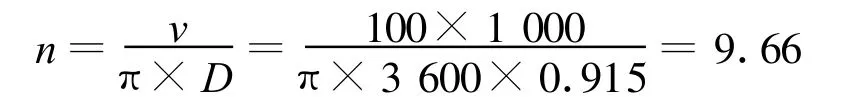
当运行速度为160 km/h时,计算的频率为:

当运行速度为200 km/h,计算的频率为:

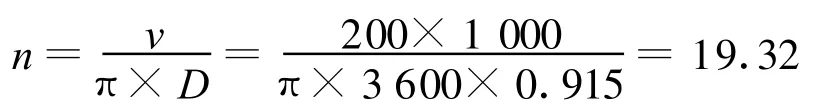
图3的功率谱图中,轮对擦伤与动不平衡信号在10～20 Hz及其倍频的功率谱较大,这是因为当轮对出现擦伤与动不平衡故障时,每旋转一周,就会对构架产生一次较大的故障冲击,即故障冲击的频率为 10～20 Hz;而正常信号在各个频段的冲击能量分布比较均匀。所以,通过小波分析和Hilbert变换,可以找到正常信号和轮对擦伤信号、轮对动不平衡信号的不同之处。

统计量中,标准差表示了随机变量 x的取值与其均值的偏离程度,其公式为:

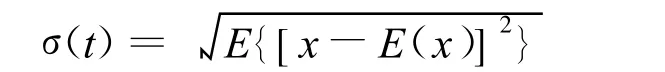
其中E(x)为随机变量x的数学期望。

标准差越小,x取值越集中在其均值附近;标准差越大,x取值越分散。可以用此特征量来表征图3的功率谱,因为正常信号的能量分布比较均匀,所以,其标准差应该比较小;而轮对擦伤与动不平衡信号在10 Hz附近的能量远远大于其他频段的能量,即分布不均匀,其标准差应该比较大。计算结果如表1所示。轮对擦伤与动不平衡信号的标准差远远大于正常信号的标准差,轮对擦伤信号的标准差是正常信号标准差的7倍左右,而轮对动不平衡信号的标准差是正常信号标准差的十几倍。试验结果与理论分析一致。

表1 功率谱的标准差表

(4)能量分布的不同

计算小波分解后各层信号的能量分布如表2,代表了小波分解后各层信号的能量分布比例,即各层信号的能量与总能量的比值。可以看出,正常信号和轮对擦伤信号、轮对动不平衡信号在d3层和a3层信号的能量分布有明显的不同,因为a2层信号可以分解为a3层和d3层信号,所以正常信号和轮对擦伤信号、轮对动不平衡信号在a2层的能量分布也有明显的不同,这也验证了上节中正常信号和故障信号的a2层的Hilbert包络功率谱明显不同的结论。

通过不断收集25T型客车运行过程中故障数据和正常数据,以及其小波分解后包络的功率谱、功率谱标准差和能量信息,建立相应的数据库,找到规律,以便准确地定位故障。

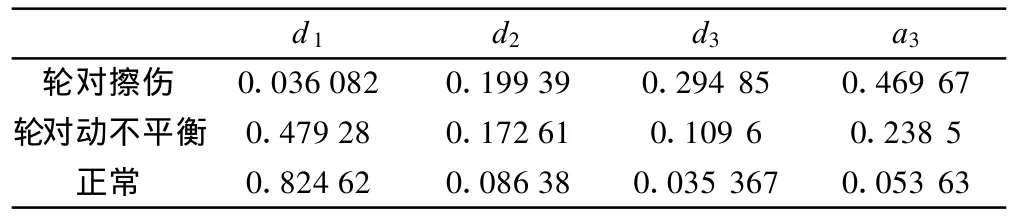
表2 能量分布表

4 结束语

25T型客车振动信号属于非平稳时域变化信号,时频分析方法是处理非平稳时域变化信号的有用工具,在故障诊断方面的优势日渐明显。本文使用了时频分析方法的小波分析和Hilbert变换技术,对25T型客车的轮对擦伤和动不平衡故障进行了诊断,试验结果显示了本方法的有效性。时频分析技术在车载故障诊断系统中具有广阔的应用前景。

[1] 严隽耄.车辆工程[M].北京:中国铁道出版社,2004.

[2] 周 伟.M ATLAB小波分析高级技术[M].西安:西安电子科技大学出版社,2006.

[3] 张 辉,王淑娟,等.基于小波包变换的滚动轴承故障诊断方法的研究[J].振动与冲击,2004,23(4):127-130.

[4] 高国华,等.小波包——包络分析在滚动轴承故障诊断中的应用[J].煤矿机械,2005,(3):127-129.

[5] 王江萍,等.基于小波多分辨分析的往复机械故障特征提取与识别[J].西安石油学院学报,1998,(1):30-52.

[6] 杨国安,等.机械故障信号小波包分解的时域特征提取方法研究[J].振动与冲击,2001,20(2):25-28.

[7] 李顺酩,等.微弱振动信号的谐波小波频域提取[J].西安交通大学学报,2004,(1):51-55.