轨道车辆用空气弹簧阻尼特性研究与应用

莫荣利,陈灿辉,陈文海,邹 宇,郭红锋

(株洲时代新材料科技股份有限公司,湖南株洲412007)

随着轨道交通运输安全性、舒适性和高速化要求越来越高,车辆及其转向架功能集成化和轻量化设计成为当今的发展趋势。带有节流装置的空气弹簧不仅是车辆悬挂系统中的弹性支撑元件,而且是悬挂系统中的减振阻尼元件,是功能集成化和轻量化设计的典型应用。

空气弹簧的阻尼作用是通过安装在空气弹簧本体与附加空气室之间的节流孔(阀)来实现的,如图1所示。当空气弹簧变形时,两者之间将产生压力差。空气弹簧在静态变形(或缓慢变形)过程,其压力差不大,但在振动过程,其压力差较大。空气通过节流孔时由于流程阻力而吸收振动能量,从而实现衰减振动的作用。

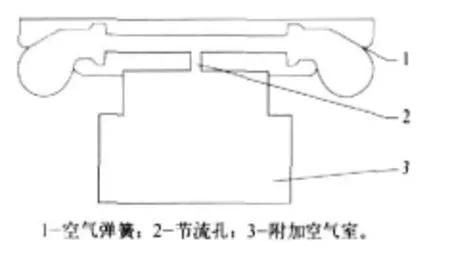
图1 有阻尼空气弹簧结构示意图

1 空气弹簧阻尼的基础理论

1.1 空气弹簧的力学模型

根据理想气体状态方程,在标准状态下,空气弹簧和附加空气室的多变过程可以用以下方程式描述:

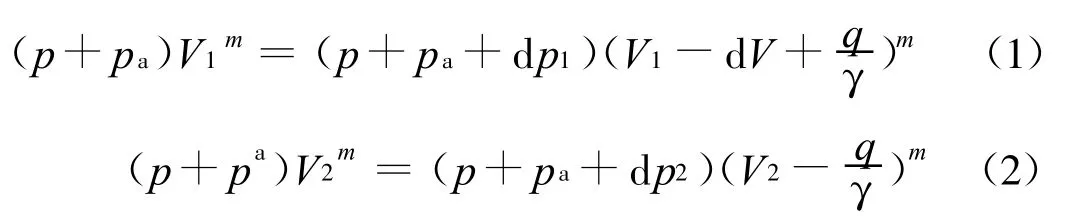
对于微小变形,将上式展开成级数,并略去二阶以上的微小量后整理可得:

当空气弹簧有效面积A在其变形x的变化率dA/dx不大的情况下,空气弹簧容积变化量dV可以近似表示为:

自标准状态变形后,空气弹簧上产生的作用力Px为:

又根据流体力学理论,节流孔的流量特性近似表示为:

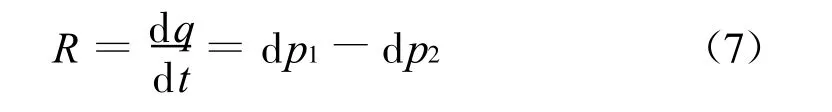
由式(3)～(7)消去q,dp和dV则有

令 y=(A/kP1′)dp2,则式(8)改写为:

式中

式(9)关系可以用图2所示的力学模型表示,图中的各参数与式(10)的各参数相对应。所以节流孔起作用的空气弹簧,相当于一个弹性支撑的减振器系统,即内容积为V2、有效面积为A的空气弹簧和阻尼系统为c1=Rγ A2的减振器并联,而它又和内容积为V1,有效面积为A的空气弹簧串联后,再与有效面积变化率有关的弹簧并联。

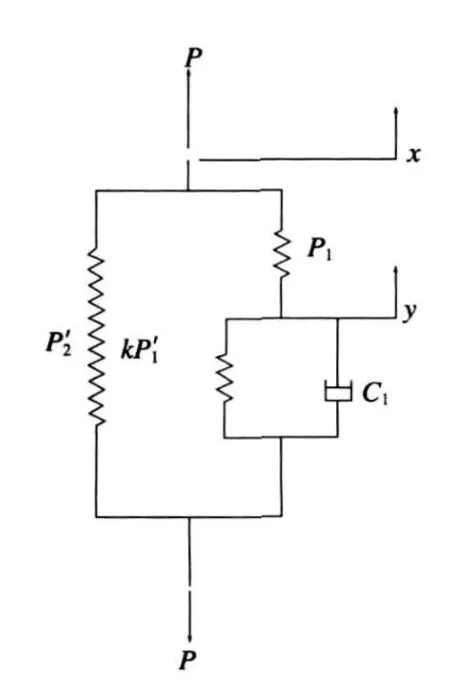
图2 有阻尼空气弹簧力学模型

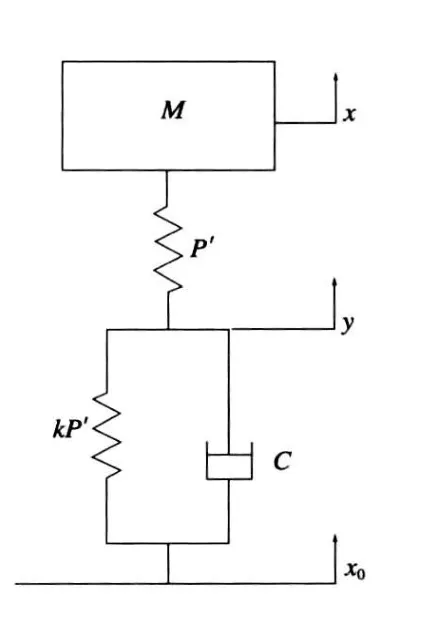
图3 有阻尼空气弹簧 悬挂的简化系统

1.2 空气弹簧悬挂系统有阻尼自由振动模型及其最佳阻尼

研究表明空气弹簧的阻尼作用主要取决于空气弹簧刚度P′和容积比k[1]。因此为使分析简化,可略去有效面积变化率的影响。空气弹簧悬挂系统有阻尼自由振动模型简化为图3所示力学模型。

该系统的自由振动方程为

求解式(11)微分方程可得对于任意容积比自由振动的最佳阻尼为

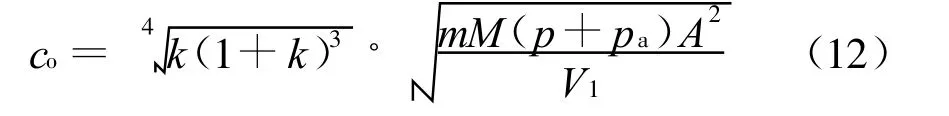
式中m为多变指数,p为空气弹簧内压,pa为大气压力,M为簧上质量(1/4车辆模型)。

多变指数m取决于变化过程的空气流动速度,对于车辆运行过程的实际情况来说,主要取决于振动时车体垂向运动速度。

1.3 空气弹簧悬挂系统有阻尼受迫振动模型及其最佳阻尼

对有阻尼空气弹簧悬挂系统在正弦干扰 x0=X0sin(ω t)的作用下的受迫振动方程为

同理,受迫振动的最佳阻尼为

2 阻尼系数测试方法与应用

阻尼系数测试方法主要有振幅衰减法、试验模态分析法和能量等效法。

2.1 振幅衰减法

振幅衰减法实际上是模态分析法中的时域法,直接由系统结构的时域自由响应求得自振频率、振型和阻尼等模态参数。

用振幅衰减法求阻尼系数,可表示为:

在实际测量振动曲线时,不可避免有外界噪声和测量误差的影响,研究表明这种方法测量的阻尼参数对振幅比的变化率非常敏感[2],难以保证测试的精度。

2.2 试验模态分析法

试验模态分析法是通过试验测定数据,确定阻尼等模态参数的。试验模态分析法属于频域法范畴,其中传递函数法分析过程如图4所示。对被测试件上的各点施加激励,同时测出其响应;接着用信号分析设备求出激励点和响应点的传递函数,并进行曲线拟合,计算出试件的自振频率、模态刚度、阻尼和振型等参数[3]。

图4 试验模态分析过程

上述方法,尽管测试精确度有所提高,但测试设备要求高,试验周期长,费用较高。

2.3 能量等效法

在第1.2节公式推导中未考虑结构的非线性,略去了空气弹簧有效面积率的影响。实际上对大多数悬挂用油压减振器和有阻尼空气弹簧的阻尼特性均具有很强的非线性。

对于一个非线性减振器要用线性的方法来处理,只有使其能量守恒才能精确地计算。其阻尼系数通常采用等效线性阻尼系数来描述。等效线性阻尼系数定义为在给定的行程和频率条件下,与一个非线性减振器相比,吸收同样能量的线性减振器的线性阻尼系数[4]。等效阻尼系数计算公式如下:

式中X为振幅;ω为角频率;vmax为系统振动中达到的最大速度;E为减振器在一个谐波周期吸收的能量;ceq为非线性阻尼器的等效线性阻尼系数。

试验外特性采用示功图P=f(s)的形式,则示功图封闭曲线所包围的面积,在数值上就是E值。

2.4 能量等效法在空气弹簧阻尼测试中的应用

以铁路干线 25T提速客车用某规格空气弹簧为例,用能量等效法进行了系统阻尼系数的测试。在振动台上通过试验做出系统的示功图,然后对示功图封闭曲线所包围的面积用专用软件进行积分求解,于是就可以通过式(16)计算空气弹簧系统的等效线性阻尼系数。

(1)阻尼系数ceq与内压p的关系

对有阻尼空气弹簧系统来说,如不考虑系统的非线性,从式(14)可知,空气弹簧阻尼系数ceq与内压 p和外大气压的和成线性关系。但从图5中试验数据曲线可以明显看出,空气弹簧阻尼特性的非线性。

图5 空气弹簧阻尼与内压的关系

(2)阻尼系数ceq与容积比k的关系

从图6中试验曲线可以明显看出,空气弹簧阻尼特性ceq与容积比k的非线性关系。

图6 空气弹簧阻尼与容积比的关系

3 结束语

对于具有非线性的有阻尼空气弹簧系统,用能量等效法求解系统的阻尼系数是一种相对有效的方法。它不仅对测试设备精度要求不高,方法简单易行,而且兼顾了系统非线性的影响因素。

在系统结构参数中,相对于其他参数来说,阻尼系数的识别精度是最低的。对于具有非线性的空气弹簧系统,这方面的研究和试验工作还尤为鲜见,因此有待进一步的研究。

[1] 张英会,郭荣生.弹簧[M].北京:机械工业出版社,1982.

[2] 贺向东,陈德成.阻尼系数时域识别的灵敏度分析[J].应用力学学报,1990,7(2):109-110.

[3] 卢文祥,杜润生.机械工程测试◦信息◦信号分析(第2版)[M].武汉:华中科技大学出版社,1999:329-320.

[4] 俞德孚,余志生,等.车辆悬架减振器的理论和实践[M].北京:兵器工业出版社,2003:64,77.