适于风险监测系统的零压缩二元决策图基本事件排序方法

汪 进,王 芳,王家群,顾晓慧,殷 园3,袁 润,李亚洲,胡丽琴,吴宜灿,FDS团队

(1.中国科学技术大学核科学技术学院,安徽 合肥 230027;

2.中国科学院等离子体物理研究所,安徽 合肥 230031;3.深圳大学理学院,广东 深圳 518000)

风险监测系统采用的实时风险模型是在基准风险模型的基础上升版得到,核电站的实际运行特点(比如需要考虑模型完备性、堆型特殊性等问题[1])导致了实时风险模型的自身的复杂性,而且风险监测系统需要对核电站风险水平进行实时分析计算,因此快速计算引擎发展是风险监测系统研发成功关键。

为了解决概率安全评价中超大规模故障树的求解问题,国内外专家进行了很多算法研究,包括二元决策图(BDD,Binary Decision Diagram)[2-3]、零压缩二元决策图(ZBDD,Zerosuppressed Binary Decision Diagram)[4-5],基本事件的排序[6-7]等。其中BDD算法引入使得求解大规模故障树成为现实,而ZBDD算法在此基础上又进一步提高了计算速度[4-5]。无论对于BDD还是ZBDD算法计算流程而言,基本事件排序都是必须,而且具有举足轻重地位的,因为排序将直接影响计算中间结果规模,并进而影响计算速度。

然而传统排序方法研究针对常规的故障树求解问题,并没有结合风险监测系统自身的特点,而且传统排序方法大多基于BDD,也没有结合ZBDD算法独有的特性加以改进。因而如直接利用传统排序算法则未能很好利用风险监测系统特点达到对于算法性能改良作用。本文在广泛调研基础上,同时结合了风险监测系统和ZBDD算法各自的特点,提出了一种可以有效提高风险监测系统实时风险计算引擎的计算速度的基本事件排序方法,并在FDS团队自主研发的概率安全分析软件RiskA[8]的计算引擎基础上开发出了风险监测系统计算引擎。实践表明这种基本事件排序方法可以有效减少ZBDD的规模,并进而提高计算速度。

1 基本事件排序方法

基本事件排序对ZBDD规模有较大影响,例如,最小割集{A,B,C},{A,B,D}按照A＜B＜C＜D排序得到的ZBDD(图 1)为“最小ZBDD”,按照C＜D＜A＜B排序得到的ZBDD(图2)为“最大ZBDD”。

图1 A＜B＜C＜D时的ZBDD结构Fig.1 ZBDD structure when A＜B＜C＜D

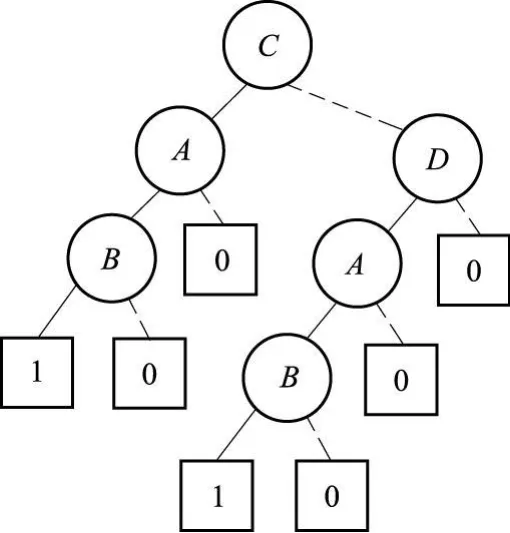
图2 C＜D＜A＜B时的ZBDD结构Fig.2 ZBDD structure when C＜D＜A＜B

“最小ZBDD”固然是基本事件排序算法追求的最好结果,但是寻找可以构造“最小ZBDD”的排序代价高昂,本文提出的算法能够以较小的代价得到一种基本事件排序,并且在此排序下的ZBDD较大程度逼近“最小ZBDD”。

本文提出的基本事件排序方法基本思路是：针对风险监测系统实时风险模型的初始状态,利用常规的ZBDD算法得到实时风险模型的定性分析结果,即最小割集;将割集中的基本事件按照其在所有割集中的出现频次从大到小排序并将排序信息应用到ZBDD算法中,再将改进后的算法用于该风险监测系统的日常运行。

将一组最小割集C的m个基本事件{E0,E1,…,Em-1}按照排序S依次记为Fi(i=0,1,2,…,m-1),则{F0,F1,…,Fm-1}是基本事件{E0,E1,…,Em-1}的一个排列,其对应关系为Fi=Exi(xi=0,1,2,…,m-1)。根据不同的基本事件排序可以将故障树转化为不同的ZBDD,将根据排序S得到的 ZBDD记为ZBDD-S,将Fi在 ZBDD-S中出现的频率记为Qxi。

下面从理论上分析排序S对ZBDD-S的规模的影响。

(1)按照ZBDD算法[9],ZBDD-S的第0层节点即头节点,一定是S中序号最小的基本事件,即F0(图3),则其在ZBDD中出现的频率Qx0=1。

图3 F0在ZBDD中的分布情况示意图Fig.3 F0's distribution in ZBDD

(2)F0将C分成两部分割集,一部分均包含基本事件F0,另一部分均不包含基本事件F0,F1在这两部分割集的分布可能有3种情况,如图3和图 4a、图4b所示,基本事件在ZBDD中的出现频率不会超过其在割集中出现的频率,所以Qx1=1或m in{2,Px1}。

图4 第1层节点F1在ZBDD中的分布情况Fig.4 F1's distribution in ZBDD

(3)Qx1的取值情况不同将会影响Qx2的取值。若Qx1=1,如图 4a所示,若Qx1=m in{2,Px1}=2,如图3所示,归纳以上两种情况可得Qx2=q2(q2=1,2,…,min{4,Px2})。

(4)设Qxk+1=qk+1(qk+1=1,2,…,min{max,Pxk+1}),为得到Qxk+1的取值,只需求其最大值max。在ZBDD中,记Fi接在Fj下的次数为Nj,i(i＞j),一方面,由于Fi序号仅大于F0～Fi-1,它只可能是F0～Fi-1的孩子节点,因此有

成立;另一方面,Fi的孩子数为2Qxi,因此有

成立。在给定Qx0～Qxk取值的情况下,当且仅当只有Fxk+1接在F0～Fk之下,而没有任何其他Fi(i＞k+1)接在F0～Fk之下时可以取到m ax值 ,由式(1)、式(2)可得

由式(3)、式(4)两式可得

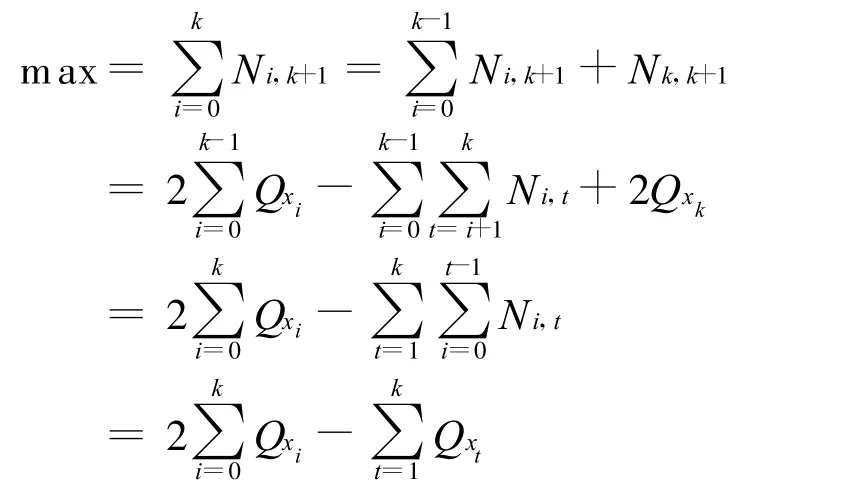
故有max=1+Qx0+Qx1+…+Qxk,若Qx0～Qxk均能取到相应的最大值,即20～2k,则 max=2k+1,所以Qxk+1=qk+1=1,2,…,min{2k+1,Pxk+1}。

(5)令Sk=Qx0+Qx1+…+Qxk,基本事件的排序S不同,Pxk的取值就不同,进而影响Qxk的取值,最终影响Sk的取值,这是基本事件排序对ZBDD规模影响的基本原因。

假设F0、F1、F2、F3在割集中出现的频率较大,即min{2k,Pxk}=2k,则它们的某种可能取值情况如表1所示。

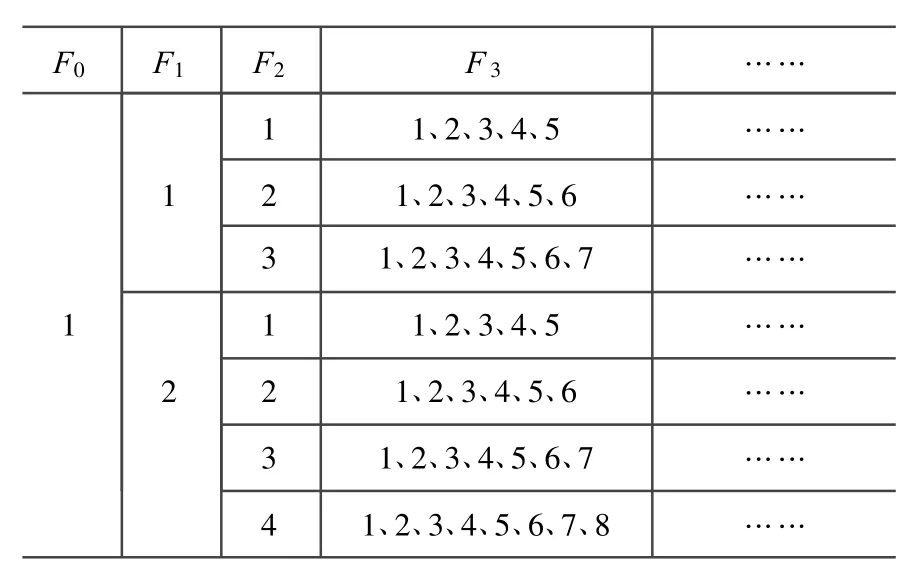
表1 ZBDD节点出现频率取值示例Table 1 Counts of a specific basic event in ZBDD

由此能够看出,当k值越大,Qxk可能取到的最大值min{2k,Pxk}=2k就越大,好在可以利用Pxk对该值进行约束,若将基本事件按其在割集中出现的频率排序,则随着k值的增大,Pxk逐渐减小,min{2k,Pxk}也将逐渐收敛,Sk=Qx0+Qx1+…+Qxk的值也会较大程度的向“最小ZBDD”趋近。

理论分析表明,将基本事件按照其在割集中出现的频率从大到小排列,可以使其对应的ZBDD较大程度的向“最小ZBDD”趋近,同时这种排序方法自身的代价很小。

2 结果与讨论

本文在FDS团队自主研发的概率安全分析软件RiskA的计算引擎基础上,应用上述基本事件排序算法开发出了适用于风险监测系统的计算引擎。测试中利用实际核电站风险监测系统基准状态的实时风险模型,与改进前的RiskA计算结果进行比较以测试排序算法的性能。改进前的RiskA采用的是传统的“深度优先、从左到右”的顺序依次对基本事件进行编号。例题描述见表2,测试结果见表3。

表2 例题描述Table2 Description of testexamp le

表3 性能测试结果Table3 Performance comparison between these twomethods

本文采用的测试例题均为实际电站规模。表2所示例题1为全电站模型,由57棵事件树链接而成,因而可以反映实际核电站运行的特点,其逻辑门和基本事件数目可反映其规模,因而同时能够验证算法的有效性;例题2是由大链接模型中前26棵事件树链接而成的故障树模型,例题3是后31棵事件树链接而成的故障树模型,从逻辑门数目和基本事件数目可以看出其规模均较大,能够有效验证本文提出的排序算法对同一套模型的不同覆盖范围的有效性。改进前RiskA的基本事件排序是基于启发式规则的排序方法[10],改进后RiksA应用了本文提出的排序方法,而基本事件的排序不同不会影响结果本身,这一点可以保证改进后RiksA的计算结果的正确性,从表3可以看出改进后RiskA的计算速度得到了较大的提升,在计算实际电站的大规模实时风险模型时表现出了较好的时间性能,运行时间约减少50%以上,在内存占用上也有所改善,降低约20%。

本文利用分析结果中基本事件出现的频率进行排序,反过来调整分析过程,可以减小最终分析结果ZBDD的规模,从而改善算法性能。将该方法应用于风险监测系统的实时风险模型分析,能加速模型分析计算的过程。对于风险监测系统在日常运行时的不同状态配置,故障树模型不会发生较大变化,使得每次分析过程的基本事件排序差别不大,因而该排序方法比较适合风险监测系统的实时风险计算。

3 结论

本文充分利用ZBDD结构及风险监测系统特点,提出了一套适用于风险监测系统的基本事件排序方法,并在FDS团队自主研发的概率安全分析软件RiskA的基础上结合该算法开发出了新的实时风险计算引擎,实践表明该方法能加速分析计算过程,从而满足风险监测系统实时分析需求。

[1] Risk O W,IAEA.Risk m onito r：a report on the state of the art in their development and use[R].2004.

[2] Sinnamon R M,Andrew s J D.New app roaches to evaluating fau lt trees[J].Reliability Engineering &System Safety,1997,58：89-96.

[3] Rauzy A.New A lgorithms for Fault-trees Analysis[J].Reliability Engineering&System Safety,1993,40：203-211.

[4] Woo Sik J,Sang H oon H,Jaejoo H.A fast BDD algorithm for large coherent fault trees analysis[J].Reliability Engineering&System Safety,2004,83：369-374.

[5] Woo Sik J.ZBDD algorithm features for an efficient Probabilistic Safety Assessment[J].Nuclear Engineering and Design,2009：2085-2092.

[6] Bouissou M.An ordering heuristic for building binary decision diagram s from fault-trees[J].Annual Reliability and Maintainability Symposium, 1996：208-214.

[7] Ibanez-Liano C,Rauzy A,Melendez,et al.Variable ordering techniques for the application of Binary Decision Diagrams on PSA linked Fau lt Tree models[J].2009.

[8] 吴宜灿,刘萍,胡丽琴,等.大型集成概率安全分析软件系统的研究与发展[J].核科学与工程,2007,27(3)：270-276.

[9] Minato S.Zero-suppressed BDDs for setmanipulation in combinatorial problems[C]//DAC'93：30th ACM/IEEE-CSDesign Automation Conference,Dallas,TX,1993：272-277.

[10] 刘萍,吴宜灿,李亚洲,等.一种基于ZBDD求解大型故障树的基本事件排序方法[J].核科学与工程,2007,27(3)：282-288.