电成像测井仪器中ADC-BIST测试方法研究及实现
赵建武,师奕兵,王志刚
(电子科技大学自动化工程学院 成都 610054)
电成像测井是近年来发展较为迅速的测井新方法。电成像测井仪器能提供重要的地质结构和地质构造的特征信息。为了保证仪器可靠工作,必须对仪器的混合信号电路进行有效的测试,而对电路中的模拟数字转换器(ADC)的测试尤为重要。
目前,混合信号自动测试设备非常昂贵,对ADC采用内建自测试技术(BIST)不但可以降低总体测试成本,而且便于在测井现场对仪器进行测试和故障定位。文献[1-3]提出了ADC参数的直方图测试方法,测试激励使用正弦信号,所得到的ADC输出代码分布不均匀,参数计算比较复杂,内建自测试硬件资源开销较大。文献[4-6]中对直方图测试方法做了改进,测试激励使用三角波信号,尽管该方法具有均匀的代码分布和相对较少的存储资源需求,但为了计算码宽仍需要相当大的存储空间。一种被称为“时间分解”的参数优化算法被提出,用于解决存储问题。但“时间分解”算法使ADC测试时间随其分辨率成指数上升。还有其他对ADC的设计和测试方面的研究成果不断见之于报导[7-10]。
本文针对ADC测试存在的问题,论述了一种新颖的ADC内建自测试方法,从电成像测井仪器中不同配置的电路模块的测试需求出发,给出了两种完整的ADC板级内建自测试结构。与目前常用的ADC测试方法相比,该方法不仅能简化测试过程,提高测试速度,并且所需要的硬件测试开销较小。优化的ADC测试电路对电成像测井仪器中原有的电路干扰较小,实验数据分析和实际工程应用证明了该方法的有效性。
1 ADC静态参数测试
在混合信号电路测试中,不需要对被测电路所有的参数进行测试,相同的电路模块可以在不同的设计中被复制使用,而在不同设计应用中的功能差异决定需要被测试的参数。对于电成像测井仪器电路,ADC的静态参数比动态参数更加重要,最关键的静态参数包括差分非线性误差(DNL)、积分非线性误差(INL)、输入失调(offset)、增益误差(gain error)和漏码(missing codes)。
ADC的输入信号源和输入通道不可避免地会产生噪声,电成像测井仪器电路中ADC模型如图1所示。

图1 电成像测井仪器电路中ADC模型
不失一般性,本文假设ADC输入通道中的噪声幅度具有高斯分布的概率特性,输入信号中的噪声幅度为均匀分布。由于量化误差,ADC的输入电压和输出码字是多对一的映射关系,而噪声使码字之间的码边位置(code edge)具有不确定性,因此,码边位置的计算具有概率统计特性。为了把ADC的多对一的输入/输出映射关系转化为一对一的映射关系,需要通过测量码宽计算码边位置,码宽(code width)为:

式中VUE和VLE分别表示全‘1’和全‘0’码字的码边电压值,可以用折半搜索(binary search)或伺服方法(servo method)获得。通常ADC静态参数的计算使用端点法,这对DNL和INL的影响较小,但对输入失调和增益误差影响较大。该方法的优点在于可用比较简单的硬件电路实现。使用最佳拟合曲线计算VLSB可以较为全面地刻画ADC的转换曲线的特性。码边最佳拟合曲线(B)是与被测码边值和理想码边值具有最小均方误差的一条曲线,表示为:
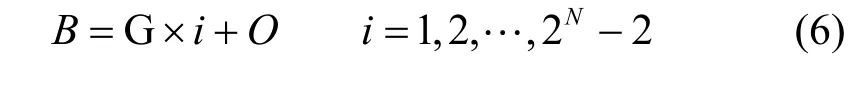
可通过计算被测码边曲线与最佳拟合曲线相对于斜率和偏移量偏导数的极值方法求得曲线的斜率:

最佳拟合曲线的斜率就是ADC的增益,如果被测ADC为双极性ADC,曲线偏移量就是ADC的输入失调,对于单极性ADC,曲线在i=(2N-2)/2时的值为ADC的输入失调。测试激励信号的选择与ADC的结构和被测参数有关,使用正弦信号有利于动态特性参数的测试,对于包含模拟比较器的ADC,三角波信号可有效消除比较器的迟滞效应对DNL和INL的影响,线性斜坡信号能产生均匀的代码分布,该特性可以减少内建自测试的硬件开销。本文采用线性斜坡信号作为测试激励信号。
从式(1)~式(5)可知,测量H(i)的目的是为了得到码字的码宽值和码边绝对电压值。本文使用码字跳变检测器和计数器直接测量码宽,对一个给定的缓慢变化斜坡输入信号,码宽与码字输出所占用的时间成正比,码宽值可以使用计数器记录,随着斜坡信号扫过ADC的输入端,ADC输出码字发生变化,计数器的值被更新。码字的跳变可以使用简单的XOR和OR网络检测。ADC的输出码字随斜坡信号单调线性变化,因而漏码被检测。本文认为,当一个码字宽度小于0.1 LSB时,漏码发生。如图1所示,由于噪声的存在,对于一个给定的输入电压可能无法确定ADC的准确输出;此外,噪声还会影响码宽值的测量,因此可以通过对ADC多次施加测试激励,以减少噪声的影响。
2 内建自测试结构
内建自测试技术可以用于芯片级或板级等不同的设计层次。本文所论述的ADC内建自测试技术是指在板级的应用。很多ADC的测试方案需要DAC、存储器和DSP等器件支持,而且不能测试ADC的漏码,应用具有一定的局限性。本文给出了两种完整的ADC测试结构,分别用于电成像测井仪器中不同配置的电路模块。
(1) 如果被测ADC所在电路具有存储器和DSP处理器,ADC内建自测试结构如图2所示。图中,虚线框内为原设计的已有部分,DSP对数据存储器的写入操作只发生在每次码字改变的时刻,测试控制模块主要由一个有限状态机构成,通过不同状态产生ADC测试控制信号。
设计电成像测井仪器电路时,ADC与DSP之间使用串行数据传输机制,为了提高DSP效率,设计时还采用FIFO对ADC输出数据进行缓存,串并转换和FIFO使用FPGA芯片实现。为了减小额外的测试硬件资源开销,ADC的码字跳变检测和码宽计数由DSP软件完成。
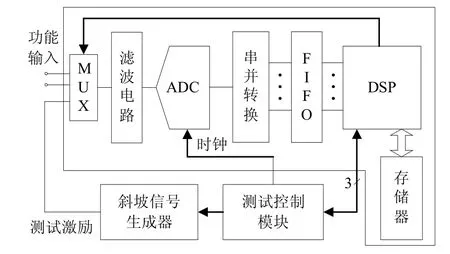
图2 ADC内建自测试结构1
(2) 如果被测ADC所在电路不具备存储器和DSP处理器,ADC内建自测试结构如图3所示。图中,移位寄存器组由3个部分组成,分别用于存储码宽值、ADC输出码字和码字计数器值。如果被测ADC没有漏码,码字计数器值与当前ADC输出码字具有相同的数值。在对新的码字宽度的计数过程中,移位寄存器中的数据被扫描输出。使用外部数字信号自动测试设备分析测试数据。
码字位翻转检测器可由移位寄存器和XOR-OR网络组成,移位寄存器用于存储前一个ADC的输出码字,XOR-OR网络实现按位比较功能。为了满足测试要求,码宽计数器的宽度要考虑HPC(hits-percode)和最大DNL的限制。码宽值并非越宽越好,代码计数器宽度应与ADC输出码字位宽相同。
相关研究提出使用片上简单的硬件电路实现ADC参数计算,计算方法依赖ADC的端点码字,但不能全面反映ADC输入/输出转换曲线的特性。随着数字信号自动测试设备成本的下降以及混合信号电路测试壳(ADC-DAC对)研究的发展,使用数字信号自动测试设备对混合信号电路进行测试已成为新的发展趋势。

图3 ADC内建自测试结构2
3 实验结果与分析
本文对电成像测井仪器电路中ADC的测试实验结果进行分析,测试时间和测试硬件资源开销主要由ADC的分辨率和测试方案的精度决定,对于一个待测试的ADC,用作测试激励的斜坡输入信号的频率为:

式中Fsampling表示ADC采样频率;HPCaverage表示斜坡信号扫过ADC的输入时每个输出码字出现的平均次数;N表示输出码字的位宽。
测试输入斜坡信号频率为1 kHz,如果HPCaverage取值为16,ADC的采样频率为4.096 MHz。为了提高测试精度,降低噪声的影响,除了利用原有ADC输入通道的滤波电路(如图2和图3所示),还可对ADC多次施加测试激励,总的测试时间为:
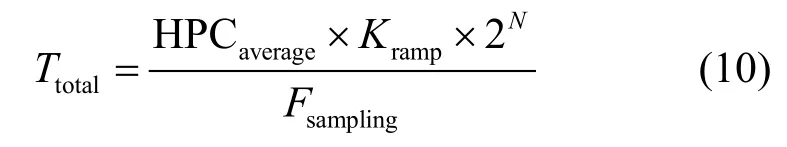
式中Kramp表示斜坡信号的周期数。HPC、噪声和斜坡信号的线性度是影响测试精度的主要因素,因此总的误差为:

式中Nramp表示斜坡信号的线性度。ADC输入信号和输入通道中的噪声幅度n具有高斯分布的概率特性,噪声幅度均值为0,标准偏差为σ,如果输入信号与码边电压的差为ΔV,由噪声所引起的误码产生的概率为:

如式(11)所示,总的误差由3个部分组成,当εNL为0.031 25时,Nramp-NADC=5;HPC=(HPCaverage×Kramp)超过 160 时,εNL已经远远大于εHPC。因此,增加 HPC可以减小εHPC,当εHPC超过一定界限后将不再有助于整体测试精度的提高。
被测ADC的差分非线性(DNL)和积分非线性(INL)分别如图4和图5所示。

图4 ADC差分非线性(DNL)

图5 ADC积分非线性(INL)
可以看到DNL的最大绝对值为0.28 LSB,INL的最大绝对值为0.32 LSB,都没有超过±0.5 LSB。对于ADC,差分非线性和积分非线性存在的转换关系为:

因此积分非线性的值可由计算差分非线性的值直接得到。作为对比,使用直方图方法对ADC的静态参数进行分析计算。测试激励采用1 kHz的正弦信号,ADC的采样频率仍为4.096 MHz,正弦测试激励信号下每个码字理想平均HPC分布分别为:

式中OS为偏移量电压值;P为峰值电压值;Hsampling(i)为4.096 MHz正弦激励信号下的HPC。直接码宽测量与基于直方图ADC静态参数测试的比较结果如表1所示,其中差分非线性误差和积分非线性误差取最大绝对值。

表1 直接码宽测量与直方图测试结果比较
由表1可知,两种方法所得到测试结果基本一致,ADC静态参数测量值之间的差值小于0.05 LSB。
4 结 束 语
本文论述了一种直接测量码宽的顺序ADC静态参数分析方法,该方法还可以测试ADC的漏码特性,与直方图分析方法不同,不需要测量码字频次,可有效减少测试硬件资源开销。本文还根据电成像测井仪器电路不同配置的测试需求,给出两种不同的ADC内建自测试测试方案,从实现技术来看,如果系统具有存储器和DSP,该方法在保证精度和测试时间的前提下,可减小对存取速度和存储空间的需求;如果系统没有存储器和DSP,与已有的技术方法相比,具有非常短的测试时间开销,而且内建自测试硬件实现比较简单。综上所述,本文方法可以实现对ADC静态参数的有效测试,具有工程实用性。
[1] LU A K, ROBERTS G W. An analog multi-tone signal generator for built-in self-test applications[C]//Proceedings of IEEE International Test Conference (ITC). Washington D C: [s.n.], 1994: 650-659.
[2] LU A K, ROBERTS G W, JOHNS D A. A high-quality analog oscillator using oversampling D/A conversion techniques[C]//Proceedings of IEEE International Symposium on Circuit and System. London: [s.n.], 1994:1298-1301.
[3] BLAIR J. Histogram measurement of ADC nonlinearities using sine waves[J]. Proceedings of IEEE Transaction on Instrumentation and Measurement, 1994, 43(3): 373 - 383.
[4] AZAIS F, BERNARD S, BERTRAND Y, et al. A low-cost BIST architecture for linear histogram testting of ADCs[J].Journal of Electronic Testing: Theory and Applications,2001, 17(2): 139-147.
[5] AZAIS F, BERNARD S, BERTRAND Y, et al.Implementation of a linear histogram BiST for ADCs[C]//Proceedings of IEEE Conference on Design,Automation and Test in Europe (DATE). Munich, Germany:[s.n.], 2001: 590-595.
[6] RENOVELL M, AZAIS F, BERNARD S, et al. Hardware resource minimization for a histogram-based ADC BIST[C]//Proceedings of the 18th IEEE VLSI Test Symposium.[S.l.]: [s.n.], 2000, 247-252.
[7]朱彦卿, 何怡刚, 阳 辉, 等. 一种高速ADC静态参数的内建自测试结构[J]. 湖南大学学报(自然科学版), 2007,34(10): 62-65.ZHU Yan-qing, HE Yi-gang, YANG Hui, et al. A high-speed BIST architecture for ADC parameter testing[J]. Journal of Hunan University (Natural Sciences)2007, 34(10): 62-65.
[8] 张建强, 冯建华, 冯建科. 基于自动测试系统的ADC测试开发[J]. 仪器仪表学报, 2007, 28(2): 279-283.ZHANG Jian-qiang, FENG Jian-hua, FENG jian-ke. Testing development for ADC on automatic test system[J]. Chinese Journal of Scientific Instrument, 2007, 28(2): 279-283.
[9] 程梦璋, 景为平. 新型流水线ADC的设计与分析[J]. 电子科技大学学报, 2008, 37(6): 930-933.CHENG Meng-zhang, JING Wei-ping. Design and analysis of a novel pipelined ADC[J]. Journal of University of Electronic Science and Technology of China, 2008, 37(6):930-933.
[10] 王向展, 宁 宁, 于 奇. 新型分段多分搜索算法高速A/D转换方案[J]. 电子科技大学学报, 2008, 37(1): 61-64.WANG Xiang-zhan, NING Ning, YU Qi. A novel high-speed A/D conversion scheme based on segmented multi-division search algorithm[J]. Journal of University of Electronic Science and Technology of China, 2008, 37(1):61-64.

