水位统计法推求河道高程之探讨
李全卫,李志为 ,冯 涛,杜庆有
(1.河北省唐山市海港开发区供水工程管理处,063611,唐山;2.天津市海河管理处,300400,天津;3.河北省水利水电勘测设计研究院,300250,天津)
在天津市水利工程体系中,由于历史的原因,存在着不同高程系统同时使用的情况,例如大沽基面、黄海基面,给天津市的水利工程以及相应的管理工作带来了许多不便。为了解决这一问题,笔者在统计分析海河干流水文控制站现有资料的基础上,对现有水文站点引用的基准点高程作出“冻结”,所引起的数据差异进行判读,然后选定调整参数,以期得到修正后的水位数据。
一、条件与假设
要想得到同一河流不同水准点高程之间的换算关系,并取得相关的修正数据,需要具备以下条件:
①水体连通性。所在水文站的水位必须在无节制、自由连通的水体中,如海河二道闸、耳闸、西河闸水文站。屈家店水文站由于在北洋园有橡胶坝阻拦,使其控制的水体不是与其他几个水文站控制的水体相连通,所以不符合上述条件。同样,由于受到二道闸阻隔,海河闸水文站也不符合上述条件。但屈家店和海河闸水文站可通过间接换算的方法来消除非连通性的影响,如北运河北洋园橡胶坝的上下游水位都是根据同一个引据水准点引测的,可对节点上下游两段水体的水位进行换算后,再折返至引据水准点,就可以渐次地换算至北运河屈家店水文站。
②水体运动平稳。水体流动平稳,有较为稳定的水头差和水面线,这时可假定上下游水面基本相平。
③水体水面面积不宜过大。水面面积过大,尤其是水面广、水深大的水域,极易受到风力、入出流和水体内外部循环的影响,使水面始终处在动态平衡中,水面各点水位不同,难以保证精度。
二、用水位统计法推求河道高程关系的一般方法介绍
1.分析样本,取用时间段的选择
这里所指的样本,主要是水位数据的选取。在选择样本时应尽量选择受外界因素影响较小的样本,还要注意样本的一致性、趋势性和随机性。
为了排除风力、大规模入出流的影响,在样本选择时,对于稳定流水体,应取河段内各断面均处于同一稳定流量、稳定水位,且水位流量为单值关系时的水位样本。鉴于天津市的特殊情况,海河干流与大多数河道在非汛期都处于相对静止的状态,所以这是最佳的样本选择时间段。
2.上下游水文站水位样本的变异差控制
由于种种原因,所选取时间段内的水位样本以及由此而产生的上下游水位差样本,不可避免地存在一些个别的突变现象,也就是水位数据的不合理变异所引起的水位差不合理变异,因此需要将这些不合理变异的水位以及水位差样本从样本总体中剔除。
具体的做法是先对某一时间段内的水位差样本总体用算术平均法计算出其均值,然后检查均值与单个水位差样本之间的变异差。将允许变异差值控制在正负5 cm范围内,并将超出允许变异差值范围的单个样本从样本总体中予以剔除。接着,对剩余的单个样本再进行上述的计算分析,直至所有的单个样本与均值的变异差都控制在正负5cm范围内。同时对剩余单个样本的数量进行进一步检验。
3.统计计算
在完成上述步骤的情况下,用最小二乘法迭代计算,确定上下游水文站之间在上述特定情况下的误差最小的水位差值,结合考虑合理的水面线的情况下,该差值就可以作为读取水位的水尺零点高程的修正值,进而作为引据水准点高程的修正值。
以此类推,当一条河流有多个水文站时,即可计算出两点水位差值及多点水位差值,并将其相应作为读取水位的水尺零点高程的修正值,进而作为对应高程的修正值。

表1 最小二乘法迭代计算表单位:m
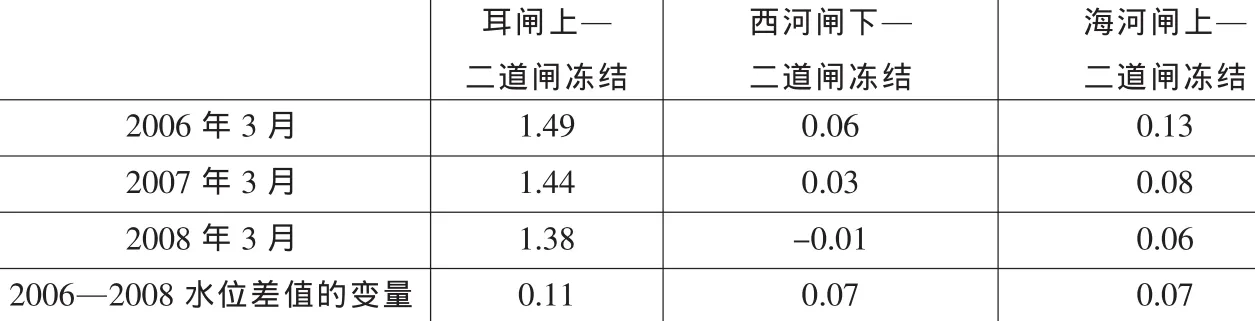
表2 2006—2008年统一高程计算表 单位:m
三、海河干流应用实例分析
将海河干流分成三段:屈家店闸—北洋园橡胶坝 (此段不符合计算条件),北洋园橡胶坝、西河闸—海河二道闸,海河二道闸—海河闸。
1.样本的选取
冬季海河入出流较小、蒸发量较小,使河道水位变化较小,所以较为适宜开展统计工作,但又考虑到每年12月、1月、2月为冰冻期,可能会对计算产生影响,故本次统计选取时段为 2008年 3月 1—31日,二道闸、耳闸、西河闸、海河闸水位资料作为样本进行计算。其中,由于二道闸、耳闸为每日8时、16时上报水位,西河闸、海河闸为每日8时上报水位,故统计的样本容量分别为62和31。
2.推求过程
①基准面选择。由于在防汛调度中是以二道闸水位(二道闸冻结高程)为依据,故以其为基准,固定不变。
②计算水位差。2008年3月1—31日,分别计算二道闸水位与耳闸、西河闸、海河闸水位差,并计算水位差的平均值。
③统计计算。分别求得二道闸水位与耳闸、西河闸、海河闸的水位差作为统计样本,计算各水位差均值作为初始值,经过一次平均比较耳闸0、西河闸1、海河闸样本中分别有0个、1个、0个样本不符合正负5cm的要求,故样本总体符合75%样本合格的总体要求。
对样本总体运用最小二乘法进行迭代法计算,确定误差最小的水位差值,计算结果见表1。根据计算结果,即当水面静止时二道闸闸上水位(二道闸冻结高程)为2.00m,耳闸水位应为3.38m,西河闸水位应为1.99m。耳闸水位为4.00 m时换算成二道闸冻结高程应为2.62 m,西河闸水位为2.00m时换算成二道闸冻结高程应为2.01m。
根据以上计算方法,可以计算出2006、2007、2008 年三年的水位换算结果,如表2。
由计算结果明显可见,每年的计算结果呈趋势变化,这与不同地区及河段的沉降不均匀有关,故如要得到与实际较为接近的河道高程及水位换算关系,需及时更新计算。
[1]杨爱民,唐克旺,王浩,等.生态用水的基本理论与计算方法[J].水利学报,2004(12).
[2]徐志侠,陈敏建,董增川.湖泊最低生态水位计算方法研究[J].生态学报,2004,24(10).
[3]刘昌明.21世纪中国水资源若干问题的讨论[J].水利水电技术,2002(33).
[4]姜德娟,王会肖.生态环境需水量研究进展应用[J].生态学报,2004,15(7).

