碳酸盐岩生物礁储层的流体替换研究

宋洪勇,熊晓军林 凯,李 扬 (成都理工大学地球探测与信息技术教育部重点实验室,四川成都610059)

生物礁是由原地生长的造礁生物所营造的具有抗浪格架、外形呈凸透镜状的碳酸盐隆[1]。生物礁是良好的油气聚集场所,具有孔隙度高、储量丰度大、油气产能高等特点,在油气勘探开发中具有十分重要的地位。目前对于生物礁的数值模拟大多采用褶积方法,但该方法不能有效地反映生物礁地震波场的运动学和动力学特征,也不能反映不同流体类型与不同孔隙度储层的地震波场特征[1]。Gassmann(1951)导出了流体饱和岩石有效体积模量与骨架体积模量、干燥岩石体积模量、孔隙流体体积模量、以及孔隙度之间关系的著名Gassmann方程[2]。以Gassmann方程为理论基础的流体替换容易实现如下过程:①从一种流体饱和岩石的地震波传播速度预测另外一种流体饱和岩石的地震波传播速度。②用岩石骨架地震波传播速度预测饱和岩石地震波传播速度,再结合常规的波动方程数值方法即可实现双相介质的地震数值模拟[2]。当前大多数流体替换研究重点集中在碳酸盐岩石由一种饱和状态到另一种饱和状态的替换[3],笔者利用研究区的碳酸盐生物礁干岩样,探讨由干岩石到饱和岩石的流体替换过程,并提出一种新的基于Gassmann方程的流体替换的计算流程,用于分析碳酸盐生物礁地震响应特征随流体饱和度及孔隙度变化的关系,进行岩性和油气预测。

1 方法及原理

1.1 Gassmann方程

Gassmann方程是各向同性介质流体替换的理论基础[2]。流体替换的目的是在给定的储层条件 (例如温度、压力、孔隙度、岩石基质 (骨架)类型和盐水矿化度)和孔隙流体饱和度条件下模拟储层的纵横波速度和密度。Gassmann方程则是把岩石孔隙度、框架和流体性质与岩石体积模量联系起来的桥梁。

Gassmann方程的基本假设条件是:①岩石 (基质或骨架)宏观上是均质的;②所有孔隙都是连通或相通的;③所有孔隙都充满流体 (气、液或气液混和物);④研究中的岩石-流体系统是封闭的 (不排液);⑤孔隙流体不对固体骨架产生软化或硬化的相互作用。下面是Gassmann方程的一种表达式:

式中,Ksat为饱和岩石的有效体积模量,GPa;KfL为岩石内孔隙流体自身的体积模量,GPa;Kma为岩石基质(骨架)矿物的体积模量,GPa;Kdry为干燥(空孔隙)岩石的有效体积模量,GPa;φ为岩石的有效孔隙度。

利用式 (1)和相应其他公式可以实现流体替换。Gassmann方程可以得出岩石的体积模量如何随岩石中孔隙流体的变化而变化。换言之,在岩石和岩石有效孔隙度不变的情况下,已知含流体1的饱和岩石的有效体积模量,可求得 (或预测)含流体2的饱和岩石的有效体积模量[4]。

1.2 利用Gassmann方程进行流体替换的计算步骤

1)计算含流体1的饱和岩石的有效体积模量和拉梅常数 饱和岩石的有效体积模量和拉梅常数的计算公式如下:

2)计算含流体2的饱和岩石的有效体积模量 由式(1)可得出:

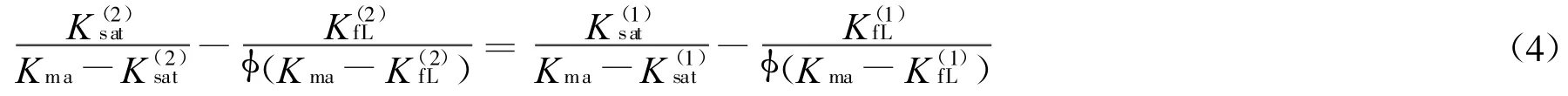
3)确定含流体2的饱和岩石的拉梅常数 含流体2的饱和岩石的拉梅常数与含流体1的饱和岩石的拉梅常数相等,即:

4)计算含流体2的饱和岩石的密度 饱和岩石的密度计算公式如下:

5)计算含流体2的饱和岩石的波速 饱和岩石的波速计算公式如下:

2 实例分析

表1是关于图1的测井解释表,该井在目的层段共解释了15个层段 (包含气层、差气层、气水同层)。从表1中可以看出,解释得到的气层5、6、7、8不仅位置紧紧相邻,而且速度差异也较小。因此,在以下的流体替换中,将这4个气层同时进行流体替换,从而研究其地震响应特征。

表1 W05井的测井解释表

图2是基于W05井建立的水平地层模型,该模型将表1中的15个解释层段设定为均匀层 (其厚度与解释层段的厚度相同),模型的其他地方均为厚度为1m的薄互层,模型的速度和密度全部根据声波和密度测井曲线设定。

在以下的数值模拟中,采用如下流程[5,6]:①对原始模型采用波动方程数值模拟方法进行正演模拟,并与W05井的井旁地震记录相比对,迭代修正模型的各项参数 (初始延拓深度、初始延拓速度、子波频率等参数),得到与地下模型相一致的速度模型。②采用计算得到的速度模型进行流体替换的正演模拟,分析不同流体与不同孔隙度的储层的地震反射特征。

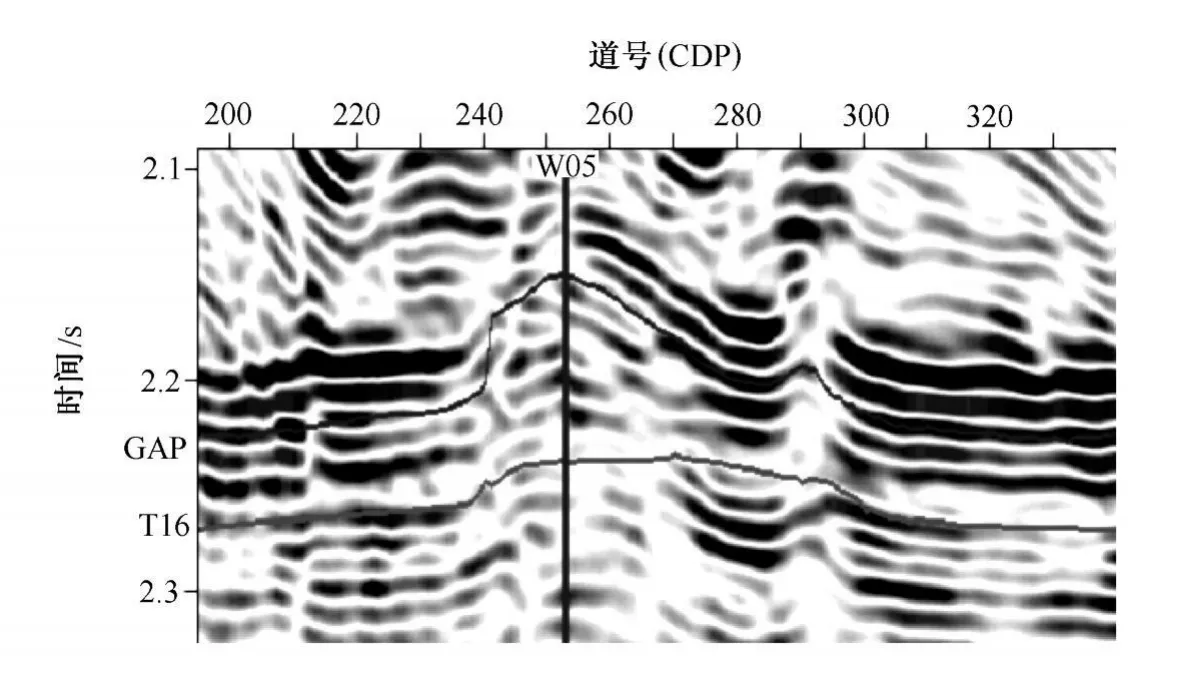
图1 某区生物礁W05井的地震剖面 (生物礁介于G AP层与T16层之间)

图3是对图2中的模型进行波动方程正演计算得到的模拟记录,替换气层的综合反射表现为模拟记录中的第2个波峰反射,从图3中可以看出,模拟记录与图1中W05井的井旁地震记录具有很好的一致性 (除第3个波峰反射位置偏上,第4个波峰反射能量较强),从而验证了正演模型的各项参数的可靠性与正确性。

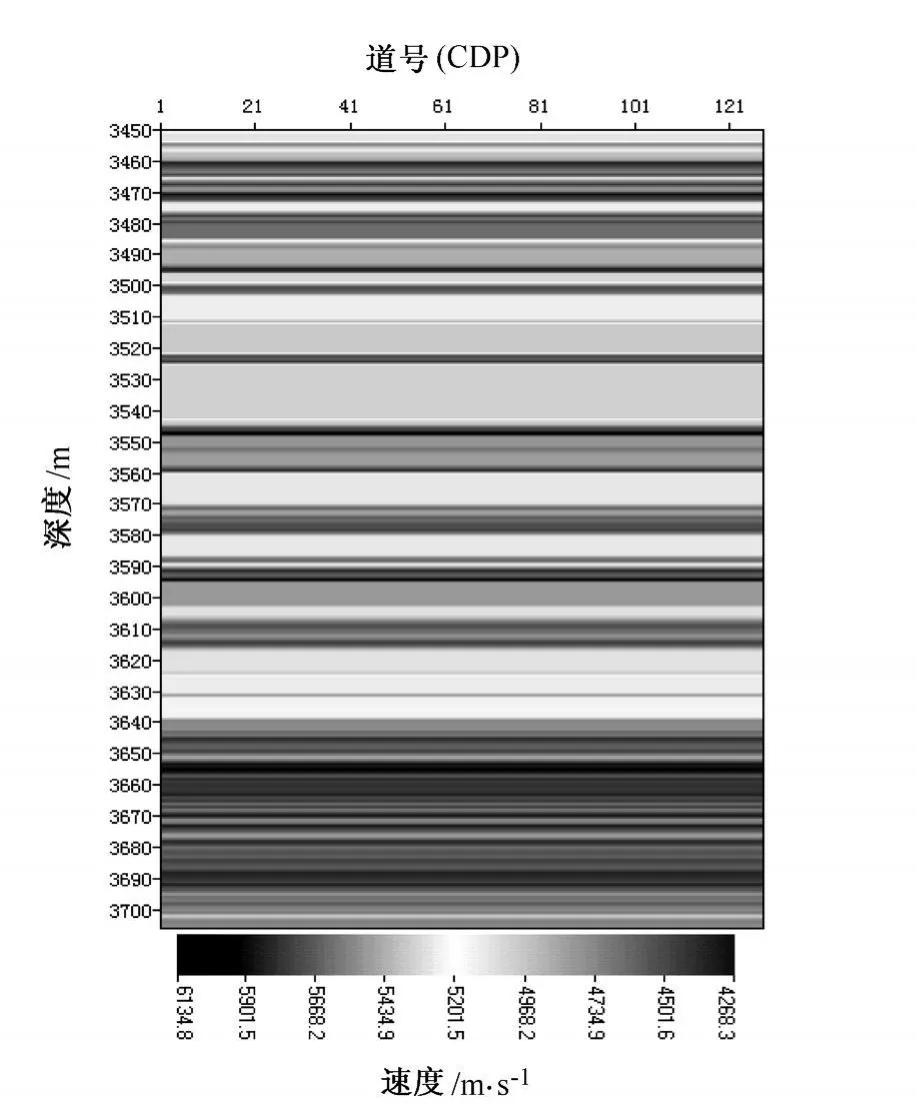
图2 基于表1的测井解释数据建立的水平地层模型

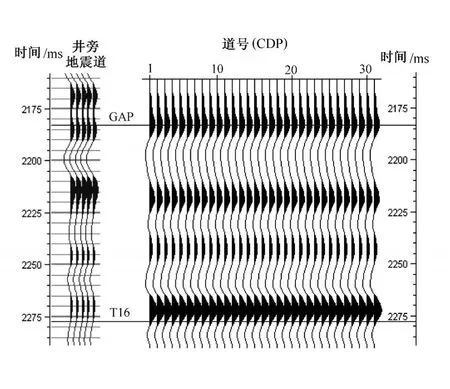
图3 对应图2模型的正演记录

图4是将气层替换为水层 (孔隙全部充填水)和干层的模拟记录,替换后的水层的反射表现为图4(b)中的第2个波峰反射,其相对于图4(a)而言,仅表现为略微的振幅减弱,其他特征完全一致。其主要原因在于,气层替换为水层后,其等效速度略微变大,从而与围岩速度差异减小,从而导致反射界面能量减弱。干层等效于致密层,即替换后的生物礁储层气层消失,其等效速度为高速。因此,在图4(c)中的模拟记录上出现了第2根同相轴的急性反转,并且导致第1根同相轴的波形分裂为2个波峰,以及第3根同相轴的能量减弱,波形也发生了变化。

图5是将气层孔隙度提高至8%和10%得到的流体替换的模拟记录,从图中可以看出,随着孔隙度的增加,气层的等效速度降低,其与围岩的速度差增大,其反射能量逐渐增强。由此可知,高孔隙度的气层表现为强的亮点反射。

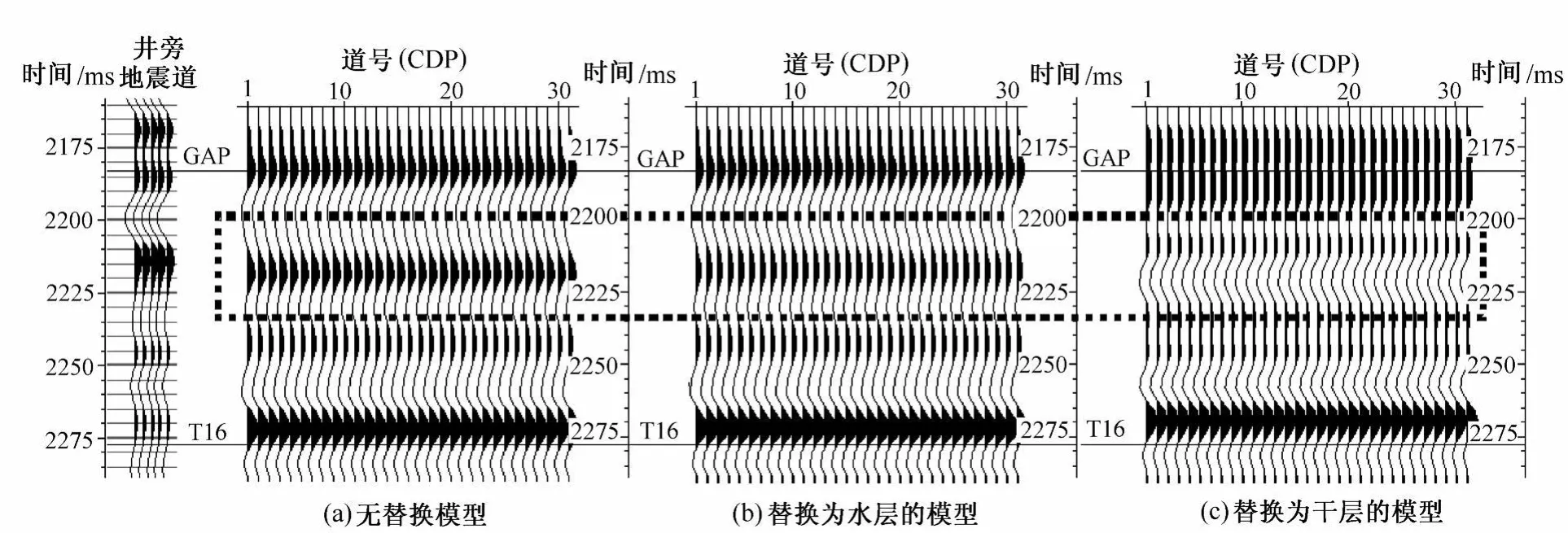
图4 不同流体类型的流体替换

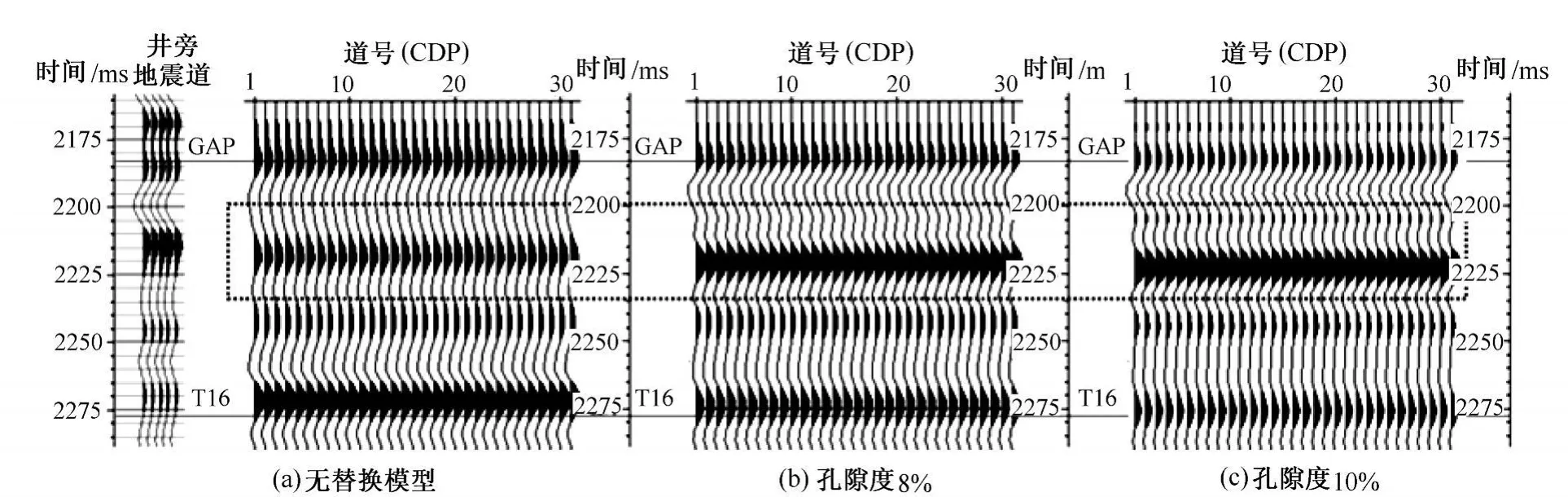
图5 不同孔隙度类型的流体替换

3 结 论

1)基于Gassmann方程的流体替换的计算流程可以有效地模拟不同流体类型和不同孔隙度的碳酸岩生物礁储层的地震响应特征。

2)对于碳酸盐岩生物礁储层,随着孔隙度的增大,高孔隙度的气层表现为强的亮点反射。

3)当改变碳酸盐岩生物礁储层内部流体性质时,储层的等效速度会发生急剧变化,会导致地震反射同向轴的波形分裂或极性反转。

[1]熊晓军,贺振华,黄德济.生物礁地震响应特征的数值模拟[J].石油学报,2009,30(1):75～79.

[2]史燕红.基于Gassmann方程的流体替换 [D].成都:成都理工大学,2009.

[3]林凯,贺振华,熊晓军,等.基于Gassmann方程的鮞滩储层流体替换模拟技术及其应用 [J].石油物探,2009,48(5):493～498.

[4]贺振华.岩石物理学讲义[M].成都:成都理工大学,2008.

[5]贺振华.反射地震资料偏移处理与反演方法 [M].重庆:重庆大学出版社,1989.

[6]熊晓军.单程波动方程地震数值模拟新方法研究[D].成都:成都理工大学,2007.