温控参数有限元法在边坡稳定分析中的应用
曾 逸
(双流县水务局,四川双流,610200)
1 引言
目前边坡工程中常用的稳定分析方法是基于极限平衡原理的传统方法。传统稳定分析方法积累了丰富的经验,成果可靠。但是由于传统方法做了很多假设和简化,例如需要假设滑裂面的位置、不考虑条分土体内部的应力应变关系等,不能得出滑坡体真实的应力和变形。
近年来,不少研究者尝试采用有限元方法来进行边坡的稳定性分析。有限元法能全面满足静力平衡条件、应变相容条件和非线性本构关系,可以不受边坡形状不规则、材料不均匀的限制,不需预先假定滑裂面,能模拟滑坡的可能运动方向,确定破坏区的位置和破坏发展情况。
由于许多边坡通常并不受到表面分布载荷的作用,目前大多数学者是通过土体抗剪强度参数的折减而超载使边坡达到极限状态的。即假定实际的土体强度参数(内聚力及内摩擦角)折减某一倍数 Fs后,作为一组新的材料参数代入进行有限元计算,并判断边坡在完成全部加载过程之前是否达到极限状态。如果经过某个 Fs值的折减能够使边坡达到极限状态,而经过比该值稍小的Fs值的折减不能使边坡达到极限状态,此时的 Fs即为安全系数。通过这种方法还可以同时得到临界滑裂面的位置。
在通常的有限元分析程序中,材料参数是需要在输入文件中给定的。为了按照上述方法确定折减系数,需要修改输入文件中的 c和f值进行反复的试算。显然,为了求得安全系数,计算量大,即使采用二分法,一般也需要计算 10次左右[1]。
另一种作法是,首先按照实际的强度参数指标进行模拟计算,完成全部的加载过程后,再分步降低土体的强度参数值进行迭代计算,直至边坡进入极限状态,由此得出相应的安全系数[2]。这种作法应该更加符合实际情况,而且整个分析过程是一次完成,不用修改输入文件反复试算。但是,文献[2]所采用的方法需要调整屈服面并修正应力,从而计算体系的不平衡力。这些算法都需要重新编制有限元程序才能实现。本文利用大多数通用有限元软件(如 ABAQUS)中都具有的可使材料参数随温度变化的功能,用温度场控制强度参数变化来实现参数的连续折减。这样作不仅能最大限度地利用 ABAQUS本身所具有的计算精度高、非线性求解能力强、可靠性强、运算速度快、使用方便等优点,而且整个分析过程也是一次完成,大大简化了计算工作量。
2 温控参数有限元法的基本原理
2.1 抗剪强度的折减
为了使边坡达到极限状态,需要对内聚力、摩擦角和膨胀角分别按式(1)进行折减。采用有效应力指标,

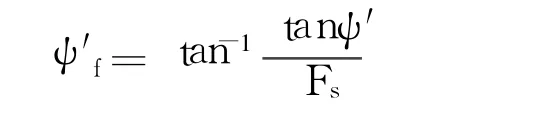
其中,c′f、φ′f和 ψ′f分别为折减 Fs倍后的有效内聚力、摩擦角和膨胀角。按照前述方法确定的临界折减系数 Fs,即为边坡稳定的安全系数。
对土坡强度折减的程度,即土的实际强度与极限状态时所采用强度的比值,具有强度储备的物理意义,和传统极限平衡方法是一致的。
2.2 温控参数有限元法的基本原理
传统的离散试验算法是强度参数不随时步变化,每一组试验参数都要进行一个完整的时步计算。显然,要找出一个使边坡刚好达到极限状态的 Fs是比较繁琐的。而在 ABAQUS程序中,可以利用其现成的材料参数随温度场变量的变化而变化的功能,定义材料强度指标随着温度场的变化而变化。此温度场只是一个变量场,不代表真实温度,只起到带动材料参数变化的作用。如果给定其热膨胀系数为 0,那么温度变化不会给结构带来应力和变形上的变化。
对于安全系数在 1.0~10.0之间的一般情况,当温度场变量 θ由 0增加到 100时,定义 c′f和 tanφ′f随着 θ线性折减到 0.1c′f和 0.1tanφ′f,即 1/Fs由 1.0折减到 0.1。其数学关系式为:

静力分析中的时步不代表真实时间,只代表“载荷”的变化过程。当 t由 0增加到 1.0时,定义温度场 θ随时步 t由 0线性增加到 100。即

把式(3)代入式(2),从而得出安全系数 Fs和时步 t之间关系:

这样,通过递推,实现了材料强度参数与时步t的一一对应,并随着 t的增加而线性折减。对于安全系数小于 1.0的情况也可以采用同样的方法,只要增大 1/Fs的值即可。
计算分两步进行,在第一步中,采用土体的真实强度参数模拟整个加载过程;在第二步中,控制温度场随时步的增加而变化,从而带动强度参数不断折减。在每一时步,考察该时刻对应的强度参数下每一点的应力状态,与破坏准则相比较。如果某一点上的应力位于屈服面内,则认为该点处于弹性响应,如果应力位于屈服面上,则按照弹塑性理论,将屈服应力在单元中重分配。若计算收敛,则时步自动增加一个 △t,强度参数折减到t+△t时刻对应的值,继续计算该时刻的应力和变形;若计算不收敛,则减少增量步再次迭代。但这个求解过程,都是由 ABAQUS自动完成的,无需重新编制程序或人为干预计算过程。
3 屈服准则和极限状态判据
这表示边坡变形突变,达到极限状态。如果δmax/H大于 0.1,则做出 δmax/H~ t关系曲线,找出 δmax/H位于 0.05~0.1之间且其值突变时刻对应的 Fs作为安全系数。此时,边坡变形急剧增加,Fs差别甚小。这一土坡破坏标准便于数值计算,避免采用不收敛作为破坏标准可能导致结果偏大或者偏小的缺点。
在边坡稳定分析中,采用不同的屈服准则,往往也会使计算结果有较大的差异。采用外接圆的Duncker-Prager模型,得到的安全系数比传统结算结果大 25%左右[3]。本文采用岩土工程中广泛采用的 Mohr-Coulomb准则,大量的工程实践证明了该准则的精度和可靠性。
为了与采用圆弧滑裂面进行极限平衡分析的经典算例进行比较,本文采用膨胀角为 0的非关联流动法则进行有限元计算。
另一方面,不同研究者对极限状态的确定是不相同的。有的认为计算不收敛便是极限状态[3~5],或者以一定迭代次数作为极限状态的判定准则[6]。此外还有人把塑性区的连通看成是达到了极限状态[7],或者以边坡体内某一幅值的广义剪应变从边坡底部下方向坡顶上方贯通作为极限状态的标志[8]。但是,不同的收敛准则或不同的迭代方法可能导致不同的计算结果,需要加以考察。
采用有限元程序进行计算,有时边坡变形甚至大于坡高,计算仍收敛;有时边坡几乎没有变形,计算已经不收敛。如果按照通常的计算不收敛作为判断标准,肯定会有很大的误差。本文针对通用有限元软件 ABAQUS,采用四节点的四边形单元进行计算。考察无量纲位移 δmax/H与时步 t的关系,其中 δmax为边坡体的最大节点位移,H为边坡高度。通过以下两个算例发现,当 t大于某一数值后,δmax/H会快速增长,并导致程序不收敛而中止计算。
不收敛时刻 t并不能直接代入式(4)来确定安全系数。根据分析问题和采用控制条件的不同,不收敛时 δmax/H值的范围是不同的。δmax/H可能大于 0.1,可以判断为边坡已经破坏,只是由于采用单元类型的数值稳定性和程序极强的非线性计算功能而继续计算。也可能 δmax/H小于0.05,说明边坡变形还没有突变,可能是模型或控制条件不当导致程序提前不收敛。只有当不收敛时对应的 δmax/H在 0.05~0.1之间时,才可把不收敛时刻 t代入式(4)来确定安全系数 Fs,因为
4 算例分析
4.1 均质土坡的安全系数
土坡几何模型及四边形单元网格划分如图 1所示,坡高 20m,坡度 1∶2,右边界距坡趾和左边界距坡顶均为 40m,底边界距坡底 10m。材料参数:E=100MPa,ν=0.3,γ=20kN/m3,c=20kPa,φ=20°。基底采用刚性边界,两侧为水平约束,上部边界为自由边界。

图 1 均质土坡的有限元网格
图 2给出无量纲位移 δmax/H与时步 t的关系。取 δmax/H急剧增大,且其值位于 0.05~0.1之间时,对应的强度折减系数作为边坡整体的稳定系数,可以取 t=0.3115,对应 δmax/H=0.05,安全系数 Fs=1.390。
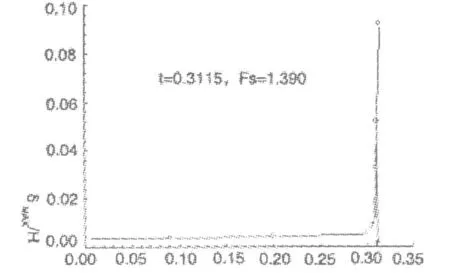
图 2 无量纲位移与时步t的关系
图 3(a)和图 3(b)对应于极限状态 Fs=1.390时节点位移矢量和变形网格。由位移场和变形场的分布情况判断,这种判定准则是合理的。对于给定的问题,所得到的有限元数值解与 Bishop和 Morgenstern的极限平衡解 Fs=1.380、Grif-fiths和 Lame的有限元数值解 Fs=1.4都很接近[5]。这种确定安全系数的方法避免了目前采用数值计算不收敛作为判断标准的人为不确定性。事实上,由于 ABAQUS的非线性计算能力很强,本算例在 t=0.335时候才开始不收敛。如果按照计算不收敛作为判断标准,安全系数 Fs=1.432,对应的 δmax/H=2.0,边坡已经破坏。

图 3 对应于Fs=1.390的网格变形图(a)节点位移矢量;(b)变形网格
4.2 非均质土坡的安全系数
本例来源于澳大利亚计算机应用协会(ACADS)的一个考题[9],几何模型和材料分区如图 4所示,材料特性如表 1所示。

图 4 非均质边坡的几何模型

表 1 各土层的强度参数指标
图 5给出无量纲位移 δmax/H与时步 t的关系,可以得出当 t=0.304时达到极限状态,对应的 δmax/H=0.08,安全系数 Fs=1.377。这与推荐的裁判答案 Fs=1.39误差 1%。此例收敛于 t=0.304,δmax/H=0.08,位于 0.05 ~ 0.1之间 ,可以直接采用计算不收敛作为判断标准。
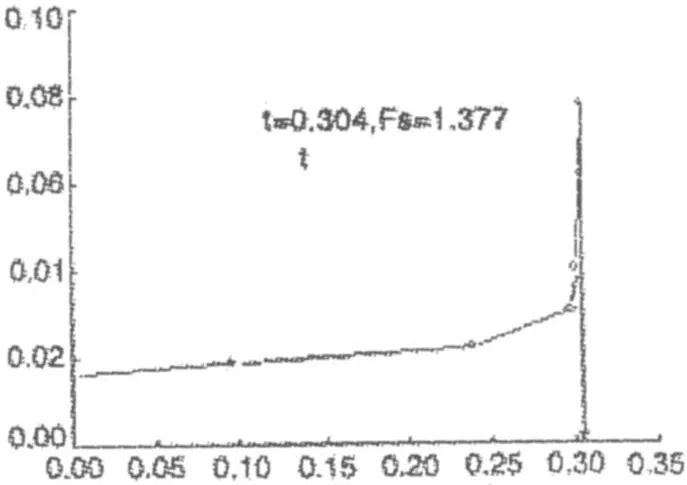
图 5 无量纲位移与时步t的关系
5 结语
在 ABAQUS程序中,采用温控参数法来计算边坡的稳定安全系数,不仅能最大限度地利用ABAQUS本身所具有的计算精度高、非线性求解能力强、可靠性强、运算速度快、使用方便等优点,而且不用另外编制程序,整个分析过程也是一次完成的,大大简化了计算工作量。
本文通过两个算例,得出取 δmax/H在 0.05~0.1之间时,对应的 Fs作为整体安全系数这一土坡破坏标准,便于数值计算,避免采用不收敛作为破坏标准的缺点。
〔1〕程 晔,赵明华,曹文贵.基桩下溶洞顶板稳定性评价的强度折减有限元法[J].岩土工程学报,2005,27(1):38~41.
〔2〕宋二祥,高 翔,邱 玥.基坑土钉支护安全系数的强度参数折减有限元方法[J].岩土工程学报,2005,27(3):258~263.
〔3〕郑颖人,赵尚毅.岩土工程极限分析有限元法及其应用[J].土木工程学报,2005,38(1):91~98.
〔4〕Dawson E M,Roth W H,Drescher A.Slope stability analysis by strength reduction[J].Geotechnique,1999,49(6):835~840.
〔5〕Griffiths D V,Lame P A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3):387~403.
〔6〕Ugai K.A method of calculation of total factor of safety of slopes by elasto-plastic FEM[J].Soils and Foundations,1989.29(2):190~195.
〔7〕栾茂田,武亚军,年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23(3):1~8.
〔8〕连镇营,韩国城,孔宪京.强度折减法研究开挖边坡的稳定性[J].岩土工程学报,2001,23(4):406~411.
〔9〕陈祖煜.土质边坡稳定分析:原理·方法·程序[M].北京:中国水利水电出版社,2003.

