扩散角对汽车风洞扩散段流动的影响

杨志刚,周晓利 ,李启良 ,贾 青

(同济大学上海地面交通工具风洞中心,上海 201804)

0 引 言

整车风洞是汽车空气动力学试验研究不可缺少的试验设施。为了满足中国汽车工业的需要,包括全尺寸气动-声学风洞和热环境风洞的上海地面交通工具中心已于2009年9月落成并投入使用[1]。扩散段是汽车风洞的一个关键部件,位于试验段下游,将来自试验段气流逐渐减速,使气流的动能转化为势能,减少气流在下游各管段的压力损失,降低风洞所需的功率。扩散段流动是一种复杂的流动,在满足扩散段进出口面积比条件下,进口截面速度不均匀度和扩散角对扩散段流动特性有很大的影响。研究它们对汽车风洞扩散段流动的影响,不仅可以深入了解扩散段的流动状态,而且有利于指导汽车风洞扩散段的设计。

扩散段的流动形态在过去的一段时间里进行了相关的试验和数值研究。C.U.Buice et al[2]从试验角度研究了均匀来流下,矩形截面对称扩散段的流动特性。P.A.Durbin[3]使用v2f湍流模型对均匀来流下,2D扩散段进行数值模拟发现,使用该模型能够得到与试验相一致的结果。过去的研究描述了均匀来流下,扩散段的流动形态。然而,非均匀来流下的扩散段流动形态仍未涉及。传统航空风洞多数为闭口式风洞,风洞试验段的出口速度相当均匀。对于试验段下游的扩散段的设计,往往采用基于均匀来流条件下得到的经验公式和图表[4]。然而,汽车风洞通常采用开口式风洞,喷口与收集口截面不同,试验段的出口速度不均匀,如果仍采用传统的设计,可能会带来严重的偏差,增加风洞设计风险。

为此,首先针对模型风洞扩散段流动形态展开数值与试验研究,然后使用数值方法对一系列扩散角的扩散段流动进行模拟,以求在更接近扩散段真实运行条件下寻找到压力损失因数与扩散角的关系,为汽车风洞扩散段的设计提供指导。

1 试验与数值模拟方法

1.1 试验方法

为了研究汽车风洞空气动力学性能,建设1∶15的模型风洞,如图1所示。模型风洞速度由电机控制,其最大出口风速为45m/s。考虑到模型风洞运行和传感器量程等因素,选取35m/s的出口风速进行试验。试验使用皮托管对收集口进口和扩散段出口截面进行多点压力测量,通过总压和静压换算得到测试截面速度分布。收集口进口的速度分布的试验结果主要用来验证扩散段计算给定进口边界条件的合理性,距扩散段出口约210mm处的速度分布的试验结果,则主要用于评估计算得到扩散段流场的正确与否。

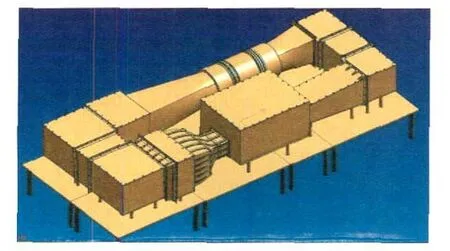
图1 模型风洞示意图Fig.1 Schematic of model wind tunnel

尽管15°的收集口角度所对应试验段流场质量较好[5],但是出于以往研究均将收集口角度为0°作为基础状态,故在试验与数值模拟中均对收集口角度为0°时扩散段的流动形态进行分析。计算区域进口的两种非均匀来流主要通过在试验段天平位置是否放置车模来实现。

1.2 数值模拟方法

在数值模拟中,仅选取模型风洞的一部分。整个计算区域由收集口、扩散段以及为了防止回流而添加的延伸段组成,如图2所示。之所以在扩散段后面直接添加延伸段而不是连接拐角1,是因为两者对扩散段内流动形态和总压损失影响不大。计算区域内的流场使用商业软件Gambit进行网格划分。考虑到v2f湍流模型对壁面网格的要求,在壁面创建边界层网格,使近壁面网格y+≈5。整个计算区域均创建能有效减少数值扩散、提高求解精度的六面体网格,其网格总数约为222万个。其它扩散角下的网格创建方式与此相同,由于扩散角越大,扩散段对应的表面积越小,因而由此导致最终生成的体网格数目减少,在计算的所有扩散段中,网格总数处于108～222万个。

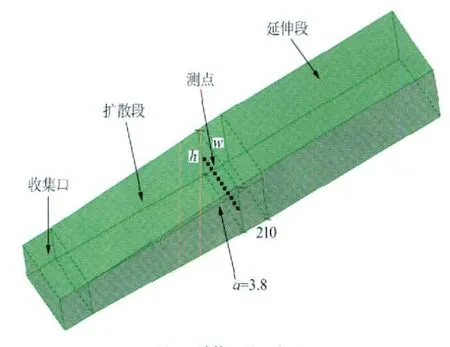
图2 计算区域示意图Fig.2 Schematic of computational domain

基于有限体积法的商业软件Fluent框架下的v2f湍流模型用于不同扩散角下扩散段的湍流场求解。v2f湍流模型在标准k-e湍流模型基础上,考虑垂直于流线方向的速度脉动,采用可以代表近壁面湍流输运方程中阻尼的合适尺度的速度尺度v2方程,同时在近壁面处理上利用椭圆松驰法构造 f函数[3]。v2f湍流模型解决了壁面附近湍流的各项异性问题,可以准确地模拟边界层的分离、再附、或以分离为主的流场[6]。

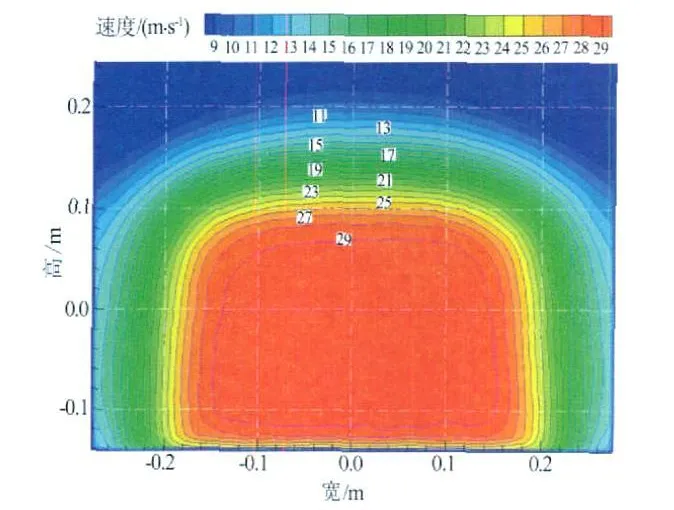
图3 计算域进口速度分布(试验段无车)Fig.3 Velocity distribution of computational domain inlet(test section without car)

计算区域的进口使用非均匀速度分布,如图3所示。该速度分布是通过对整个模型风洞进行计算得到的,并且该速度分布得到了试验验证[7]。从图3可以看出,计算区域的进口速度分布非常不均匀,计算得到的速度不均匀度可达50.5%。这将是汽车风洞与航空风洞的最大区别之一。因为对于航空风洞扩散段的进口速度分布相当均匀,但汽车风洞扩散段进口却是如此不均匀。计算区域的出口使用压力出口,收集口和扩散段壁面采用无滑移条件,延伸段采用无粘壁面条件。计算首先采用较为稳定的1阶迎风格式,几百次乃至上千次迭代后,选用精度较高的2阶迎风格式,直到残差收敛至10-4,且监控物理量的数值基本不随迭代发生改变时,则认为计算收敛。

2 结果分析与讨论

2.1 数值结果与试验结果对比

在图2给出的测试截面中,原点位于截面中心,高度方向上布置8排,每排有11个测点。图4仅给出出口速度为35m/s、高度方向z=-35mm的两种非均匀来流下扩散段的无量纲速度分布。从图中的试验结果可以看出,扩散段从两侧无量纲速度约0.6增加到中心无量纲速度约1.3,且呈现出对称分布。应该指出的是,图4的u进指的是扩散段进口的平均速度,观察图3给出的速度分布可以判断出扩散段内无量纲速度分布可以超过1.0。受出口射流的影响,即使到了扩散段入口截面,轴心速度降低较少。从图4试验给出的速度分布可以反映出,扩散段有助于降低射流轴心速度,约降低30%,并使速度不均匀度从进口的33.9%降低到出口的26.9%,但它并没有完全消除出口射流影响。从两种非均匀来流下的数值与试验结果可以看出,不仅它们变化趋势一致,而且大多数测点上的速度值也基本相同。计算两者平均速度发现,数值模拟得到的速度为13.4m/s,试验测量得到的速度为13.7m/s,误差约为2.2%。可见,数值模拟能真实反映扩散段流场的分布。

2.2 总压损失因数

总压损失因数是评价风洞扩散段气动性能的主要参数,其定义如式(1)所示。

式中,Δ Cp表示总压损失因数;Δ Pt表示扩散段进口与计算区域出口的总压差(Pa);ρ表示密度(kg/m3)。

2.2.1 来流速度不均匀度

为了考察来流速度不均匀度对扩散段总压损失的影响,选取模型风洞扩散段在各种工况下的计算结果进行对比,如表1所示。从表中可以看出,随着来流的速度不均匀度增加,扩散段总压损失因数不断增加,且增幅较大。试验段中无车对应扩散段总压损失因数约为均匀来流时的5.2倍,可见在风洞扩散段设计时,仅依赖均匀来流得到的结果来设计,往往出现严重的偏差。比较两种非均匀来流工况下,扩散段总压损失因数发现,由于速度不均匀度的减少,相同扩散角下,有车对应扩散段总压损失因数比无车要小。

表1 各来流情况下,扩散段总压损失因数T able 1 Total pressure factor of diffuser under different inflows

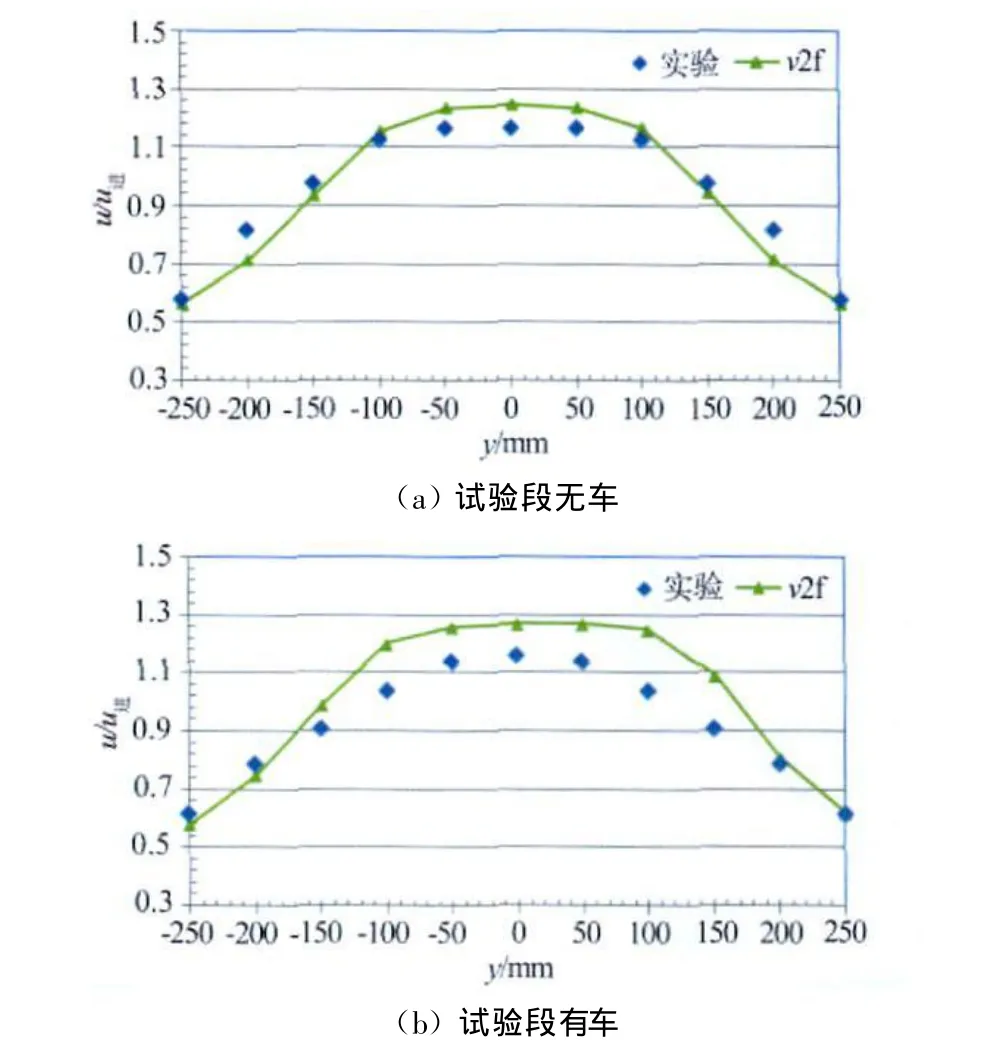
图4 扩散段无量纲速度分布Fig.4 Dimensionless velocity distribution of diffuser

2.2.2 扩散角

两种非均匀来流工况下,扩散段总压损失因数与扩散角的变化,如图5所示。从图中可以看出,随着扩散角的增加,扩散段总压损失因数先减少后增加,呈现出V型的变化趋势。当来流处于试验段有车工况时,扩散段总压损失因数最小值对应扩散角为13.0°。当来流处于试验段无车工况时,扩散段总压损失因数最小值对应扩散角为14.5°。

扩散段的总压损失由壁面摩擦损失和流动分离损失组成。对照图5无车曲线可知,当扩散角从3.8°到14.5°,壁面摩擦损失由于扩散角增加导致壁面面积减少而不断减少,流动分离损失由于扩散角增加而不断增加。然而,从该曲线变化趋势可知壁面摩擦损失减少起决定性作用。当扩散角大于14.5°,流动分离损失增加起决定性作用。图6显示试验段无车时两种扩散角下扩散段分离情况。由于扩散段进口速度非均匀分布,即使扩散段处于较小的扩散角,较小的逆压梯度也会使扩散段顶部和侧壁交界处出现流动分离。流动分离随着扩散角增加而急剧增大。当扩散角为14.5°时,在扩散段的四个壁面交界处出现不同程度的流动分离,其中顶部分离较大,底部分离较小。这显然是由于进口速度分布导致的。可见,随着扩散角增加,分离加剧,由流动分离带来损失不断增加。至于试验段有车时,扩散段流动分离情况与此类似,不予叙述。

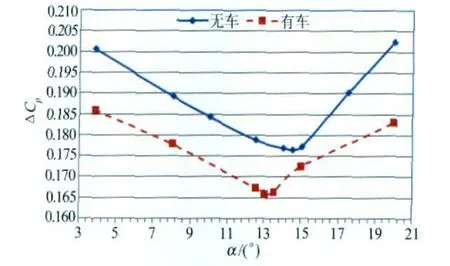
图5 不同扩散角下,扩散段总压损失因数Fig.5 Total pressure factor of diffuser under different diffuser angles

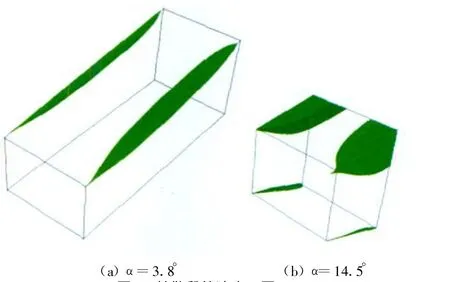
图6 扩散段等速度云图(u=0m/s)Fig.6 Iso-surface contour of diffuser(u=0m/s)

3 结论与展望

模型风洞扩散段出口速度分布的数值模拟与实验结果相吻合表明,v2f湍流模型不仅可以较好模拟均匀来流下扩散段流动,而且可以较真实反映出非均匀来流下扩散段流动情况。

来流速度分布影响着扩散段总压损失,来流速度不均匀度越大,扩散段总压损失越大。试验段无车时,扩散段总压损失因数是均匀来流时的5.2倍。风洞扩散段设计使用均匀来流得到的经验公式或图表将会带来较大偏差。

对于扩散段,总存在一个最优扩散角,其也受来流速度不均匀度影响。来流速度不均匀度越大,最佳扩散角越大。

[1] YANG Z.Shanghai automotive wind tunnel center project[C].Proc.Stuttgart Symposium,2007.

[2] BUICE C U,EATON J K.Experimental investigation of flow through an asymmetric plane diffuser[J].Journal of Fluid Engineering,2000,122(2)：433-435.

[3] DURBIN P A.Separated flow computations with the ke-v2 model[J].AIAA Journal,1995,33(4)：659-664.

[4] 刘政崇.高低速风洞气动与结构设计[M].北京：国防工业出版社,2003.

[5] 李启良,郑志强,贾青,等.两种改善汽车风洞轴向静压系数的方法[J].同济大学学报(自然科学版),2010,38(3)：26-30.

[6] GIANLUCA I.Prediction of the turbulent flow in a diffuser with commercial CFD codes[R].Center for Turbulence Research Annual Research Briefs,2000：271-278.

[7] 李启良,杨志刚.计算流体力学在气动-声学风洞设计中的应用[J].空气动力学学报,2009,27(3)：373-377.